Точки перегиба

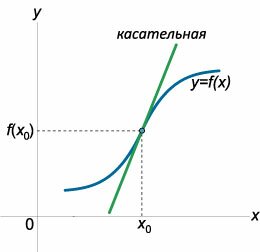
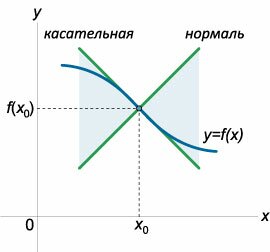
Рассмотрим функцию y = f(x), которая является непрерывной в точке x₀. Функция f(x) может иметь в этой точке конечную или бесконечную производную f '(x₀). Если при переходе через x₀ функция меняет направление выпуклости, т.е. существует число δ > 0, такое, что на одном из интервалов (x₀ − δ, x₀) или (x₀, x₀ + δ) функция является выпуклой вверх, а на другом − выпуклой вниз, то x₀ называется точкой перегиба функции y = f(x).

Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются (рисунок 1).

Другое интересное свойство точки перегиба состоит в том, что график функции f(x) в окрестности точки перегиба x₀ расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок 2). Если x₀ − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки x₀, причем в точке x₀ она непрерывна, то Доказательство.
Предположим, что в точке перегиба x₀ вторая производная не равна нулю:  f ''(x₀) ≠ 0. Поскольку она непрерывна при x₀, то существует δ-окрестность точки x₀, в которой вторая производная сохраняет свой знак, т.е. В таком случае функция будет либо строго выпукла вверх (при  f ''(x) < 0), либо строго выпукла вниз (при f ''(x) > 0). Но тогда точка x₀ не является точкой перегиба. Следовательно, предположение неверно и вторая производная в точке перегиба должна быть равна нулю. Если функция f(x) непрерывна и дифференцируема в точке x₀, имеет вторую производную f ''(x) в некоторой проколотой δ-окрестности точки x₀ и если вторая производная меняет знак при переходе через точку x₀, то x₀ является точкой перегиба функции f(x).

Доказательство.
Пусть, например, вторая производная  f ''(x) при переходе через точку x₀ меняет знак с плюса на минус. Следовательно, в левой δ-окрестности (x₀ − δ, x₀) выполняется неравенство  f ''(x) > 0, а в правой δ-окрестности (x₀, x₀ + δ) справедливо неравенство  f ''(x) < 0.

В таком случае, согласно достаточным условиям выпуклости, функция f(x) выпукла вниз в левой δ-окрестности точки x₀ и выпукла вверх в правой δ-окрестности.

Следовательно, в точке x₀ функция меняет направление выпуклости, т.е. x₀ является, по определению, точкой перегиба. Пусть  f ''(x₀) = 0,  f '''(x₀) ≠ 0. Тогда точка x₀ является точкой перегиба функции f(x).

Доказательство.
Поскольку  f '''(x₀) ≠ 0, то вторая производная в точке x₀ либо строго возрастает (если  f '''(x₀) > 0), либо строго убывает (если  f '''(x₀) < 0). Так как  f ''(x₀) = 0, то вторая производная при некотором δ > 0 имеет разные знаки в левой и правой δ-окрестности точки x₀. Отсюда, на основании предыдущей теоремы, следует что x₀ − точка перегиба функции f(x).

   Пример 1

Выяснить, является ли точка x = 0 точкой перегиба функции  f(x) = sin x. Воспользуемся вторым достаточным признаком существования точки перегиба. Найдем производные синуса до третьего порядка включительно: В точке x = 0 вторая и третья производные имеют следующие значения: Таким образом, имеем  f ''(0) = 0,  f '''(0) ≠ 0. Следовательно, по второму достаточному признаку точка x = 0 является точкой перегиба.

   Пример 2

Найти точки перегиба функции Находим производные: Вычисляем корни второй производной: В данном случае удобно использовать второй достаточный признак существования точки перегиба. Третья производная записывается в виде Отсюда сразу видно, что в точках  x₁ = 2,  x₂ = 4  третья производная не равна нулю. Следовательно, эти точки будут являться точками перегиба.

   Пример 3

Найти точки перегиба функции  f(x) = x² ln x. Находим вторую производную: Решаем уравнение  f ''(x) = 0: Вторая производная представляет собой монотонно возрастающую функцию. Поэтому в найденной точке происходит смена знака второй производной. Следовательно, эта точка является точкой перегиба.

   Пример 4

Найти точки перегиба функции  f(x) = e^−x2 . Вычислим производные: Вторая производная равна нулю в следующих точках: При переходе через точки  x₁ = −1/√2,  x₁ = 1/√2 вторая производная меняет знак (рисунок 3). Следовательно, указанные точки являются точками перегиба.

   Пример 5

Найти точки перегиба функции  f(x) = e<sup>sin x. Определим производные заданной функции: Точки перегиба должны удовлетворять уравнению  f ''(x) = 0. Тогда Данное тригонометрическое уравнение из школьного курса математики решается с помощью замены sin x = t. Следовательно, Первый корень t₁ со знаком минус в числителе нужно отбросить, поскольку t₁ < −1. Тогда уравнение имеет следующее единственное решение: Итак, мы получили бесконечное множество точек, в которых вторая производная функции равна нулю. В пределах отрезка [0, 2π] существуют два решения, равные Остальные решения x_n образуются вследствие периодичности синуса и, следовательно, всей функции f(x).

Оба решения x₁ и x₂ соответствуют правому корню квадратного уравнения. Ясно, что при пересечении корня (в случае двух различных действительных корней) квадратичная функция меняет знак. Поэтому вторая производная, имеющая вид также меняет знак при переходе через точки x_n. Отсюда, в соответствии с первым достаточным признаком, вытекает, что все найденные точки x_n являются точками перегиба. Схематический вид функции на отрезке [0, 2π] показан на рисунке 4.</sup>

   Пример 6

При каких значениях a и b точка (−1, 2) является точкой перегиба графика функции  y(x) = ax³ + bx² ? Первая и вторая производные заданной кубической функции выражаются формулами: В точке перегиба вторая производная равна нулю, т.е. первое уравнение имеет вид: Вторым уравнением служит уравнение самой функции. В результате получаем следующую систему для определения a и b: Подставим известные координаты точки перегиба графика функции: Убедимся с помощью второго достаточного признака, что точка перегиба определена корректно. Проверим, что третья производная не равна нулю: Следовательно, заданная точка (−1, 2) является точкой перегиба графика функции  y(x) = −x³ + 2x².

   Пример 7

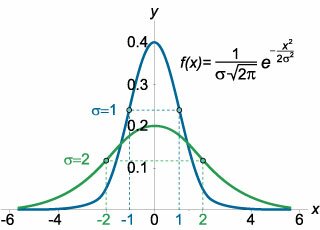
Найти точки перегиба функции Гаусса. Функция Гаусса или функция плотности нормального распределения определяется формулой где μ − математическое ожидание, σ − среднеквадратичное отклонение распределения. Далее будем считать, что μ = 0. Вычислим первую производную: Продолжая дифференцирование, находим вторую производную: Корни второй производной равны Поскольку знак второй производной определяется квадратичным выражением  x² − σ², то ясно, что при переходе через точки x = ±σ вторая производная будет менять свой знак. Поэтому, в соответствии с первым достаточным признаком, точки x = ±σ являются точками перегиба. Схематический вид функции Гаусса при σ = 1 и σ = 2 приведен на рисунке 5.

   Пример 8

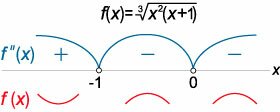
Найти точки перегиба функции Вычислим сначала первую производную: Продолжая дифференцирование, определяем вторую производную: Видно, что вторая производная нигде не равна нулю. Однако точки перегиба могут быть при  x = −1  и  x = 0 , где знаменатель равен нулю и вторая производная не существует. Исследуем знак второй производной при переходе через эти точки (рисунок 6).

Таким образом, при переходе через точку  x = −1  вторая производная меняет знак с плюса на минус. Следовательно, эта точка является точкой перегиба. Другая точка  x = 0  не является точкой перегиба, поскольку в ее окрестности знак второй производной не меняется.

   Пример 9

Найти точки перегиба кривой, заданной параметрически: Первая производная y_x'  параметрической функции определяется по формуле Подставляя заданные выражения x(t), y(t), получаем: Аналогично находится вторая производная  y_x'': Найдем значения параметра t, при которых вторая производная равна нулю: Чтобы выяснить, соответствуют ли найденные значения t₁, t₂ точкам перегиба, вычислим третью производную (то есть применим второй достаточный признак существования точки перегиба): При подстановке значений  t_1,2 = ±1/√3  третья производная на равна нулю. Поэтому, согласно второму достаточному признаку, кривая имеет точки перегиба при  t_1,2 = ±1/√3.

Вычислим координаты x и y точек перегиба: На рисунке 7 схематически показана заданная кривая и отмечены ее точки перегиба. Как видно, она состоит из двух ветвей, симметричных относительно оси 0x.

   Пример 10

Показать, что график функции имеет три точки перегиба, лежащие на одной прямой. Следуя общей схеме, найдем последовательно первую и вторую производную: Кубический многочлен в числителе раскладывается следующим образом: Разложим также квадратичную функцию на множители: Следовательно, вторая производная исходной функции записывается как Таким образом, вторая производная имеет три корня: причем при переходе через каждую из этих точек вторая производная меняет знак, то есть найденные точки являются точками перегиба.

Вычислим соответствующие значения y: Итак, точки перегиба графика функции имеют такие координаты: Убедимся, что эти три точки лежат на одной прямой. В этом случае должно выполняться пропорциональное соотношение Подставляем найденные координаты: Это доказывает, что точки перегиба расположены на одной прямой. Схематически график функции показан на рисунке 8.