|
Производные высшего порядка
|
|
Производные высшего порядка явно заданной функции
Пусть функция y = f(x) имеет конечную производную f '(x) в некотором интервале (a, b), т.е. производная f '(x) также является функцией в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции f, которая обозначается в виде
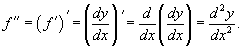 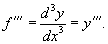 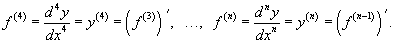 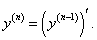 Отметим, что для нахождения производных высшего порядка можно использовать следующие линейные соотношения: 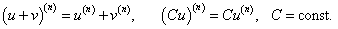
Производные высшего порядка неявно заданной функции
Производная n-го порядка неявно заданной функции находится последовательным (n раз) дифференцированием уравнения F(x, y) = 0. На каждом шаге, после соответствующих подстановок и преобразований, можно получить явное выражение для производной, зависящее лишь от переменных x, y, т.е. производные имеют вид
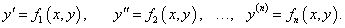
Производные высшего порядка функции, заданной параметрически
Рассмотрим функцию y = f(x), заданную параметрически с помощью двух уравнений
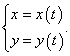 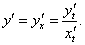 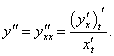 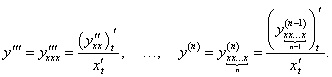 |
|
Пример 1
|
|
Найти
Решение. 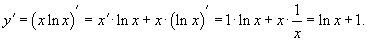 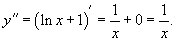 |
|
Пример 2
|
|
Найти вторую производную функции
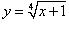 . .
Решение. 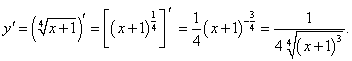 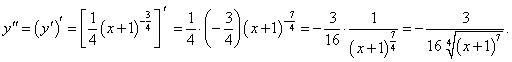 |
|
Пример 3
|
|
Вычислить
Решение. 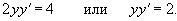 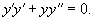 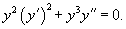 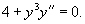 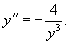 |
|
Пример 4
|
|
Дана функция y = (2x + 1)3(x − 1). Найти все производные n-го порядка с n = 1 до n = 5.
Решение. 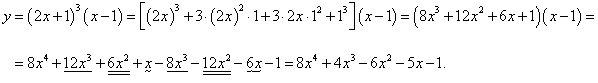 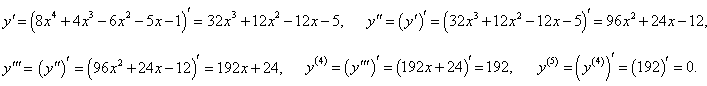 |
|
Пример 5
|
|
Найти производную n-го порядка функции натурального логарифма y = ln x.
Решение. 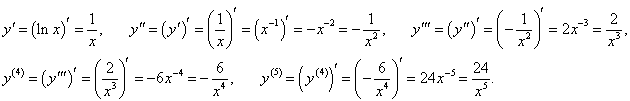 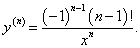 |
|
Пример 6
|
|
Определить все производные синуса.
Решение. 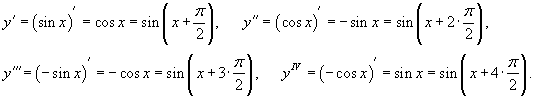 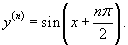 |
|
Пример 7
|
|
Определить все производные косинуса.
Решение. 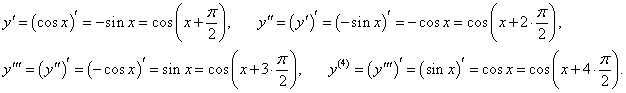 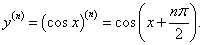 |
|
Пример 8
|
|
Найти все производные функции
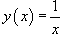 . .
Решение. 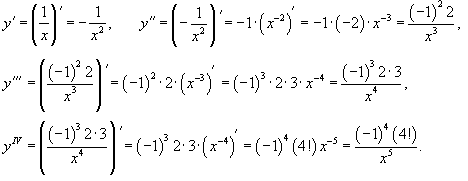 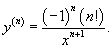 |
|
Пример 9
|
|
Найти вторую производную функции
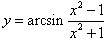 . .
Решение. 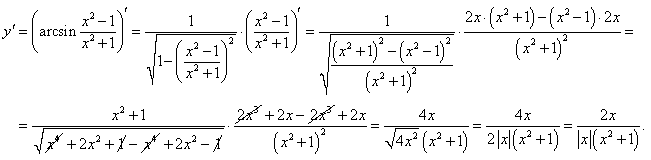 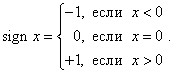 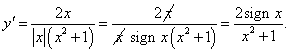 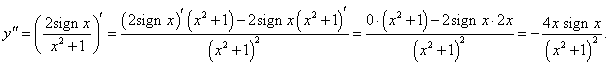 |
|
Пример 10
|
|
Найти третью производную функции
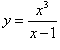 . .
Решение. 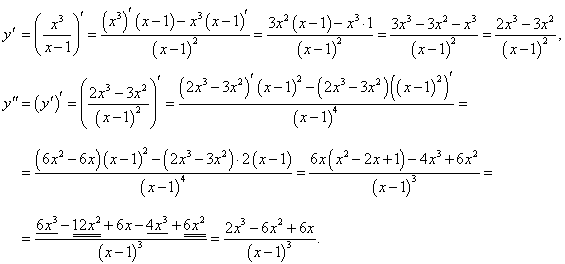 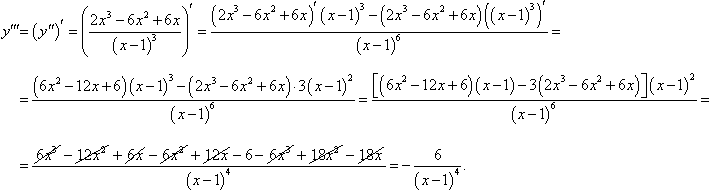 |
|
Пример 11
|
|
Найти вторую производную неявно заданной функции x2 + y2 = R2 (каноническое уравнение окружности).
Решение. 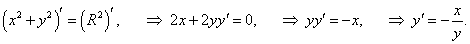 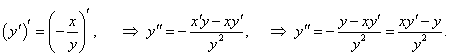 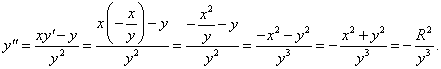 |
|
Пример 12
|
|
Найти производную n-го порядка функции y = 32x+1.
Решение. 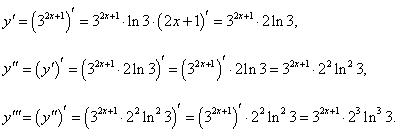 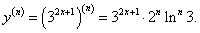 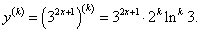 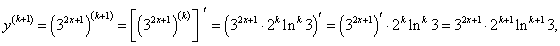 |
|
Пример 13
|
|
Найти производную n-го порядка степенной функции y = xm, где m − действительное число.
Решение. 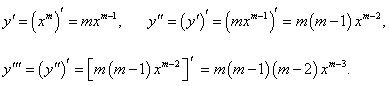 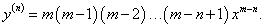 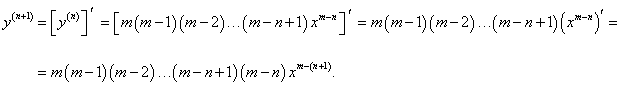 Заметим, что показатель степени m, вообще говоря, является действительным числом. Если рассматривать лишь натуральные значения m, то формулу для производной можно записать в более компактном виде: 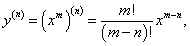 |
|
Пример 14
|
|
Найти производную n-го порядка от квадратного корня y = √x.
Решение. 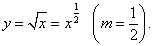 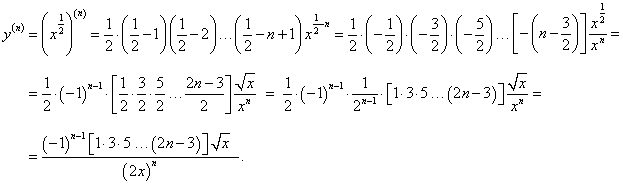 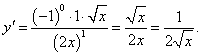 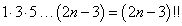 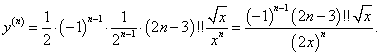 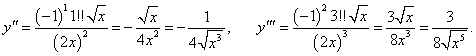 |
|
Пример 15
|
|
Найти производную n-го порядка от кубического корня
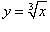 . .
Решение. 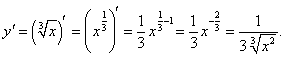 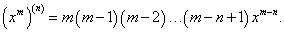 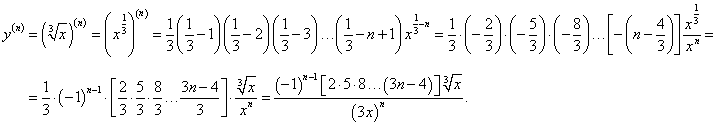 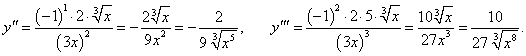 |
|
Пример 16
|
|
Найти первую и вторую производные по переменной x от функции, заданной параметрически:
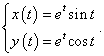 Решение. 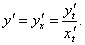 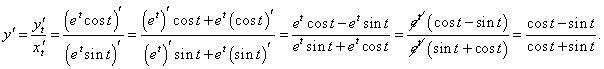 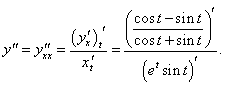 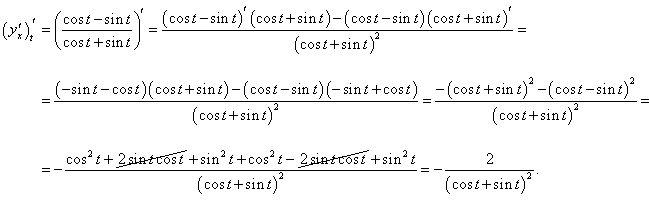 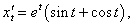 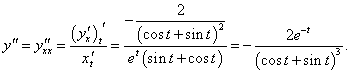 |
|
Пример 17
|
|
Дано уравнение эллипса в параметрической форме:
 Решение. 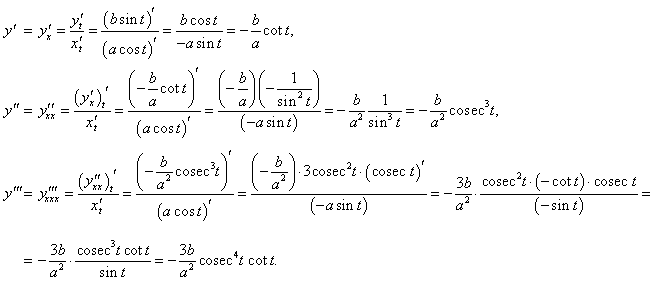 |
|
Пример 18
|
|
Найти третью производную функции, заданной уравнением x2 + 3xy + y2 = 1.
Решение. 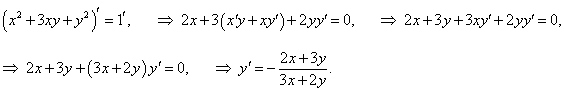 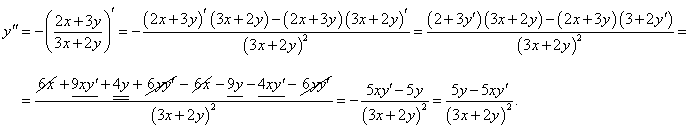 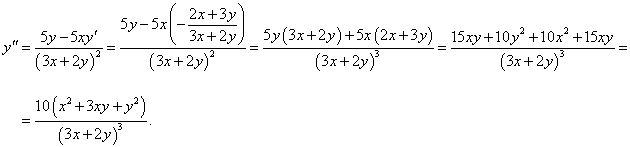 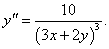 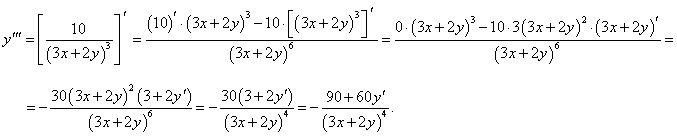 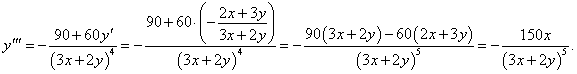 |
|
Пример 19
|
|
Найти вторую производную функции, заданной уравнением x + y = e x − y.
Решение. 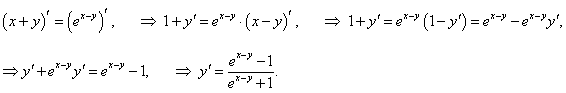 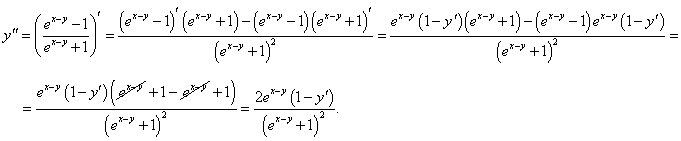 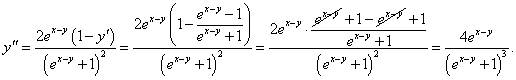 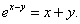 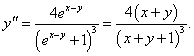 |
|
Пример 20
|
|
Кривая описывается неявным уравнением xy = 2x3 − y2 и проходит через точку (1, 1). Найти первую и вторую производные в данной точке.
Решение. 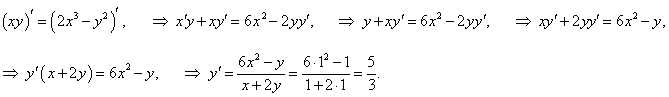 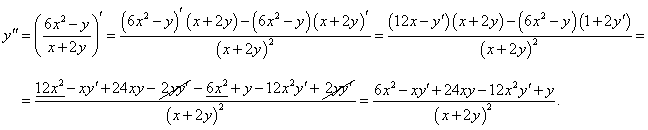 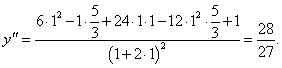 |