|
Использование интегрирующего множителя
|
|
Рассмотрим дифференциальное уравнение вида
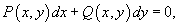 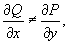 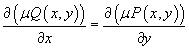 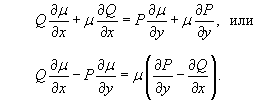 К сожалению, не существует общего метода нахождения интегрирующего множителя. Однако можно упомянуть некоторые частные случаи, для которых можно решить полученное уравнение в частных производных и, в результате, определить интегрирующий множитель.
1. Интегрирующий множитель зависит от переменной x: µ = µ (x).
В этом случае мы имеем 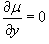 , поэтому уравнение для , поэтому уравнение для 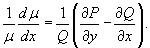
2. Интегрирующий множитель зависит от переменной y: µ = µ (y).
Аналогично, если 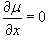 , то мы получаем обыкновенное дифференциальное уравнение, определяющее интегрирующий множитель µ: , то мы получаем обыкновенное дифференциальное уравнение, определяющее интегрирующий множитель µ:
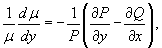
3. Интегрирующий множитель зависит от определенной комбинации переменных x и y: µ = µ (z(x,y)).
Новая функция 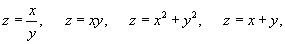 Здесь важно, что интегрирующий множитель 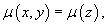 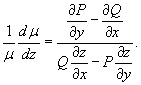 Ниже мы рассмотрим некоторые частные случаи уравнения 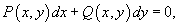 |
|
Пример 1
|
|
Решить уравнение
Решение. 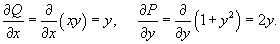 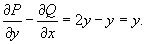 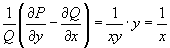 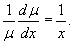 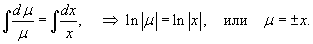 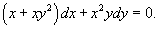 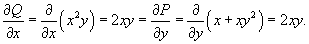 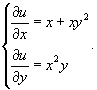 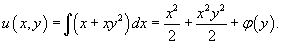 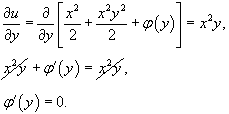 Таким образом, общее решение дифференциального уравнения определяется неявным выражением 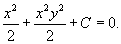 |
|
Пример 2
|
|
Решить дифференциальное уравнение
Решение. 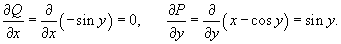 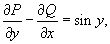 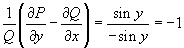 Следовательно, мы можем искать интегрирующий множитель в виде функции 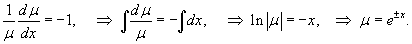 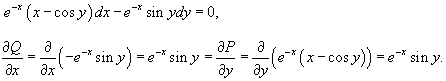 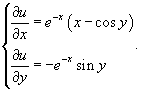 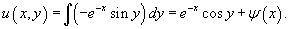 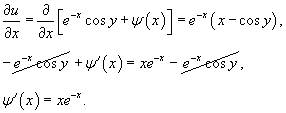 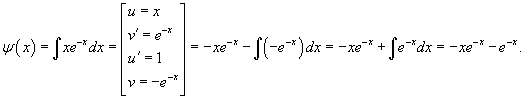 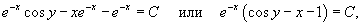 |
|
Пример 3
|
|
Решить дифференциальное уравнение
Решение. 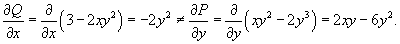 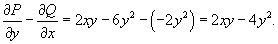 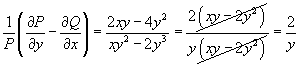 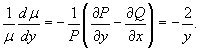 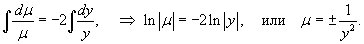 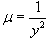 в качестве интегрирующего множителя и затем умножая на него исходное дифференциальное уравнение, получаем уравнение в полных дифференциалах: в качестве интегрирующего множителя и затем умножая на него исходное дифференциальное уравнение, получаем уравнение в полных дифференциалах:
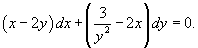 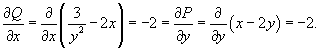 Теперь найдем функцию u из системы уравнений: 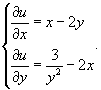 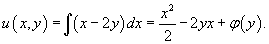 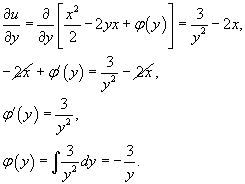 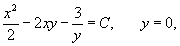 |
|
Пример 4
|
|
Решить уравнение
Решение. 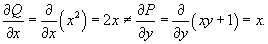 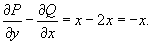 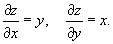 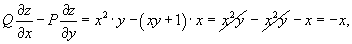 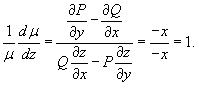 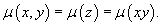 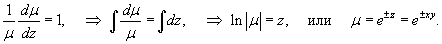 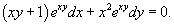 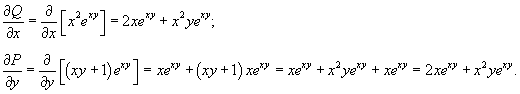 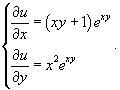 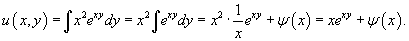 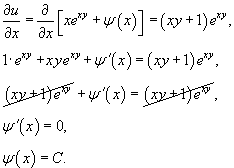 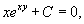 |
|
Пример 5
|
|
Решить уравнение
Решение. 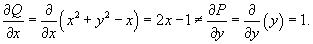 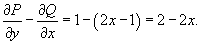 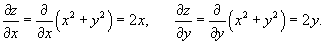 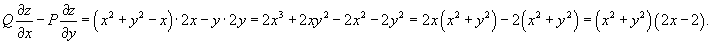 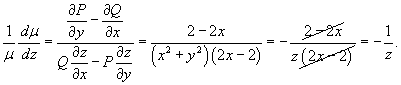 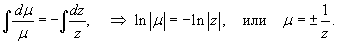 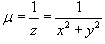 . После умножения на . После умножения на 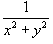 исходное дифференциальное уравнение превращается в уравнение в полных дифференциалах: исходное дифференциальное уравнение превращается в уравнение в полных дифференциалах:
 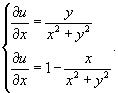 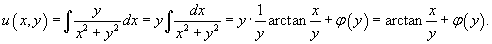 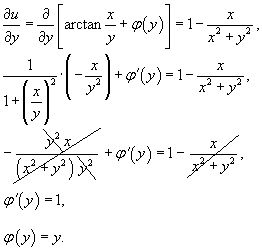 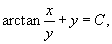 |