|
Производная обратной функции
|
|
Рассмотрим функцию
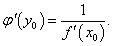 Пусть переменная y получает в точке y0 приращение 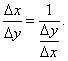 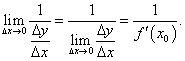 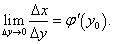 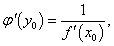 В приведенных ниже примерах найти производную заданной функции |
|
Пример 1
|
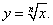
Решение.
Определим сначала обратную функцию для заданной функции 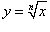 . Для этого выразим переменную x через y: . Для этого выразим переменную x через y:
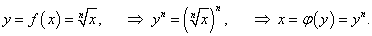 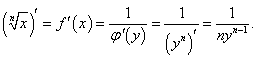 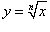 . В результате получаем выражение для производной заданной функции: . В результате получаем выражение для производной заданной функции:
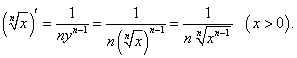 |
|
Пример 2
|
|
Решение.
Функция арксинус является обратной к функции синус. Поэтому 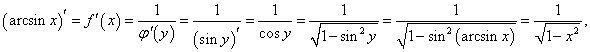 |
|
Пример 3
|
|
Решение.
Натуральный логарифм и экспоненциальная функция являются взаимно-обратными функциями. Следовательно, 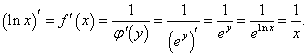 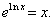 |
|
Пример 4
|
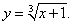
Решение.
Найдем сначала обратную функцию 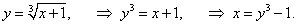 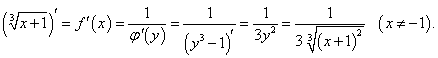 |
|
Пример 5
|
|
Решение.
Функция арккосинус определена и монотонна на отрезке 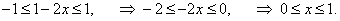 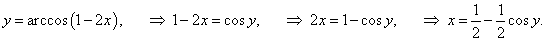 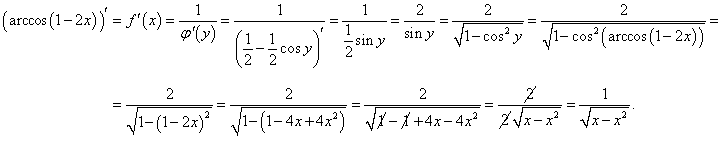 |
|
Пример 6
|
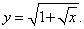
Решение.
Данная функция определена и монотонно возрастает при 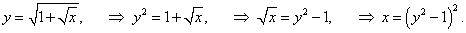 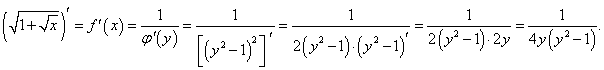 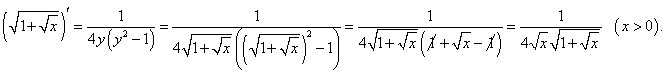 |
|
Пример 7
|

Решение.
Обратная функция для данной функции имеет такой вид:
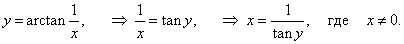 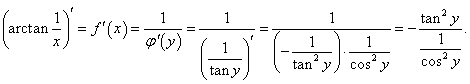 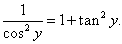 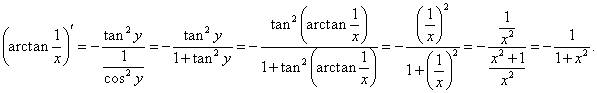 |
|
Пример 8
|
|
y = √x.
Решение.
Данная функция является обратной к квадратичной функции 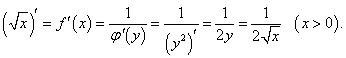 |
|
Пример 9
|
|
y = 2x + 4.
Решение.
Запишем функцию 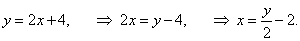 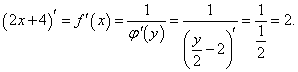 |
|
Пример 10
|
|
Дана функция y = x5 + 2x3 + 3x. Найти производную обратной функции в точке x = 1.
Решение. 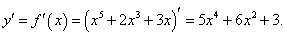 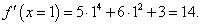 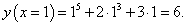 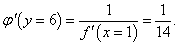 |
|
Пример 11
|
|
y = x2 − x.
Решение.
Найдем производную исходной функции
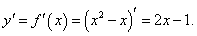 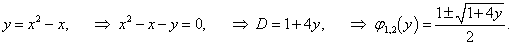 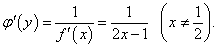 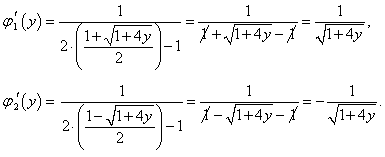 |
|
Пример 12
|
|
Дана функция e x + 2x + 1. Найти производную обратной функции при x = 0.
Решение. 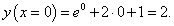 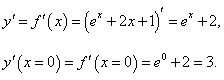 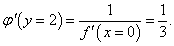 |
|
Пример 13
|
|
Для функции y = sin (x − 1) + x2 найти производную обратной функции в точке x = 1.
Решение. 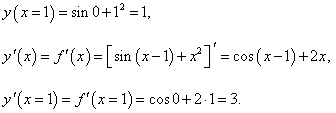 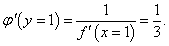 |
|
Пример 14
|
|
Найти производную обратной функции для y = x2 + 2ln x и вычислить ее значение в точке x = 1.
Решение. 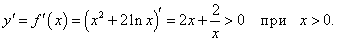 По теореме о производной обратной функции имеем 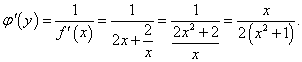 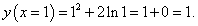 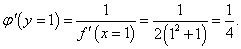 |
|
Пример 15
|
|
Найти производную обратной функции для y = x3 − 3x и вычислить ее значение при x = −2.
Решение. 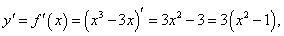
1) x ∈ (−∞, −1) − функция возрастает;
2) x ∈ (−1, 1) − функция убывает;
3) x ∈ (1, ∞) − функция возрастает.
Каждому интервалу можно сопоставить свою обратную функцию. Далее мы считаем, что рассматривается обратная функция, соответствующая первому интервалу, который содержит точку x = −2.Производная обратной функции имеет вид: 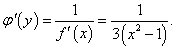 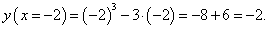 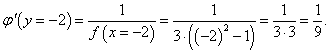 |
|
Пример 16
|
|
Найти производную обратной функции для y = 2x3 − 1 и вычислить ее значение при x = 2.
Решение. 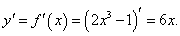 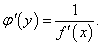 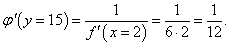 |
|
Пример 17
|
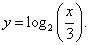
Решение.
Функция y = f (x) = log3(x/3) определена при x > 0 и монотонно возрастает на этом интервале. Следовательно, она имеет обратную функцию 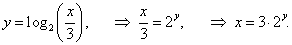 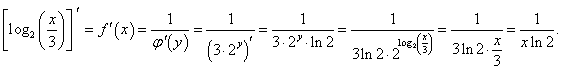 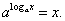 |
|
Пример 18
|
|
Найти значение производной арксеканса y = arcsec x при x = √2.
Решение.  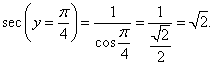 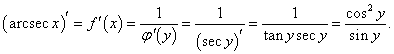 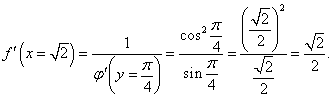 |
|
Пример 19
|
|
Найти производную функции обратной к функции y = x ⋅ 3 x при условии x > 0.
Решение. 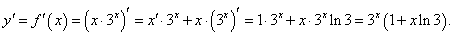 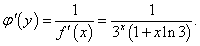 |
|
Пример 20
|
|
Найти производную функции y = Arsh x (обратный гиперболический синус).
Решение. 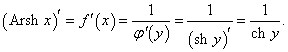 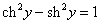 Отсюда находим 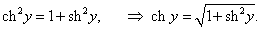 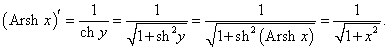 |