|
Тригонометрические пределы
|
|
Основной тригонометрический предел (первый замечательный предел) имеет вид
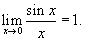 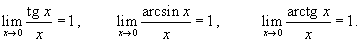 |
|
Пример 1
|
|
Вычислить предел
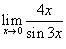 . .
Решение. 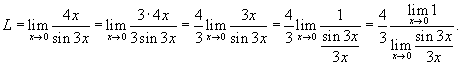  , то , то
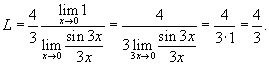 |
|
Пример 2
|
|
Вычислить предел
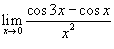 . .
Решение. 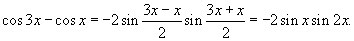 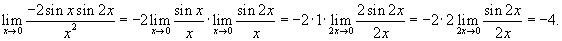 |
|
Пример 3
|
|
Вычислить предел
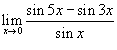 . .
Решение. 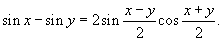 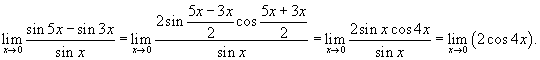 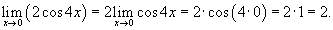 |
|
Пример 4
|
|
Вычислить предел
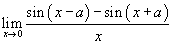 . .
Решение. 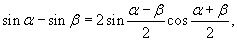 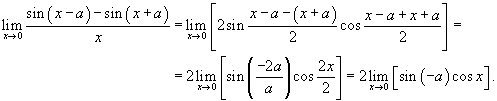 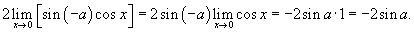 |
|
Пример 5
|
|
Вычислить предел
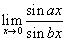 . .
Решение. 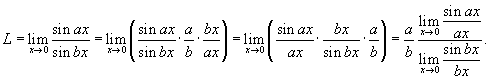 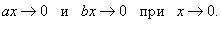 Тогда Тогда
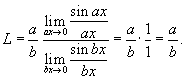 |
|
Пример 6
|
|
Найти предел
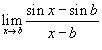 . .
Решение. 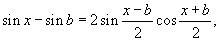 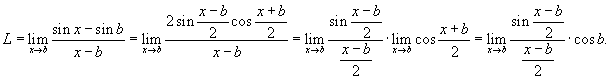 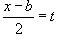 . Если . Если 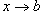 , то , то 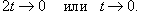 Тогда Тогда
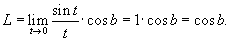 |
|
Пример 7
|
|
Найти предел
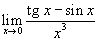 . .
Решение. 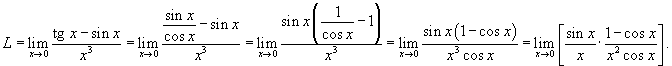 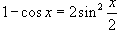 , то предел равен , то предел равен
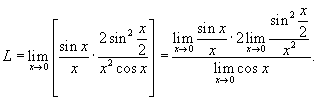 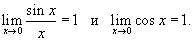 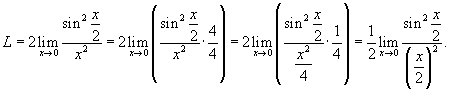 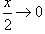 при при 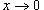 , получаем окончательный ответ , получаем окончательный ответ
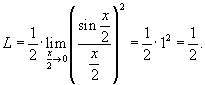 |
|
Пример 8
|
|
Найти предел
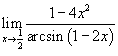 . .
Решение. 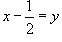 . Если . Если 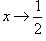 , то , то 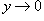 . Тогда . Тогда
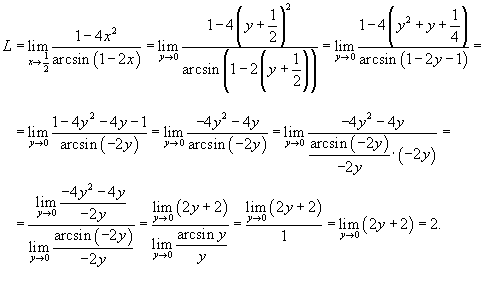 |
|
Пример 9
|
|
Найти предел
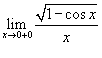 . .
Решение. 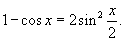 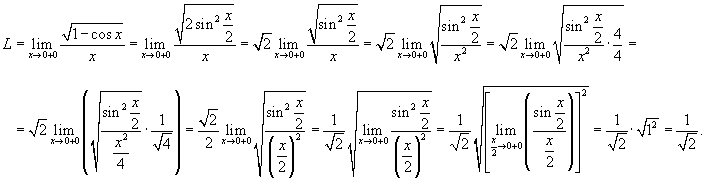 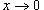 на на 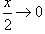 . . |
|
Пример 10
|
|
Найти предел
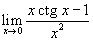 . .
Решение. 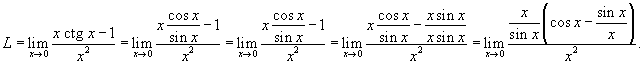 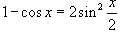 , получаем , получаем
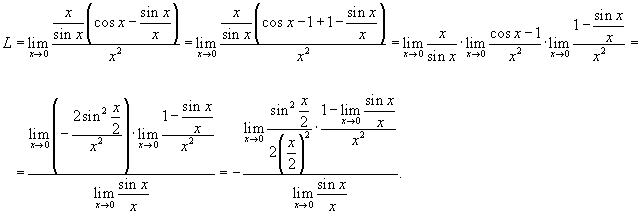 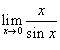 равен 1 и равен 1 и 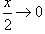 при при 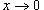 . В результате получаем ответ . В результате получаем ответ
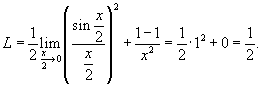 |