|
|
|
|
Свойства несобственного интеграла
|
|
|
Подынтегральные функции: f, g
Аргумент (независимая переменная): x
|
Пределы интегрирования: a, b, c, n
Малые действительные числа: τ, ε
|
-
Определенный интеграл 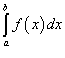 называется несобственным интегралом, называется несобственным интегралом,
• если нижний предел интегрирования a или верхний предел b (или оба предела) являются бесконечными,
• или если функция f(x) имеет точки разрыва в интервале [a, b].
Таким образом, несобственный интеграл − это интеграл по неограниченному множеству или от неограниченной функции.
-
Если f(x) − непрерывная функция на интервале [a, ∞), то несобственный интеграл выражается через предел в виде
-
Если f(x) − непрерывная функция на интервале [−∞, b), то несобственный интеграл определяется формулой
Примечание: несобственные интегралы в формулах 2,3 являются сходящимися, если верхний или нижний предел существуют и конечны. В противном случае несобственные интегралы являются расходящимися.
-
Несобственный интеграл с бесконечным нижним и верхним пределом.
Если для некоторого действительного числа c оба интеграла в правой части сходятся, то несобственный интеграл 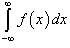 также сходится. В противном случаем он расходится. также сходится. В противном случаем он расходится.
-
Теоремы сравнения
Пусть f(x) и g(x) − непрерывные функции на интервале [a, ∞). Предположим, что 0 ≤ g(x) ≤ f(x) для всех x на интервале [a, ∞). Тогда справедливы следующие теоремы сравнения для несобственных интегралов от функций f(x) и g(x):
• Если 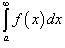 сходится, то сходится, то 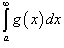 также сходится. также сходится.
• Если 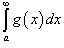 расходится, то расходится, то 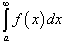 также расходится. также расходится.
-
Абсолютная сходимость
Если 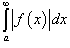 сходится, то несобственный интеграл сходится, то несобственный интеграл 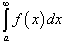 является абсолютно сходящимся. является абсолютно сходящимся.
-
Интеграл от разрывной функции (точка разрыва на границе интервала)
Пусть функция f(x) является непрерывной всюду на интервале [a, b), а в точке x = b терпит разрыв. Тогда справедлива следующая предельная формула:
-
Интеграл от разрывной функции (точка разрыва внутри интервала)
Пусть f(x) является непрерывной функцией для всех действительных чисел x в замкнутом интервале [a, b], исключая некоторую внутреннюю точку c ∈ (a, b). Тогда
|
|
|
|