Тройной интеграл от функции f(x, y, z) в параллелепипеде [a, b]×[c, d]×[r, s] определяется как предел интегральной суммы (суммы Римана)

где (u_i , v_j, w_k) − некоторая точка в параллелепипеде (x_i−1, x_i)×(y_i−1, y_i)×(z_i−1, z_i),
а соответствующие приращения переменных равны Δx_i = x_i − x_i−1, Δy_i = y_i − y_i−1, Δz_i = z_i − z_i−1.

Тройной интеграл от суммы функций равен сумме интегралов от этих функций:

Тройной интеграл от разности функций равен разности интегралов от соответствующих функций:

Постоянный множитель можно выносить за знак тройного интеграла:

Если f(x, y, z) ≥ 0, а G и T являются непересекающимися областями, то

Здесь G ∪ T обозначает объединение областей интегрирования G и T.

Выражение тройного интеграла через двойной интеграл
Если область интегрирования G состоит из множества точек (x, y, z), удовлетворяющих условию
(x, y) ∈ R,   λ₁(x, y) ≤ z ≤ λ₂(x, y),
то тройной интеграл выражается в виде

где R − проекция области G на плоскость Oxy.

Выражение тройного интеграла через повторный интеграл
Если область интегрирования G состоит из множества точек (x, y, z), таких что
a ≤ x ≤ b ,   φ₁(x) ≤ y ≤ φ₂(x) ,   λ₁(x, y) ≤ z ≤ λ₂(x, y),
то тройной интеграл равен

Тройной интеграл в параллелепипеде
Если G является параллелепипедом [a, b]×[c, d]×[r, s], то

В частном случае, когда подынтегральная функция f(x,y,z) представляет собой произведение g(x)h(y)k(z), тройной интеграл записывается в виде

Замена переменных

где 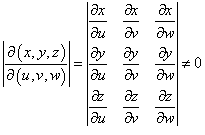− якобиан преобразования (x, y, z) → (u, v, w), а S является образом области интегрирования G и вычисляется подстановкой x = x(u, v, w), y = y(u, v, w), z = z(u, v, w) в определение G.

Тройной интеграл в цилиндрических координатах
Дифференциал dxdydz в цилиндрических координатах определяется выражением

Пусть область интегрирования G задана неравенствами
(x, y) ∈ R,   λ₁(x, y) ≤ z ≤ λ₂(x, y),
где R является проекцией области G на плоскость Oxy. Тогда

Здесь S представляет собой образ области G в цилиндрических координатах.

Тройной интеграл в сферических координатах
Дифференциал dxdydz в сферических координатах выражается формулой

В сферических координатах тройной интеграл записывается как

где S является образом области G в сферических координатах. Угол θ изменяется от 0 до 2π, а угол φ − в пределах от 0 до π.

Объем тела

Объем тела в цилиндрических координатах

Объем тела в сферических координатах

Масса тела

где тело занимает область G, а его плотность в точке (x, y, z) равна μ(x, y, z).

Координаты центра масс тела

− первые моменты относительно координатных плоскостей x = 0, y = 0 и z = 0, а функция μ(x, y, z) описывает плотность тела.

Моменты инерции тела относительно координатных плоскостей Oxy (или z = 0), Oyz (x = 0) Oxz (y = 0).

Моменты инерции тела относительно координатных осей Ox, Oy, Oz.

Полярный момент инерции