Поверхностный интеграл первого рода
Пусть поверхность S задана вектором
r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k,
где (u, v) принимает значения из некоторой области определения D(u, v) в плоскости Ouv. Поверхностный интеграл первого рода от скалярной функции f(x, y, z) по поверхности S определяется в виде

где частные производные ∂r/∂u и ∂r/∂v выражаются формулами

а 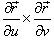представляет собой векторное произведение.

Если поверхность S задана явным уравнением z = z(x, y), где z(x, y) − дифференцируемая функция в области D(x, y), то поверхностный интеграл (первого рода) записывается как

Поверхностный интеграл второго рода от векторного поля F по поверхности S
     •  Если поверхность S ориентирована внешней нормалью, то

     •  Если поверхность S ориентирована внутренней нормалью, то

Здесь величина dS = ndS называется векторным элементом поверхности. Точка в подынтегральном выражении означает скалярное произведение соответствующих векторов. Частные производные ∂r/∂u и ∂r/∂v определяются формулами

Если поверхность S задана явным уравнением z = z(x, y), где z(x, y) является дифференцируемой функцией в области D(x, y), то поверхностный интеграл (второго рода) записывается следующим образом:
     •  Если поверхность S ориентирована внешней нормалью
        (k-компонент вектора нормали является положительным), то

     •  Если поверхность S ориентирована внутренней нормалью
        (k-компонент вектора нормали является отрицательным), то

Поверхностный интеграл второго рода в координатной форме

где P(x, y, z), Q(x, y, z), R(x, y, z) − компоненты векторного поля F, а cos α, cos β, cos γ − направляющие косинусы внешней нормали n к поверхности S.

Поверхностный интеграл второго рода в параметрической форме
Если поверхность S задана в параметрической форме вектором r(x(u, v), y(u, v), z(u, v)), то поверхностный интеграл записывается в виде

где (u, v) принимает значения в области D(u, v) в плоскости Ouv.

Теорема Остроградского-Гаусса

где F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z) − векторное поле, компоненты P, Q, R которого имеют непрерывные частные производные, а через

обозначена дивергенция поля F. Символ 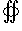указывает, что поверхностный интеграл вычисляется по замкнутой поверхности.

Формула Остроградского-Гаусса в координатной форме

Теорема Стокса

где F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z) является векторным полем, компоненты P, Q, R которого имеют непрерывные частные производные, а через

обозначен ротор векторного поля F. Символ 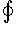в левой части формулы Стокса указывает, что криволинейный интеграл вычисляется по замкнутому контуру.

Формула Стокса в координатной форме

Площадь поверхности

Если поверхность S задана в параметрической форме вектором r(u, v) = x(u, v)i + y(u, v)j + z(u, v)k, то площадь поверхности выражается формулой

где D(u, v) является областью, в которой задана поверхность r(u, v).

Если поверхность S задана в явном виде функцией z(x, y), то площадь поверхности равна

где D(u, v) является проекцией поверхности S на плоскость Oxy.

Масса поверхности

где μ(x, y, z) − масса на единицу площади (функция плотности).

Координаты центра масс поверхности

− первые моменты поверхности относительно координатных плоскостей x = 0, y = 0, z = 0, соответственно, μ(x, y, z) − функция плотности.

Моменты инерции поверхности относительно координатных плоскостей
Моменты инерции относительно плоскостей Oxy (или z = 0), Oyz (x = 0), Oxz (y = 0) выражаются, соответственно, формулами

Моменты инерции поверхности относительно координатных осей
Моменты инерции поверхности относительно осей Ox, Oy, Oz вычисляются по формулам

Объем тела, ограниченного замкнутой поверхностью

Сила притяжения между поверхностью и точечным телом

где m − масса точечного тела, μ(x, y, z) − функция плотности, G − гравитационная постоянная, r = (x − x₀, y − y₀, z − z₀).

Сила давления

где давление p(r) действует на поверхность S, заданную позиционным вектором r.

Поток жидкости через поверхность S

где v(r) − скорость жидкости.

Поток вещества через поверхность S

где F = ρv − векторное поле, ρ − плотность вещества.

Заряд поверхности

где σ(x, y) − поверхностная плотность заряда.

Теорема Гаусса
Поток электрического поля через любую замкнутую поверхность пропорционален величине заряда, ограниченного данной поверхностью:

где E − напряженность электрического поля, Φ − поток электрического поля, ε₀ = 8,85 × 10⁻¹² Ф/м − диэлектрическая проницаемость вакуума.