Двойной интеграл от функции f(x, y) в прямоугольной области [a, b]×[c, d] определяется как предел интегральной суммы (суммы Римана)

где (u_i , v_j) обозначает некоторую точку в прямоугольнике (x_i−1, x_i)×(y_i−1, y_i)
и Δx_i = x_i − x_i−1, Δy_i = y_i − y_i−1.

Двойной интеграл от функции f(x, y) в произвольной области R определяется как

где прямоугольник [a, b]×[c, d] содержит область R, функция g(x, y) = f(x, y) если f(x, y) находится в R, и g(x, y) = 0 в противном случае.

Двойной интеграл от суммы функций равен сумме интегралов от этих функций:

Двойной интеграл от разности функций равен разности интегралов от этих функций:

Постоянный коэффициент можно выносить за знак двойного интеграла:

Если f(x, y) ≤ g(x, y) в области R, то справедливо неравенство

Если f(x, y) ≥ 0 в области R и S ⊂ R, то

Если f(x, y) ≥ 0 в области R, а R и S − непересекающиеся области, то

Здесь R ∪ S является объединением областей интегрирования R и S.

Повторный интеграл в области типа I

где область интегрирования R определяется неравенствами
R = {(x,y)| a ≤ x ≤ b, p(x) ≤ y ≤ q(x)}.

Повторный интеграл в области типа II

где область интегрирования R определяется неравенствами
R = {(x,y)| u(y) ≤ x ≤ v(y), c ≤ y ≤ d}.

Двойной интеграл в прямоугольной области
Если R является прямоугольной областью [a, b]×[c, d], то

В частном случае, когда подынтегральная функция f(x, y) представляет собой произведение g(x)h(y), двойной интеграл можно записать в виде

Замена переменных

где 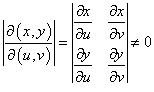− якобиан преобразования (x, y) → (u, v), а S является образом области R и вычисляется подстановкой x = x(u, v), y = y(u, v) в определение R.

Полярные координаты
x = r cos θ, y = r sin θ

Двойной интеграл в полярных координатах
Дифференциал dxdy в полярных координатах определяется выражением

Пусть область интегрирования R определяется соотношениями
0 ≤ g(θ) ≤ r ≤ h(θ), α ≤ θ ≤ β, где β − α ≤ 2π. Тогда

Двойной интеграл в полярном прямоугольнике
Если область интегрирования R представляет собой полярный прямоугольник, заданный неравенствами 0 ≤ a ≤ r ≤ b, α ≤ θ ≤ β, где β − α ≤ 2π, то двойной интеграл равен

Площадь области типа I

Площадь области типа II

Объем тела

Если R является областью типа I, ограниченная линиями x = a, x = b, y = h(x), y = g(x), то

Если R является областью типа II и ограничена линиями y = c, y = d, x = q(y), x = p(y), то

Объем тела между двумя поверхностями
Если  f (x, y) ≥ g (x, y) в области R, то объем тела между поверхностями z₁(x, y) и z₂(x, y) в данной области равен

Площадь и объем в полярных координатах
Пусть область S задана в полярных координатах в плоскости Oxy и ограничена линиями θ = α, θ = β, r = h(θ), r = g(θ). Пусть также в области S задана функция f(r, θ). Тогда площадь области S и объем тела, ограниченного поверхностью f(r, θ), определяются формулами

Площадь поверхности

Масса пластины

где пластина расположена в области R и ее плотность в точке (x, y) равна ρ(x, y).

Статические моменты пластины
Момент пластины относительно оси Ox определяется формулой

Аналогично, момент пластины относительно оси Oy выражается в виде

Моменты инерции пластины
Момент инерции пластины относительно оси Ox вычисляется по формуле

Момент инерции пластины относительно оси Oy равен

Полярный момент инерции определяется выражением

Координаты центра масс пластины

Заряд пластины

где электрический заряд распределен по области R и его плотность в точке (x, y) равна σ(x, y).

Среднее значение функции