Ряд Тейлора
Если функция f(x) имеет непрерывные производные до (n + 1)-го порядка включительно, то ее можно разложить в степенной ряд в точке x = a по формуле Тейлора:

где остаточный член R_n в форме Лагранжа определяется выражением

Если данное разложение сходится в некотором интервале x с центром в точке a, т.е. 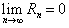, то оно называется рядом Тейлора, представляющим разложение функции f(x) в окрестности точки a.

Ряд Маклорена является частным случаем ряда Тейлора, когда разложение в степенной ряд производится в точке a = 0:

Ниже приводятся разложения некоторых функций в ряд Маклорена.