|
Теорема Остроградского-Гаусса
|
||||||
|
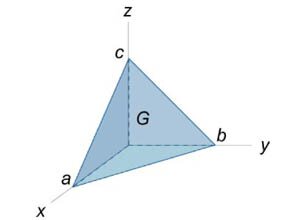
Обозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностью S с внешней нормалью. Предположим, что задано векторное поле
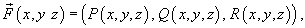 Согласно формуле Остроградского-Гаусса, 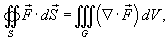 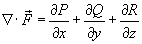 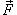 (она обозначается также символом (она обозначается также символом 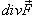 ). Символ ). Символ 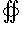 указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. указывает, что поверхностный интеграл вычисляется по замкнутой поверхности.Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме: 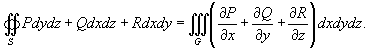 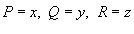 , получаем формулу для вычисления объема тела G: , получаем формулу для вычисления объема тела G:
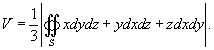 |
||||||
|
Пример 1
|
||||||
|
Вычислить поверхностный интеграл
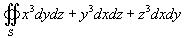 , где S − внешне ориентированная поверхность сферы, заданная уравнением , где S − внешне ориентированная поверхность сферы, заданная уравнением 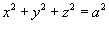 . .
Решение. 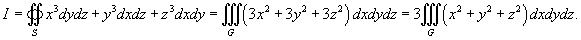 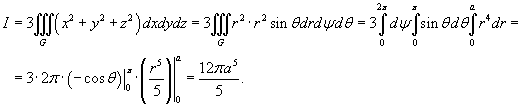 |
||||||
|
Пример 2
|
||||||
|
Применяя теорему Остроградского-Гаусса, вычислить поверхностный интеграл
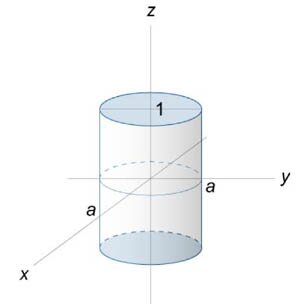
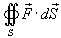 от векторного поля от векторного поля 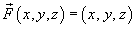 , где S − поверхность тела, образованного цилиндром , где S − поверхность тела, образованного цилиндром 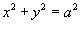 и плоскостями и плоскостями Решение. 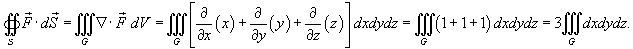 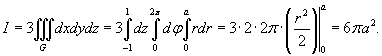
|
||||||
|
Пример 3
|
||||||
|
Используя формулу Остроградского-Гаусса, оценить поверхностный интеграл
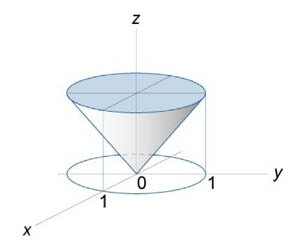
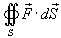 от векторного поля от векторного поля 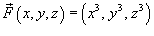 , где S − поверхность тела, ограниченного , где S − поверхность тела, ограниченного 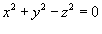 и плоскостью и плоскостью Решение. 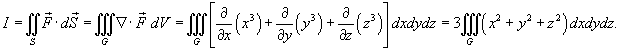 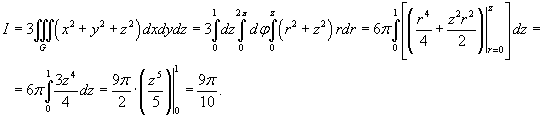 |
||||||
|
Пример 4
|
||||||
|
Вычислить поверхностный интеграл
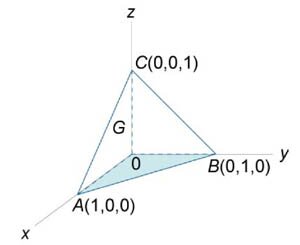
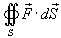 от векторного поля от векторного поля 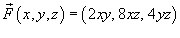 , где S является поверхностью тетраэдра с вершинами , где S является поверхностью тетраэдра с вершинами Решение. 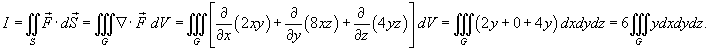 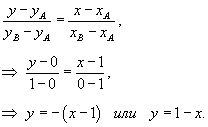 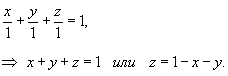 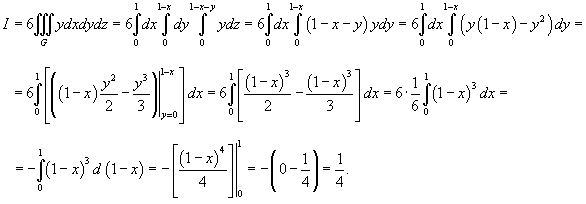
|
||||||
|
Пример 5
|
||||||
|
Вычислить поверхностный интеграл
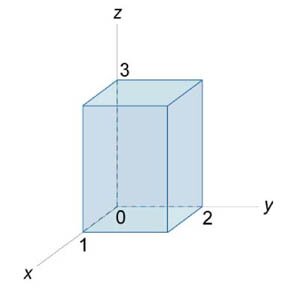
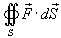 от векторного поля от векторного поля 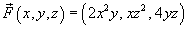 , где S − поверхность параллелепипеда, образованного плоскостями , где S − поверхность параллелепипеда, образованного плоскостями Решение. 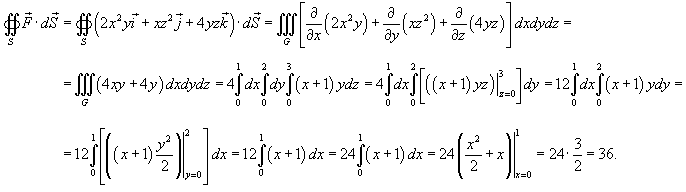 |
||||||
|
Пример 6
|
||||||
|
Найти интеграл
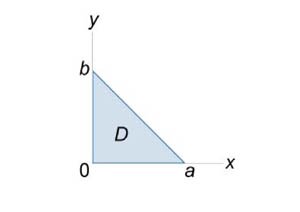
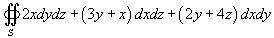 , где S − внешняя поверхность пирамиды , где S − внешняя поверхность пирамиды 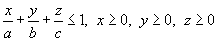 (рисунок 5). (рисунок 5).
Решение.
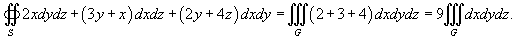 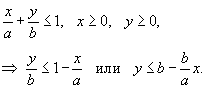 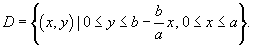 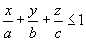 относительно переменной z, получаем относительно переменной z, получаем
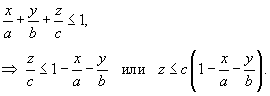 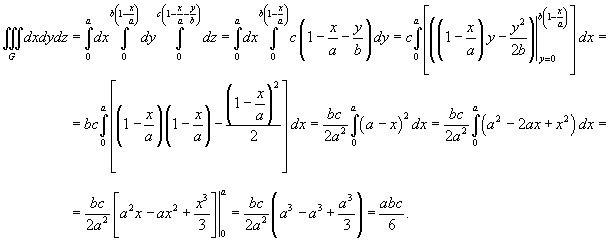 |
||||||