|
Логарифмическое дифференцирование
|
|
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.
Рассмотрим этот подход более детально. Пусть дана функция 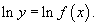 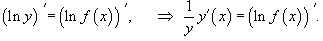 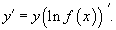 Данный метод позволяет также эффективно вычислять производные показательно-степенных функций, то есть функций вида 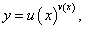 В приведенных ниже примерах вычислить производную функции y(x), используя логарифмическое дифференцирование. |
|
Пример 1
|
|
y = x x, x > 0.
Решение.
Сначала прологарифмируем левую и правую части уравнения:
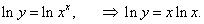 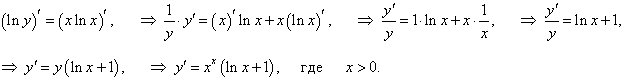 |
|
Пример 2
|
|
y = x ln x, x > 0.
Решение.
Применяем логарифмическое дифференцирование:
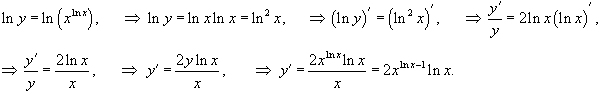 |
|
Пример 3
|
|
y = x cos x, x > 0.
Решение.
Логарифмируем заданную функцию:
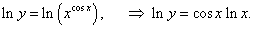 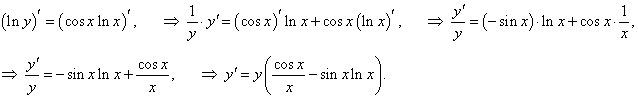 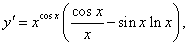 |
|
Пример 4
|
|
y = x 2x, (x > 0, x ≠ 1).
Решение.
Логарифмируя обе части, записываем следующее равенство:
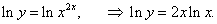 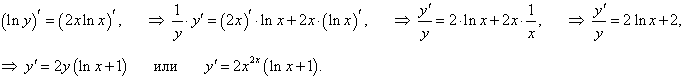 |
|
Пример 5
|
|
y = (x − 1)2 (x − 3)5.
Решение.
Прологарифмируем сначала обе части:
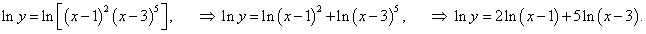 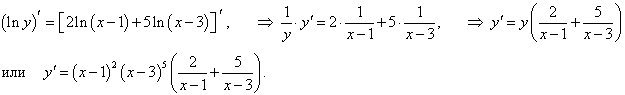 |
|
Пример 6
|
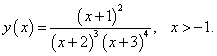
Решение.
Возьмем логарифм от обеих частей:
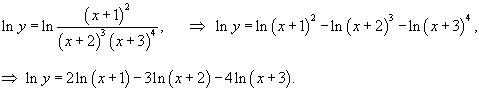 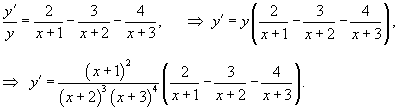 |
|
Пример 7
|
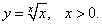
Решение.
Прологарифмируем данное равенство:
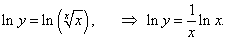 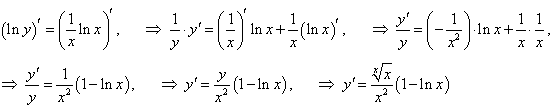 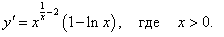 |
|
Пример 8
|
|
y = (ln x) x, x > 1.
Решение.
Следуя общей схеме, имеем:
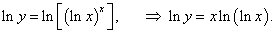 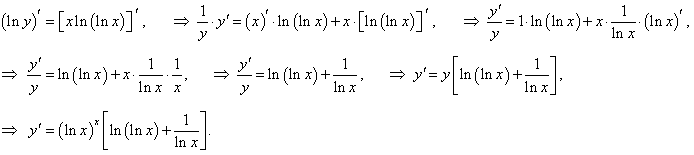 |
|
Пример 9
|
|
y = x x 2, (x > 0, x ≠ 1).
Решение.
Предварительно логарифмируя обе части, получаем:
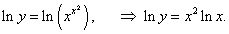 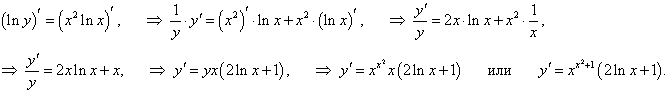 |
|
Пример 10
|
|
y = x x n, (x > 0, x ≠ 1).
Решение.
Логарифмируем обе части:
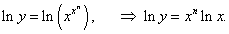 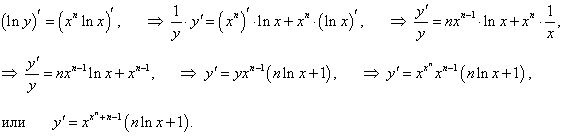 |
|
Пример 11
|
|
y = x 2 x, (x > 0, x ≠ 1).
Решение.
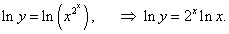 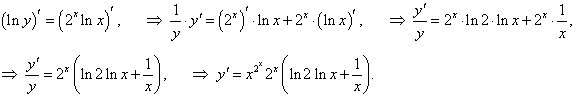 |
|
Пример 12
|
|
y = 2 x x, (x > 0, x ≠ 1).
Решение.
Дифференцируя как сложную функцию, находим:
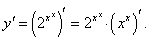 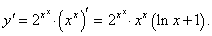
|
|
Пример 13
|
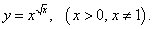
Решение.
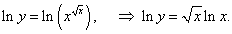 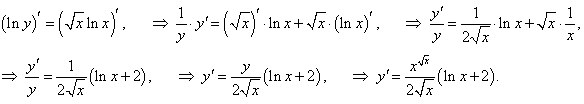 |
|
Пример 14
|
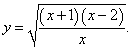
Решение.
Будем рассматривать данную функцию при x > 2. Тогда логарифмируя левую и правую части равенства, имеем:
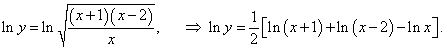 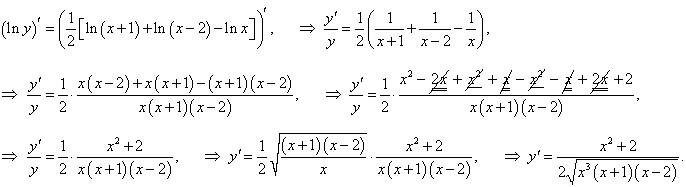 |
|
Пример 15
|
|
y = x x x, (x > 0, x ≠ 1).
Решение.
Логарифмируем заданную функцию:
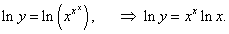 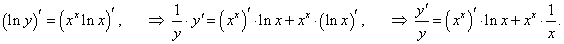 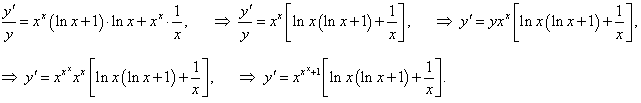
|
|
Пример 16
|
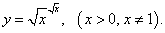
Решение.
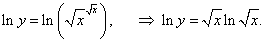 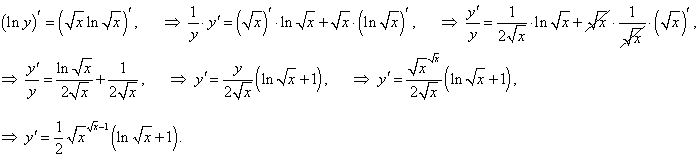 |
|
Пример 17
|
|
y = sin x cos x.
Решение.
В данном примере предполагается, что переменная x удовлетворяет области определения, имеющей вид:
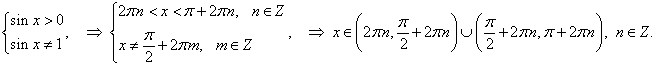 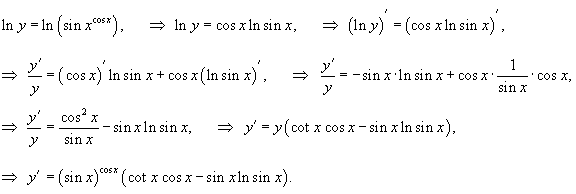 |
|
Пример 18
|
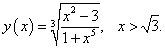
Решение.
Сначала возьмем логарифм от обеих частей:
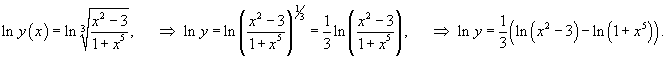 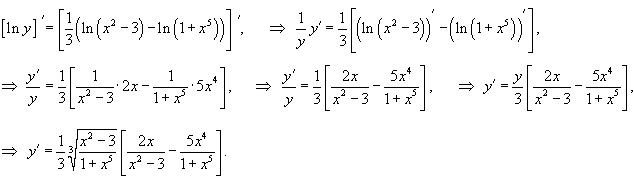 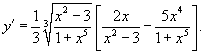 |
|
Пример 19
|
|
y = (cos x) arcsin x.
Решение.
Логарифмируем обе части равенства:
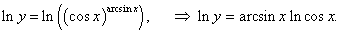
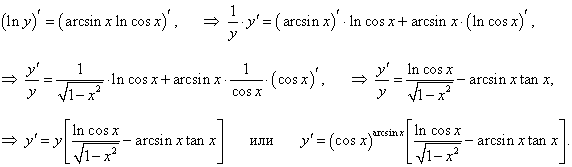
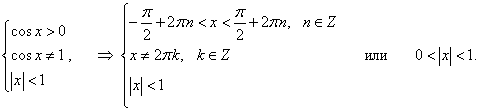
|
|
Пример 20
|
|
y = (sin x) arctan x.
Решение.
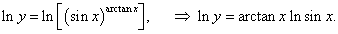
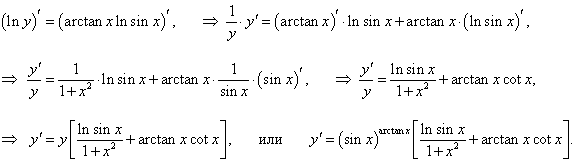
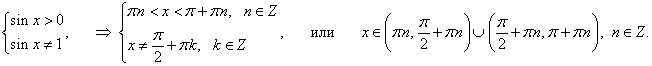
|