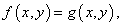|
Производная неявной функции
|
|
Если функция описывается уравнением y = f(x), где переменная y находится в левой части, а правая часть зависит только от аргумента x, то говорят, что функция задана в явном виде. Например, следующие функции заданы явно:
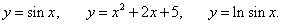 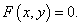 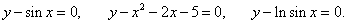 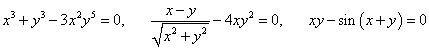 Хорошая новость состоит в том, что для нахождения производной y'(x) неявно заданной функции нет необходимости преобразовывать ее в явную форму. Для этого, зная уравнение F(x, y) = 0, достаточно выполнить следующие действия:
|
|
Пример 1
|
|
Найти производную функции, заданной уравнением
Решение. 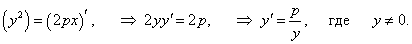 |
|
Пример 2
|
|
Продифференцировать функцию
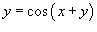 . .
Решение. 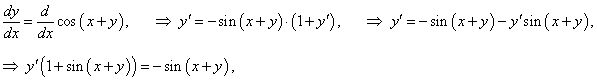 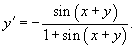 |
|
Пример 3
|
|
Найти уравнение касательной к кривой
Решение. 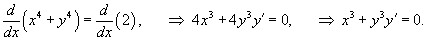 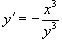 . В точке . В точке 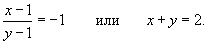 |
|
Пример 4
|
|
Вычислить производную функции
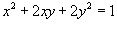 при условии при условии Решение. 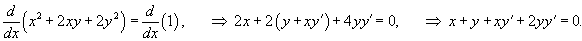 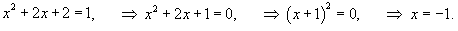 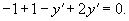 |
|
Пример 5
|
|
Дано уравнение окружности
Найти производную Решение. 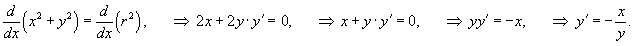 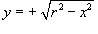 . Отсюда находим, что производная равна . Отсюда находим, что производная равна
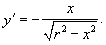 |
|
Пример 6
|
|
Вычислить производную функции, заданной уравнением
Решение. 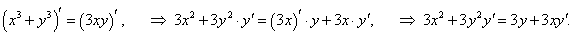 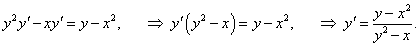 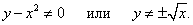 |
|
Пример 7
|
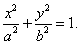
Решение.
Записанное уравнение представляет собой уравнение эллипса. Дифференцируя обе части и учитывая, что y − функция от x, получаем:
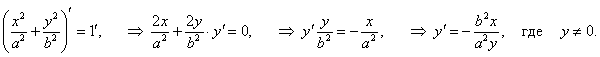 |
|
Пример 8
|
|
Решение.
Дифференцируем обе части и решаем полученное уравнение относительно y' :
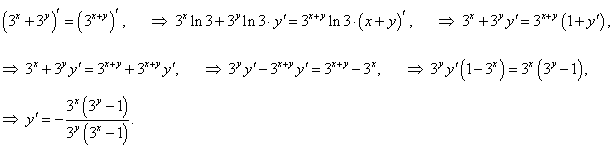 |
|
Пример 9
|
|
Найти производную астроиды x2/3 + y2/3 = a2/3.
Решение. 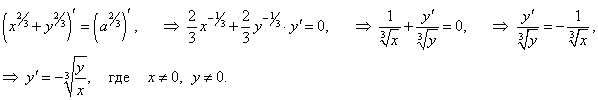 |
|
Пример 10
|
|
Найти производную y'(x) функции, описывающей общее уравнение кривой второго порядка:
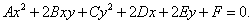
Решение.
Дифференцируем данное уравнение по x, принимая во внимание, что y − это функция от x:
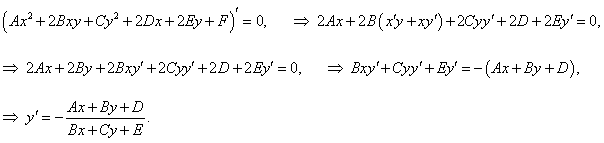 |
|
Пример 11
|
|
Найти значение производной y'(x) в точке x = 0 для функции, заданной уравнением ey + xy = e.
Решение. 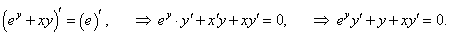 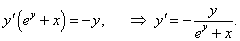 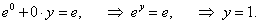 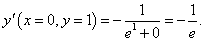 |
|
Пример 12
|
|
Решение.
Как обычно, дифференцируем обе части по x:
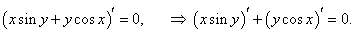 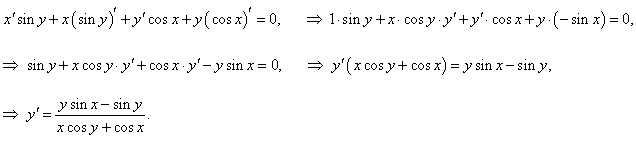 |
|
Пример 13
|
|
Решение.
Дифференцируем обе части уравнения по x:
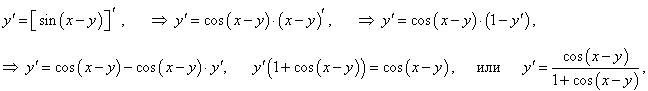 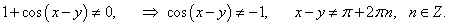 |
|
Пример 14
|
|
Решение.
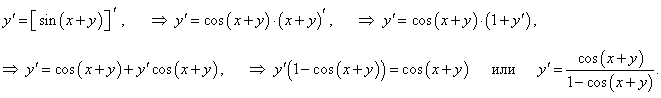 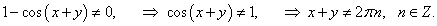 |
|
Пример 15
|
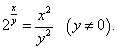
Решение.
Следуя описанной схеме, имеем:
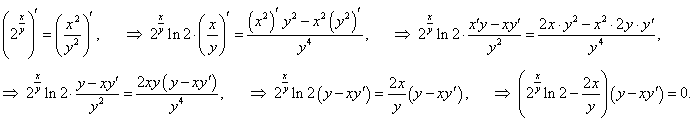 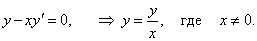 |
|
Пример 16
|
|
Решение.
Вычисляем производную y'(x) по общей схеме, рассмотренной выше. В результате получаем:
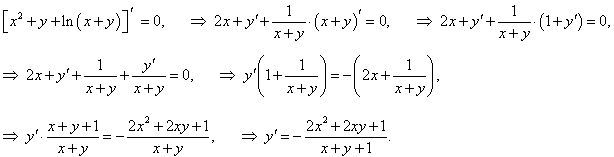 |
|
Пример 17
|
|
Найти производную в точке x = 2 функции, заданной уравнением
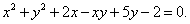
Решение.
Предварительно вычислим значение функции y в точке x = 2:
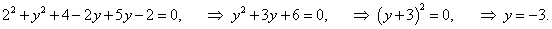 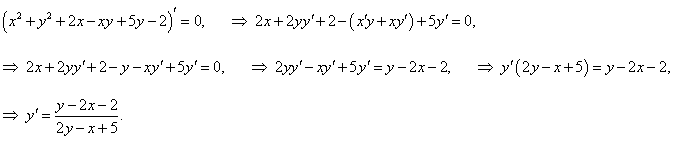 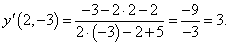 |
|
Пример 18
|
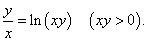
Решение.
Используя правила дифференцирования произведения функций, частного функций и сложной функции, получаем:
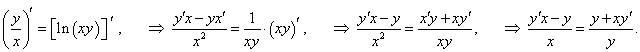 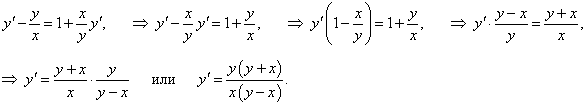 |
|
Пример 19
|
|
Найти производную функции, заданной уравнением x + y = arctan (xy).
Решение. 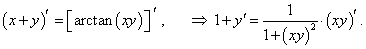 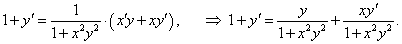 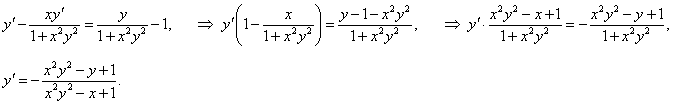 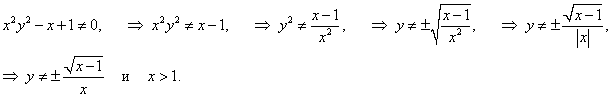 |
|
Пример 20
|
|
Решение.
Предварительно прологарифмируем обе части уравнения:
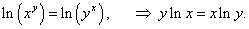 Дифференцируя обе части равенства по x и учитывая, что y − функция от x, получаем: 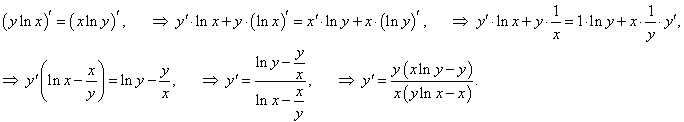  |