|
Дифференциальные операторы
|
|
Примеры дифференциальных операторов
Дифференциальные операторы представляют собой обобщение операции дифференцирования. Простейший дифференциальный оператор D, действуя на функцию y, "возвращает" первую производную этой функции:
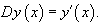 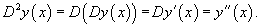 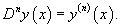 Дифференциальные операторы могут иметь и более сложный вид − в зависимости от образующих их дифференциальных выражений. Так например, в векторном анализе часто встречается дифференциальный оператор набла, определяемый как 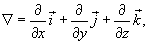 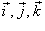 − единичные векторы вдоль координатных осей 0x, 0y, 0z. − единичные векторы вдоль координатных осей 0x, 0y, 0z.В результате действия оператора ∇ на скалярное поле F, мы получаем градиент поля F: 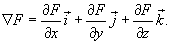 Скалярное произведение вектора ∇ и векторного поля 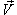 известно как дивергенция вектора известно как дивергенция вектора  : :
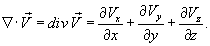 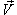 мы получаем ротор вектора мы получаем ротор вектора 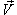 : :
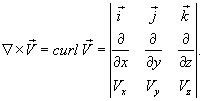 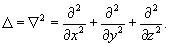  и используется в теории относительности, электромагнетизме и других областях физики. В четырехмерном пространстве-времени и используется в теории относительности, электромагнетизме и других областях физики. В четырехмерном пространстве-времени 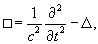 Введение дифференциальных операторов позволяет исследовать дифференциальные уравнения в терминах теории операторов и функционального анализа. Такой обобщенный подход оказывается мощным и эффективным. В частности, в приложении к линейным дифференциальным уравнением n-го порядка мы получаем компактный способ записи уравнений, а в некоторых случаях − возможность их быстрого решения.
Дифференциальный оператор L(D)
Рассмотрим линейное дифференциальное уравнение n-го порядка:
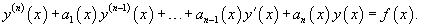 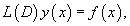 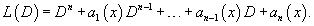 Рассмотрим некоторые свойства введенного оператора 1) Оператор 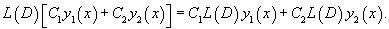 2) Коммутативный закон сложения: 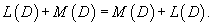 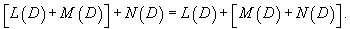 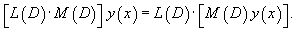 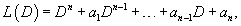 Для таких операторов выполняются свойства 4-6: 4) Коммутативный закон умножения: 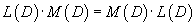 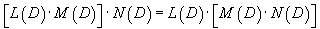 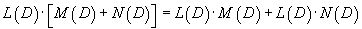 7) Как видно, дифференциальные операторы |
|
Пример 1
|
|
Проверить, выполняется ли коммутативный закон умножения для операторов
Решение. 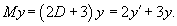 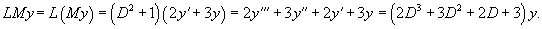 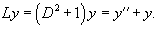 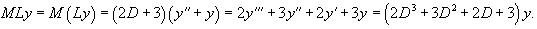 |
|
Пример 2
|
|
Проверить, выполняется ли коммутативный закон умножения для операторов
Решение. 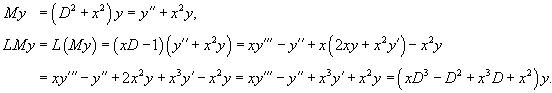 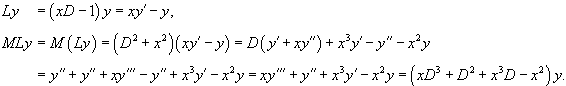 |
|
Пример 3
|
|
Найти частное решение дифференциального уравнения
Решение. 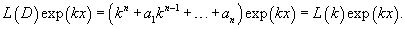 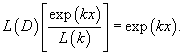 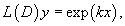 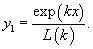 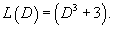 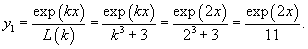 |
|
Пример 4
|
|
Найти частное решение дифференциального уравнения
Решение. 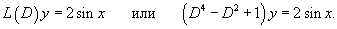 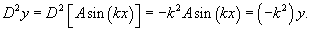 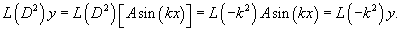 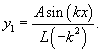 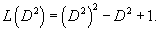 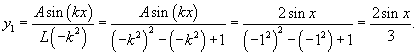 |