Экономические задачи на оптимизацию

Приведенные ниже задачи описывают разнообразные ситуации, с которыми корпорации и компании могут встретиться в своей экономической деятельности. В каждой из этих задач необходимо построить функцию, устанавливающую связь между двумя экономическими величинами (например, между объемом производства и прибылью компании), и исследовать ее на экстремальное значение. Задачи на оптимизацию такого типа эффективно решаются с использованием производной.

   Пример 1

Завод изготавливает и продает полупроводниковые приборы. Удельные расходы (в расчете на один прибор) зависят от объема производства и включают в себя постоянную часть в размере \(1000\) (руб/прибор) и переменную часть \(2n\) (руб/прибор), где \(n\) − число приборов, изготовленных за месяц. Цена прибора, в свою очередь, зависит от объема производства по закону \(p\left( n \right) = 10000 - n\) (руб/прибор). Определить, при каком объеме производства прибыль будет максимальной? Доход от продажи приборов, изготовленных в течение месяца, равен \[R\left( n \right) = np\left( n \right) = n\left( {10000 - n} \right).\] Месячные расходы при этом составляют \[C\left( n \right) = n\left( {1000 + 2n} \right).\] Тогда прибыль определяется формулой \[ {P\left( n \right) = R\left( n \right) - C\left( n \right) } = {n\left( {10000 - n} \right) - n\left( {1000 + 2n} \right) } = {10000n - {n^2} - 1000n - 2{n^2} } = {9000n - 3{n^2}.} \] Исследуем функцию прибыли на экстремум. При этом будем считать, что \(n\) является действительным числом. Дифференцируя по \(n,\) получаем: \[ {P'\left( n \right) = {\left( {9000n - 3{n^2}} \right)^\prime } = 9000 - 6n = 0,}\;\; {\Rightarrow n = \frac{{9000}}{6} = 1500.} \] Вычислим также вторую производную: \[P''\left( n \right) = {\left( {9000 - 6n} \right)^\prime } = - 6 < 0.\] Поскольку вторая производная всюду отрицательна, то решение \(n = 1500\) является точкой максимума, то есть при производстве \(1500\) приборов в месяц прибыль предприятия будет максимальной.

   Пример 2

На изготовление \(x\) единиц товара фирма затрачивает \[C\left( x \right) = a{x^2} + bx\;\;\text{рублей},\] где \(a\) и \(b\) − некоторые действительные числа. Товар продается по цене \(p\) рублей за штуку. Определить объем продаж, при котором прибыль будет наибольшей. При продаже \(x\) единиц товара фирма получает доход, равный \[R\left( x \right) = px.\] Следовательно, прибыль фирмы составляет \[ {P\left( x \right) = R\left( x \right) - C\left( x \right) } = {px - \left( {a{x^2} + bx} \right) } = {\left( {p - b} \right)x - a{x^2}.} \] Найдем производную функции \(P\left( x \right):\) \[ {P'\left( x \right) } = {{\left[ {\left( {p - b} \right)x - a{x^2}} \right]^\prime } } = {p - b - 2ax.} \] Производная равна нулю в точке \[ {P'\left( x \right) = 0,}\;\; {\Rightarrow p - b - 2ax = 0,}\;\; {\Rightarrow 2ax = p - b,}\;\; {\Rightarrow x = \frac{{p - b}}{{2a}}.} \] Рассмотрим вторую производную: \[P''\left( x \right) = {\left( {p - b - 2ax} \right)^\prime } = - 2a < 0.\] Так как вторая производная отрицательна, то точка \(x = \large\frac{{p - b}}{{2a}}\normalsize\) является точкой максимума, т.е. при данном объеме продаж прибыль фирмы будет наибольшей.

   Пример 3

Компания продает товар по цене \(100\) рублей, если объем партии не превышает \(5000\) единиц. При большем объеме предоставляется скидка в размере \(5\) рублей на каждую последующую тысячу, превышающую уровень \(5000.\) При каком объеме заказа компания получаем наибольший доход? Обозначим количество товара в партии через \(x.\) Если \(x \le 5000,\) то цена единицы товара по условию составляет \(100\) рублей. Если же \(x \gt 5000,\) то цена вычисляется по формуле \[ {p\left( x \right) } = {100 - 5 \cdot \frac{{x - 5000}}{{1000}} } = {100 - 0,005x + 25 } = {125 - 0,005x.} \] В первом случае, при \(x \le 5000,\) максимальный доход достигается при \(x = 5000.\) Он равен \[{R_1} = 5000 \cdot 100 = 500000\;\;\text{(руб)}.\] Во втором случае, при \(x \gt 5000,\) доход определяется следующей функцией: \[ {{R_2} = R\left( x \right) } = {xp\left( x \right) } = {x\left( {125 - 0,005x} \right) } = {125x - 0,005{x^2}\;\;\text{(руб)}.} \] Находим производную: \[ {R'\left( x \right) } = {{\left( {125x - 0,005{x^2}} \right)^\prime } } = {125 - 0,01x.} \] Приравнивая ее нулю, определяем критическую точку: \[ {R'\left( x \right) = 0,}\;\; {\Rightarrow 125 - 0,01x = 0,}\;\; {\Rightarrow x = \frac{{125}}{{0,01}} = 12500.} \] Заметим, что вторая производная функции \(R\left( x \right)\) всегда отрицательна: \[ {R''\left( x \right) } = {{\left( {125 - 0,01x} \right)^\prime } } = { - 0,01 < 0.} \] Поэтому найденная критическая точка соответствует максимуму функции \(R\left( x \right).\) Таким образом, доход компании будет максимальным при продаже партии товаров \(x = 12500\) единиц. Максимальный доход при этом составит \[ {{R_{\max }} } = {125 \cdot 12500 - 0,005 \cdot {12500^2} } = {781250\;\;\text{(руб)}.} \]

   Пример 4

В некотором государстве используется прогрессивная система налогообложения. Сумма налога состоит из линейной части, пропорциональной доходу, и нелинейной части, зависящей от дохода по степенному закону. Общая величина налога определяется формулой \[T\left( W \right) = aW + {\left( {bW + c} \right)^p},\] где \(W\) − доход, \(p\) − показатель степени, \(a, b, c\) − положительные коэффициенты. При каком уровне дохода ставка налога будет минимальной? Налоговая ставка \(r\) вычисляется по формуле \[ {r\left( W \right) = \frac{{T\left( W \right)}}{W} } = {\frac{{aW + {{\left( {bW + c} \right)}^p}}}{W} } = {a + \frac{{{{\left( {bW + c} \right)}^p}}}{W}.} \] Исследуем ее на экстремум. Находим производную: \[ {r'\left( W \right) = {\left[ {a + \frac{{{{\left( {bW + c} \right)}^p}}}{W}} \right]^\prime } } = {\frac{{p{{\left( {bW + c} \right)}^{p - 1}} \cdot W - {{\left( {bW + c} \right)}^p} \cdot 1}}{{{W^2}}} } = {\frac{{{{\left( {bW + c} \right)}^{p - 1}}\left[ {pW - \left( {bW + c} \right)} \right]}}{{{W^2}}} } = {\frac{{{{\left( {bW + c} \right)}^{p - 1}}\left[ {\left( {p - b} \right)W - c} \right]}}{{{W^2}}}.} \] Видно, что функция \(r\left( W \right)\) имеет три критических точки, но поскольку коэффициенты \(b, c > 0,\) то содержательное решение существует лишь в следующей точке: \[ {\left( {p - b} \right)W - c = 0,}\;\; {\Rightarrow W = \frac{c}{{p - b}}.} \] При переходе через это значение производная меняет знак с минуса на плюс, Следовательно, здесь функция \(r\left( W \right)\) достигает минимума, т.е. налоговая ставка при этом уровне дохода будет наименьшей.

   Пример 5

Компания изготавливает и продает \(1000\) изделий в месяц по цене \(2000\) рублей за штуку. При уменьшении цены на \(50\) рублей можно дополнительно продать еще \(50\) изделий в месяц. При какой цене фирма получит максимальный доход и каково его значение? Обозначим через \(x\) количество вычетов по \(50\) рублей из базовой цены \(2000\) рублей. Тогда цена одного изделия (при продаже более \(1000\) изделий в месяц) равна \(2000 - 50x.\) Общее количество проданных изделий будет составлять \(1000 + 50x\) штук. Полный доход описывается выражением \[ {R\left( x \right) } = {\left( {2000 - 50x} \right)\left( {1000 + 50x} \right) } = {2000000 - 50000x + 100000x - 2500{x^2} } = { - 2500{x^2} + 50000x + 2000000\;\;\text{(руб)}.} \] Дифференцируя функцию \(R\left( x \right),\) найдем точку экстремума: \[ {R'\left( x \right) } = {{\left( { - 2500{x^2} + 50000x + 2000000} \right)^\prime } } = { - 5000x + 50000;} \] \[ {R'\left( x \right) = 0,}\;\; {\Rightarrow - 5000x + 50000 = 0,}\;\; {\Rightarrow x = \frac{{50000}}{{5000}} = 10.} \] Заметим, что вторая производная функции \(R\left( x \right)\) отрицательна: \[ {R''\left( x \right) } = {{\left( { - 5000x + 50000} \right)^\prime } } = { - 5000 < 0.} \] Поэтому \(x = 10\) является точкой максимума. Следовательно, доход будет наибольшим, когда число вычетов равно \(x = 10.\) Цена изделия в этом случае составляет \[2000 - 50 \cdot 10 = 1500\;\;\text{(руб)},\] а объем продаж за месяц равен \[1000 + 50 \cdot 10 = 1500\;\;\text{(изделий)}.\] Соответственно, максимальный доход компании составляет \[{R_{\max }} = 1500 \cdot 1500 = 2225000\;\;\text{(руб)}.\]

   Пример 6

При плавании корабля расходы на топливо пропорциональны квадрату его скорости. Кроме этого существуют постоянные расходы, не зависящие от скорости и составляющие \(p\) (рублей/час). При какой скорости общие расходы на \(1\) км пути будут наименьшими? По условию задачи, переменная часть расходов зависит от скорости следующим образом: \[q = k{v^2},\] где \(k\) − коэффициент пропорциональности. Тогда суммарные расходы за один час выражаются формулой \[C = p + q = p + k{v^2}.\] За один час корабль проходит расстояние, равное \(v.\) Поэтому расходы на \(1\) км пути составляют \[ {{C_1} = {C_1}\left( v \right) } = {\frac{C}{v} } = {\frac{{p + k{v^2}}}{v} } = {\frac{p}{v} + kv.} \] Полученное выражение представляет собой функцию от скорости \(v.\) Исследуем ее на экстремум: \[ {{C'_1} \left( v \right) } = {{\left( {\frac{p}{v} + kv} \right)^\prime } } = { - \frac{p}{{{v^2}}} + k } = {\frac{{k{v^2} - p}}{{{v^2}}};} \] \[ {{C'_1} \left( v \right) = 0,}\;\; {\Rightarrow \frac{{k{v^2} - p}}{{{v^2}}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {k{v^2} - p = 0}\\ {{v^2} \ne 0} \end{array},}\;\; {\Rightarrow v = \sqrt {\frac{p}{k}} } \right..} \] При найденном значении \(v\) функция \({C_1} \left( v \right)\) достигает минимума, так как производная при переходе через эту точку меняет знак с минуса на плюс. Следовательно, при такой скорости расходы на \(1\) км пути будут наименьшими. Сумма расходов за \(1\) час при этом составляет \[ {C = p + k{v^2} } = {p + k{\left( {\sqrt {\frac{p}{k}} } \right)^2} = 2p,} \] т.е. равна удвоенным постоянным расходам.

   Пример 7

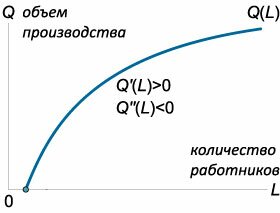
Зависимость объема производства \(Q\) от количества работников \(L\) описывается функцией \(Q\left( L \right)\) (рисунок \(1\)). Показать, что если производные удовлетворяют условиям \[Q'\left( L \right) > 0,\;\;\;Q''\left( L \right) < 0,\] то существует оптимальное число работников \({L^*},\) при котором прибыль будет наибольшей. Условия \(Q'\left( L \right) > 0,\;Q''\left( L \right) < 0,\) отражают снижение производительности труда при увеличении числа работников и часто встречаются на практике. Полагая, что расходы, связанные с работниками, пропорциональны их количеству, можно записать выражение для прибыли в виде \[ {P = P\left( L \right) } = {pQ\left( L \right) - qL - C,} \] где \(p\) − цена продажи единицы продукции, \(Q\left( L \right)\) − рассмотренный выше объем производства, \(qL\) − часть расходов, связанная с работниками, \(C\) − постоянная часть расходов, не зависящая от числа работников.

В данной формуле \(pQ\left( L \right)\) выражает доход предприятия за определенный период. В результате прибыль \(P\) представляет собой функцию от числа работников \(P\left( L \right).\)

Исследуем возможный экстремум этой функции. Первая производная имеет вид: \[ {P'\left( L \right) = {\left[ {pQ\left( L \right) - qL - C} \right]^\prime } } = {pQ'\left( L \right) - q.} \] Функция прибыли \(P\left( L \right)\) имеет критическую точку \({L^*}\) при условии \[ {pQ'\left( L \right) - q = 0,}\;\; {\Rightarrow Q'\left( L \right) = \frac{q}{p}.} \] Поскольку вторая производная отрицательна при всех допустимых значениях \(L,\) то критическая точка является точкой максимума. Таким образом, в заданной системе всегда существует оптимальное количество работников \({L^*},\) при котором прибыль предприятия максимальна.

   Пример 8

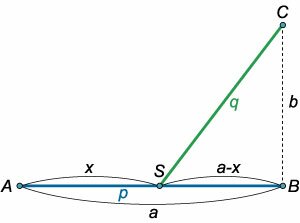
Города \(A\) и \(B\) находятся на расстоянии \(a\) км и соединены прямой железной дорогой. Для перевозки грузов из города \(A\) в город \(C,\) отстоящий от железной дороги на \(b\) км, необходимо построить автомобильную дорогу, примыкающую к железной дороге (рисунок \(2\)). К какой точке \(S\) следует провести шоссе, чтобы транспортировка грузов была наиболее экономичной? Стоимость перевозки \(1\) тонны груза на \(1\) км составляет \(p\) руб. по железной дороге и \(q\) руб. по автомобильной дороге. Обозначим через \(x\) расстояние от города \(A\) до автомобильного съезда \(S.\) Тогда стоимость перевозки \(1\) тонны груза по железнодорожному участку \(AS\) равна \(px.\) Длина автомобильного участка пути \(SC\) определяется по теореме Пифагора и составляет \[\left| {SC} \right| = \sqrt {{{\left( {a - x} \right)}^2} + {b^2}} .\] Соответственно, стоимость перевозки по этому автомобильному участку будет равна \[q\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} .\] Следовательно, полная стоимость транспортировки \(1\) тонны груза из пункта \(A\) в пункт \(C\) описывается функцией \[ {Q = Q\left( x \right) } = {px + q\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} .} \] Для исследования экстремальных значений функции \(Q\left( x \right)\) найдем ee производную: \[ {Q'\left( x \right) } = {{\left( {px + q\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} } \right)^\prime } } = {p + \frac{{q \cdot \left( { - 2} \right)\left( {a - x} \right)}}{{2\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} }} } = {p - \frac{{q\left( {a - x} \right)}}{{\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} }}.} \] Приравнивая производную нулю, вычисляем критическое значение \(x:\) \[ {Q'\left( x \right) = 0,}\;\; {\Rightarrow p - \frac{{q\left( {a - x} \right)}}{{\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} }} = 0,}\;\; {\Rightarrow \frac{{p\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} - q\left( {a - x} \right)}}{{\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} }} = 0,}\;\; {\Rightarrow p\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} - q\left( {a - x} \right) = 0,}\;\; {\Rightarrow p\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} = q\left( {a - x} \right),}\;\; {\Rightarrow {p^2}{\left( {a - x} \right)^2} + {p^2}{b^2} = {q^2}{\left( {a - x} \right)^2},}\;\; {\Rightarrow \left( {{q^2} - {p^2}} \right){\left( {a - x} \right)^2} = {p^2}{b^2},}\;\; {\Rightarrow a - x = \frac{{pb}}{{\sqrt {{q^2} - {p^2}} }},}\;\; {\Rightarrow x = a - \frac{{pb}}{{\sqrt {{q^2} - {p^2}} }} } = {a - \frac{b}{{\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} }}.} \] Посмотрим как изменяется знак производной при переходе через найденное критическое значение. В выражении для производной в виде \[ {Q'\left( x \right) } = {p - \frac{{q\left( {a - x} \right)}}{{\sqrt {{{\left( {a - x} \right)}^2} + {b^2}} }} } \] числитель дроби при уменьшении или увеличении \(x\) изменяется больше, чем знаменатель. Поэтому в левой окрестности критической точки производная будет отрицательной, а в правой окрестности − положительной. Таким образом, данная точка соответствует минимуму функции \(Q\left( x \right).\)

Заметим, что найденное решение является действительным лишь при условии \(q > p,\) т.е. удельные расходы по перевозке грузов по автомобильной дороге должны превышать расходы при транспортировке по железной дороге. Это условие, однако, не является единственным ограничением на возможные значения \(p\) и \(q.\) Исследуя диапазон значений, в котором может изменяться отношение \(\large\frac{q}{p}\normalsize\) рассмотрим два предельных случая:

Если \(x = 0,\) то получаем следующее решение: \[ {a - \frac{b}{{\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} }} = 0,}\;\; {\Rightarrow \frac{{a\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} - b}}{{\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} }} = 0,}\;\; {\Rightarrow a\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} = b,}\;\; {\Rightarrow {\left( {\frac{q}{p}} \right)^2} - 1 = {\left( {\frac{b}{a}} \right)^2},}\;\; {\Rightarrow \frac{q}{p} = \sqrt {{{\left( {\frac{b}{a}} \right)}^2} + 1} .} \] Это отношение удельных расходов \(\large\frac{q}{p}\normalsize\) является минимально возможным. При этом значении \(\large\frac{q}{p}\normalsize\) надо строить автомобильную дорогу сразу вдоль диагонали \(AC.\)

Другой предельный случай соответствует решению \(x = a:\) \[ {a - \frac{b}{{\sqrt {{{\left( {\frac{q}{p}} \right)}^2} - 1} }} = a,}\;\; {\Rightarrow \frac{q}{p} \to \infty .} \] Здесь отношение \(\large\frac{q}{p}\normalsize\) стремится к бесконечности. Ясно, что на практике указанное отношение является конечным, т.е. оптимальная точка ответвления всегда будет находиться в промежутке \(0 \le x < a.\)