|
|
|
|
Четные и нечетные продолжения
|
|
Предположим, что \(f\left( x \right)\) является кусочно-непрерывной функцией, заданной в интервале \(\left[ {0,\pi } \right].\) Чтобы найти разложение данной функции в ряд Фурье, нужно продолжить ее и построить в интервале \(\left[ {-\pi,\pi } \right].\) Это можно сделать двумя способами:
-
можно построить четное продолжение \(f\left( x \right):\) \[ {f_\text{четн}}\left( x \right) = \begin{cases} f\left( {-x} \right), & -\pi \le x \lt 0 \\ f\left( {x} \right), & 0 \le x \le \pi \end{cases}, \]
-
или построить нечетное продолжение \(f\left( x \right):\) \[ {f_\text{нечетн}}\left( x \right) = \begin{cases} -f\left( {-x} \right), & -\pi \le x \lt 0 \\ f\left( {x} \right), & 0 \le x \le \pi \end{cases}. \]
В случае четной функции разложение в ряд Фурье описывается выражением \[{f_\text{четн}}\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} ,\] где \[ {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} ,}\;\; {n = 0,1,2,3, \ldots } \] В случае нечетной функции, соответственно, получаем \[{f_\text{нечетн}}\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin nx} ,\] где коэффициенты разложения равны \[ {{b_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\sin nxdx} ,}\;\; {n = 1,2,3, \ldots } \] Понятие четного и нечетного продолжения функции можно ввести и для непериодической функции. Пусть функция \(f\left( x \right)\) определена в интервале \(\left[ {0,L } \right].\) Используя четное продолжение данной функции на интервал \(\left[ {-L,L } \right],\) получим следующую формулу разложения в ряд Фурье: \[{f_\text{четн}}\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos \frac{{n\pi x}}{L}} ,\] где \[ {{a_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} ,}\;\; {n = 0,1,2,3, \ldots } \] В случае нечетного продолжения соответствующая формула имеет вид \[{f_\text{нечетн}}\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin \frac{{n\pi x}}{L}} ,\] где коэффициенты \({b_n}\) равны \[ {{b_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\sin \frac{{n\pi x}}{L}dx} ,}\;\; {n = 1,2,3, \ldots } \]
|
|
Пример 1
|
|
Разложить по четным гармоникам функцию \[ f\left( x \right) = \begin{cases} 1, & 0 \le x \le d \\ 0, & d < x \le \pi \end{cases}. \]
Решение.
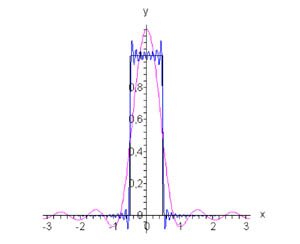
Разложить функцию по четным гармоникам − это значит построить четное продолжение заданной функции. Соответствующий ряд Фурье будет иметь вид \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} .\] Вычислим коэффициенты \({a_0}\) и \({a_n}:\) \[{a_0} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)dx} = \frac{2}{\pi }\int\limits_0^d {dx} = \frac{{2d}}{\pi },\] \[ {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^d {\cos nxdx} } = {\frac{2}{{n\pi }}\left[ {\left. {\left( {\sin nx} \right)} \right|_0^d} \right] } = {\frac{2}{{n\pi }}\sin nd.} \] Таким образом, разложение ступенчатой функции в ряд Фурье по четным гармоникам определяется выражением \[f\left( x \right) = \frac{d}{\pi } + \frac{2}{\pi }\sum\limits_{n = 1}^\infty {\frac{{\sin nd}}{n}\cos nx} .\] График данной функции и Фурье аппроксимации для случаев \(n = 5\) и \(n = 50\) приводятся на рисунке \(1.\)
|
|
|
|
|
Рис.1, d = 0.5, n = 5, n = 50
|
|
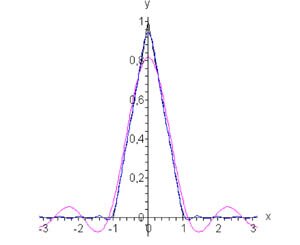
Рис.2, d = 1, n = 3, n = 10
|
|
|
Пример 2
|
|
Построить разложение в ряд Фурье по четным гармоникам для функции \[ f\left( x \right) = \begin{cases} 1 - \frac{x}{d}, & 0 \le x \le d \\ 0, & d < x \le \pi \end{cases}. \]
Решение.
Используя четное продолжение первоначально заданной функции, можно записать \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} .\] Коэффициенты Фурье \({a_0}\) и \({a_n}\) имеют значения: \[ {{a_0} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)dx} } = {\frac{2}{\pi }\int\limits_0^d {\left( {1 - \frac{x}{d}} \right)dx} } = {\frac{2}{\pi }\left[ {\left. {\left( {x - \frac{{{x^2}}}{{2d}}} \right)} \right|_0^d} \right] } = {\frac{2}{\pi } \cdot \frac{d}{2} = \frac{d}{\pi },} \] \[ {{a_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^d {\left( {1 - \frac{x}{d}} \right)\cos nxdx} } = {\frac{2}{\pi }\int\limits_0^d {\cos nxdx} - \frac{2}{{\pi d}}\int\limits_0^d {x\cos nxdx} } = {\frac{2}{{n\pi }}\left. {\left( {\sin nx} \right)} \right|_0^d } - {\frac{2}{{\pi d}}\left[ {\left. {\left( {\frac{{x\sin nx}}{n}} \right)} \right|_0^d - \frac{1}{n}\int\limits_0^d {\sin nxdx} } \right] } = {\frac{2}{{n\pi }}\left. {\left( {\sin nx} \right)} \right|_0^d } - {\frac{2}{{n\pi d}}\left. {\left( {x\sin nx} \right)} \right|_0^d } - {\frac{2}{{{n^2}\pi d}}\left. {\left( {\cos nx} \right)} \right|_0^d } = {\frac{2}{{n\pi }}\left[ {\sin nd - \frac{{d\sin nd}}{d} - \frac{1}{{nd}}\left( {\cos nd - 1} \right)} \right] } = {\frac{2}{{{n^2}\pi d}}\left( {\cos nd - 1} \right) } = {\frac{4}{{{n^2}\pi d}}\,{\sin ^2}\frac{{nd}}{2}.} \] Следовательно, Фурье разложение по четным гармоникам имеет вид (рисунок \(2\)): \[f\left( x \right) = \frac{d}{{2\pi }} + \frac{4}{{\pi d}}\sum\limits_{n = 1}^\infty {\frac{{{{\sin }^2}\frac{{nd}}{2}}}{{{n^2}}}\cos nx} .\]
|
|
Пример 3
|
|
Построить нечетное продолжение функции \(f\left( x \right) = \cos x,\) заданной в интервале \(\left[ {0,\pi } \right].\)
Решение.
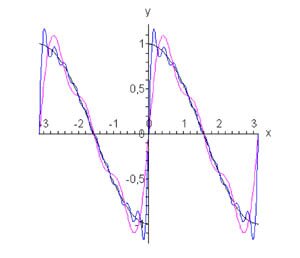
Поскольку мы применяем нечетное продолжение, разложение в ряд Фурье будет иметь вид \[f\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin nx} .\] Коэффициенты \({{b_n}}\) равны \[ {{b_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\sin nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {\cos x\sin nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {\left[ {\sin \left( {nx + x} \right) + \sin \left( {nx - x} \right)} \right]dx} } = { - \frac{1}{\pi }\left[ {\left. {\left( {\frac{{\cos \left( {n + 1} \right)x}}{{n + 1}} + \frac{{\cos \left( {n - 1} \right)x}}{{n - 1}}} \right)} \right|_0^\pi } \right] } = { - \frac{1}{\pi }\left[ {\frac{{\cos \left( {n + 1} \right)\pi }}{{n + 1}} - \frac{1}{{n + 1}} + \frac{{\cos \left( {n - 1} \right)\pi }}{{n - 1}} - \frac{1}{{n - 1}}} \right] } = { - \frac{1}{\pi }\left[ {\frac{{{{\left( { - 1} \right)}^{n + 1}} - 1}}{{n + 1}} + \frac{{{{\left( { - 1} \right)}^{n - 1}} - 1}}{{n - 1}}} \right] } = {\frac{1}{\pi }\left[ {1 + {{\left( { - 1} \right)}^n}} \right] \cdot \frac{{2n}}{{{n^2} - 1}} } = {\frac{{2n}}{\pi } \cdot \frac{{1 + {{\left( { - 1} \right)}^n}}}{{{n^2} - 1}}.} \] Здесь мы учли, что \[{\left( { - 1} \right)^{n + 1}} = {\left( { - 1} \right)^{n - 1}} = - {\left( { - 1} \right)^n}.\] Найденное выражение для коэффициентов \({b_n}\) верно при \(n \ge 2.\) Если \(n = 1,\) то получаем \[ {{b_1} = \frac{2}{\pi }\int\limits_0^\pi {\cos x\sin xdx} } = {\frac{1}{\pi }\int\limits_0^\pi {\sin 2xdx} } = {\frac{1}{\pi }\left[ {\left. {\left( { - \frac{{\cos 2x}}{2}} \right)} \right|_0^\pi } \right] } = { - \frac{1}{{2\pi }}\left( {\cos 2\pi - \cos 0} \right) = 0.} \] Кроме того, можно заметить, что \({b_{2k + 1}} = 0\) для нечетных \(n = 2k + 1.\) Для четных значений индекса \(n = 2k\) справедливо выражение \[{b_{2k}} = \frac{{4k}}{\pi } \cdot \frac{2}{{4{k^2} - 1}} = \frac{{8k}}{{\pi \left( {4{k^2} - 1} \right)}}.\] Таким образом, разложение в ряд Фурье по нечетным гармоникам имеет вид (рисунок \(3\)): \[f\left( x \right) = \frac{8}{\pi }\sum\limits_{k = 1}^\infty {\frac{k}{{4{k^2} - 1}}\sin 2kx} .\]
|
|
|
|
|
Рис.3, n = 3, n = 10
|
|
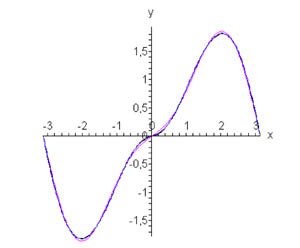
Рис.4, n = 1, n = 2
|
|
|
Пример 4
|
|
Построить нечетное продолжение функции \(f\left( x \right) = x\sin x,\) заданной в интервале \(\left[ {0,\pi } \right].\)
Решение.
Для нечетного продолжения ряд Фурье записывается в виде \[f\left( x \right) = x\sin x = \sum\limits_{n = 1}^\infty {{b_n}\sin nx} .\] Найдем коэффициенты \({b_n}:\) \[ {{b_n} = \frac{2}{\pi }\int\limits_0^\pi {f\left( x \right)\sin nxdx} } = {\frac{2}{\pi }\int\limits_0^\pi {x\sin x\sin nxdx} } = {\frac{1}{\pi }\int\limits_0^\pi {x\left[ {\cos \left( {nx - x} \right) - \cos\left( {nx + x} \right)} \right]dx} } = {\frac{1}{\pi }\int\limits_0^\pi {\left[ {x\cos \left( {n - 1} \right)x - x\cos\left( {n + 1} \right)x} \right]dx} .} \] Применяя интегрирование по частям, получаем \[ {{b_n} = \frac{1}{\pi }\left[ {\left. {\left( {\frac{{x\sin \left( {n - 1} \right)x}}{{n - 1}}} \right)} \right|_0^\pi } \right. } - \;{\frac{1}{{n - 1}}\int\limits_0^\pi {\sin \left( {n - 1} \right)xdx} } - {\left. {\left( {\frac{{x\sin \left( {n + 1} \right)x}}{{n + 1}}} \right)} \right|_0^\pi } + \;{\left. {\frac{1}{{n + 1}}\int\limits_0^\pi {\sin \left( {n + 1} \right)xdx} } \right] } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{x\sin \left( {n - 1} \right)x}}{{n - 1}}} \right)} \right|_0^\pi } \right. } + {\left. {\left( {\frac{{\cos\left( {n - 1} \right)x}}{{{{\left( {n - 1} \right)}^2}}}} \right)} \right|_0^\pi } - {\left. {\left( {\frac{{x\sin \left( {n + 1} \right)x}}{{n + 1}}} \right)} \right|_0^\pi } + {\left. {\left. {\left( {\frac{{\cos\left( {n + 1} \right)x}}{{{{\left( {n + 1} \right)}^2}}}} \right)} \right|_0^\pi } \right] } = {\frac{1}{\pi }\left[ {\frac{{\pi \sin \left( {n - 1} \right)\pi }}{{n - 1}}} \right. } + {\frac{{\cos \left( {n - 1} \right)\pi - 1}}{{{{\left( {n - 1} \right)}^2}}} } - {\frac{{\pi \sin \left( {n + 1} \right)\pi }}{{n + 1}} } - {\left. {\frac{{\cos \left( {n + 1} \right)\pi - 1}}{{{{\left( {n + 1} \right)}^2}}}} \right].} \] Поскольку \[ {\sin \left( {n - 1} \right)\pi = \sin \left( {n + 1} \right)\pi = 0\;\;\text{и}\;\;} {\cos \left( {n - 1} \right)\pi = \cos \left( {n + 1} \right)\pi = {\left( { - 1} \right)^{n + 1}},} \] то выражение для коэффициентов \({b_n}\) упрощается: \[ {{b_n} = \frac{1}{\pi }\left[ {\frac{{{{\left( { - 1} \right)}^{n + 1}} - 1}}{{{{\left( {n - 1} \right)}^2}}} - \frac{{{{\left( { - 1} \right)}^{n + 1}} - 1}}{{{{\left( {n + 1} \right)}^2}}}} \right] } = {\frac{1}{\pi }\left( {{{\left( { - 1} \right)}^{n + 1}} - 1} \right)\left( {\frac{1}{{{{\left( {n - 1} \right)}^2}}} - \frac{1}{{{{\left( {n + 1} \right)}^2}}}} \right) } = {\frac{1}{\pi }\left( {{{\left( { - 1} \right)}^{n + 1}} - 1} \right)\frac{{4n}}{{{{\left( {{n^2} - 1} \right)}^2}}}.} \] Последняя формула верна при \(n \ge 2.\) Заметим, что для четных \(n = 2k,\) \({b_{2k}} = - \large\frac{{16k}}{{\pi {{\left( {4{k^2} - 1} \right)}^2}}}\normalsize,\) а для нечетных \(n = 2 k + 1,\) \({b_{2k + 1}} = 0,\) где \(k = 1,2,3, \ldots\)
Вычислим отдельно \({b_1}:\) \[ {{b_1} = \frac{2}{\pi }\int\limits_0^\pi {x\sin x\sin xdx} } = {\frac{2}{\pi }\int\limits_0^\pi {x{{\sin }^2}xdx} } = {\frac{1}{\pi }\int\limits_0^\pi {x\left( {1 - \cos 2x} \right)dx} } = {\frac{1}{\pi }\int\limits_0^\pi {\left( {x - x\cos 2x} \right)dx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^\pi - \left. {\left( {\frac{{x\sin 2x}}{2}} \right)} \right|_0^\pi + \frac{1}{2}\int\limits_0^\pi {\sin 2xdx} } \right] } = {\frac{1}{{2\pi }}\left[ {\left. {\left( {{x^2} - x\sin 2x - \frac{{\cos 2x}}{2}} \right)} \right|_0^\pi } \right] } = {\frac{1}{{2\pi }}\left( {{\pi ^2} - \pi \sin 2\pi - \frac{{\cos 2\pi }}{2} + \frac{1}{2}} \right) } = {\frac{\pi }{2}.} \] Итак, разложение в ряд Фурье по нечетным гармоникам определяется формулой \[ {f\left( x \right) = x\sin x } = {\frac{\pi }{2}\sin x - \frac{{16}}{\pi }\sum\limits_{k = 1}^\infty {\frac{k}{{{{\left( {4{k^2} - 1} \right)}^2}}}\sin 2kx} .} \] На рисунке \(4\) показана исходная функция и ее Фурье аппроксимации при \(n = 1\) и \(n = 2.\)
|
|
|
|