Физические приложения криволинейных интегралов

С помощью криволинейных интегралов вычисляются

• Масса кривой;

• Центр масс и моменты инерции кривой;

• Работа при перемещении тела в силовом поле;

• Магнитное поле вокруг проводника с током (Закон Ампера);

• Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).

Рассмотрим эти приложения более подробно с примерами.

Предположим, что кусок проволоки описывается некоторой пространственной кривой \(C.\) Пусть масса распределена вдоль этой кривой с плотностью \(\rho \left( {x,y,z} \right).\) Тогда общая масса кривой выражается через криволинейный интеграл первого рода \[m = \int\limits_C {\rho \left( {x,y,z} \right)ds} .\] Если кривая \(C\) задана в параметрическом виде с помощью векторной функции \(\mathbf{r}\left( t \right) = \left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right),\) то ее масса описывается формулой \[ m = {\int\limits_\alpha ^\beta {\rho \left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2} + {{\left( {\frac{{dz}}{{dt}}} \right)}^2}} dt} .} \] В случае плоской кривой, заданной в плоскости \(Oxy,\) масса определяется как \[m = \int\limits_C {\rho \left( {x,y} \right)ds}\] или в параметрической форме \[ m = {\int\limits_\alpha ^\beta {\rho \left( {x\left( t \right),y\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt} .} \] Пусть снова кусок проволоки описывается некоторой кривой \(C,\) а распределение массы вдоль кривой задано непрерывной функцией плотности \(\rho \left( {x,y,z} \right).\) Тогда координаты центра масс кривой определяются формулами \[\bar x = \frac{{{M_{yz}}}}{m},\;\;\bar y = \frac{{{M_{xz}}}}{m},\;\;\bar z = \frac{{{M_{xy}}}}{m},\] где \[ {{M_{yz}} = \int\limits_C {x\rho \left( {x,y,z} \right)ds} ,}\;\; {{M_{xz}} = \int\limits_C {y\rho \left( {x,y,z} \right)ds} ,}\;\; {{M_{xy}} = \int\limits_C {z\rho \left( {x,y,z} \right)ds} } \] − так называемые моменты первого порядка.

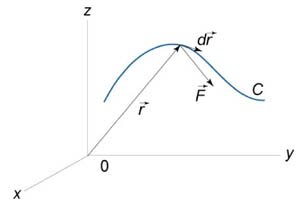
Моменты инерции относительно осей \(Ox, Oy\) и \(Oz\) определяются формулами \[ {{I_x} = \int\limits_C {\left( {{y^2} + {z^2}} \right)\rho \left( {x,y,z} \right)ds} ,}\;\; {{I_y} = \int\limits_C {\left( {{x^2} + {z^2}} \right)\rho \left( {x,y,z} \right)ds} ,}\;\; {{I_z} = \int\limits_C {\left( {{x^2} + {y^2}} \right)\rho \left( {x,y,z} \right)ds} .} \] Работа при перемещении тела в силовом поле \(\mathbf{F}\) вдоль кривой \(C\) выражается через криволинейный интеграл второго рода \[W = \int\limits_C {\mathbf{F} \cdot d\mathbf{r}} ,\] где \(\mathbf{F}\) − сила, действующая на тело, \(d\mathbf{r}\) − единичный касательный вектор (рисунок \(1\)). Обозначение \({\mathbf{F} \cdot d\mathbf{r}}\) означает скалярное произведение векторов \(\mathbf{F}\) и \(d\mathbf{r}.\)

Заметим, что силовое поле \(\mathbf{F}\) не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы \(\mathbf{F}\) иногда может оказаться отрицательной.

Если векторное поле задано в координатной форме в виде \[\mathbf{F} = \left( {P\left( {x,y,z} \right),Q\left( {x,y,z} \right),R\left( {x,y,z} \right)} \right),\] то работа поля вычисляется по формуле \[W = \int\limits_C {\mathbf{F} \cdot d\mathbf{r}} = \int\limits_C {Pdx + Qdy + Rdz} .\] В частном случае, когда тело двигается вдоль плоской кривой \(C\) в плоскости \(Oxy,\) справедлива формула \[W = \int\limits_C {\mathbf{F} \cdot d\mathbf{r}} = \int\limits_C {Pdx + Qdy},\] где \(\mathbf{F} = \left( {P\left( {x,y} \right),Q\left( {x,y} \right)} \right).\)

Если траектория движения \(C\) определена через параметр \(t\) (\(t\) часто означает время), то формула для вычисления работы принимает вид \[ W = {\int\limits_\alpha ^\beta {\left[ {P\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dx}}{{dt}} + Q\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dy}}{{dt}} + R\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dz}}{{dt}}} \right]dt} ,} \] где \(t\) изменяется в интервале от \(\alpha\) до \(\beta.\)

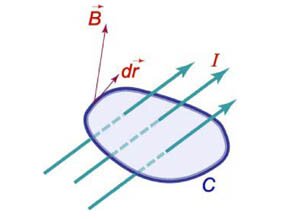
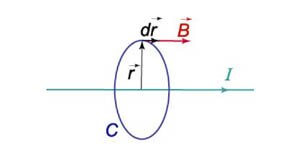
Если векторное поле \(\mathbf{F}\) потенциально, то работа по перемещению тела из точки \(A\) в точку \(B\) выражается формулой \[W = u\left( B \right) - u\left( A \right),\] где \(u\left( {x,y,z} \right)\) − потенциал поля. Криволинейный интеграл от магнитного поля с индукцией \(\mathbf{B}\) вдоль замкнутого контура \(C\) пропорционален полному току, протекающему через область, ограниченную контуром \(C\) (рисунок \(2\)). Это выражается формулой \[\int\limits_C {\mathbf{B} \cdot d\mathbf{r}} = {\mu _0}I,\] где \({\mu _0}\) − магнитная проницаемость ваккуума, равная \(1,26 \times {10^{ - 6}}\,\text{Н/м}.\)

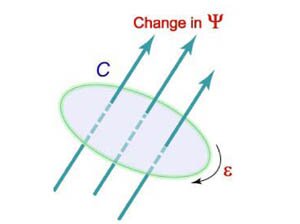
Электродвижущая сила \(\varepsilon,\) наведенная в замкнутом контуре \(C,\) равна скорости изменения магнитного потока \(\psi,\) проходящего через данный контур (рисунок \(3\)). \[\varepsilon = \int\limits_C {\mathbf{E} \cdot d\mathbf{r}} = - \frac{{d\psi }}{{dt}}.\]

   Пример 1

Определить массу проволоки, имеющей форму отрезка от точки \(A\left( {1,1} \right)\) до \(B\left( {2,4} \right).\) Масса распределена вдоль отрезка с плотностью \(\rho \left( {x,y} \right) = 3x + 2y.\) Составим сначала параметрическое уравнение прямой \(AB.\) \[ {\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = t,}\;\; {\Rightarrow \frac{{x - 1}}{{2 - 1}} = \frac{{y - 1}}{{4 - 1}} = t,}\;\; {\Rightarrow \frac{{x - 1}}{1} = \frac{{y - 1}}{3} = t}\;\; {\text{или}\;\;\left\{ {\begin{array}{*{20}{l}} {x = t + 1}\\ {y = 3t + 1} \end{array}} \right.,} \] где параметр \(t\) изменяется в интервале \(\left[ {0,1} \right].\) Тогда масса проволоки равна \[ {m = \int\limits_\alpha ^\beta {\rho \left( {x\left( t \right),y\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^1 {\left( {3x\left( t \right) + 2y\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^1 {\left( {3\left( {t + 1} \right) + 2\left( {3t + 1} \right)} \right)\sqrt {{{\left( {\frac{{d\left( {t + 1} \right)}}{{dt}}} \right)}^2} + {{\left( {\frac{{d\left( {3t + 1} \right)}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^1 {\left( {9t + 5} \right)\sqrt {{1^2} + {3^2}} dt} } = {\sqrt {10} \int\limits_0^1 {\left( {9t + 5} \right)dt} } = {\sqrt {10} \left[ {\left. {\left( {\frac{{9{t^2}}}{2} + 5t} \right)} \right|_0^1} \right] } = {\frac{{19\sqrt {10} }}{2} \approx 30.} \]

   Пример 2

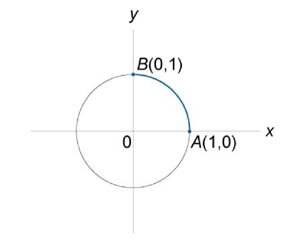
Определить массу проволоки, имеющей форму дуги окружности \({x^2} + {y^2} = 1\) от точки \(A\left( {1,0} \right)\) до \(B\left( {0,1} \right)\) с плотностью \(\rho \left( {x,y} \right) = xy\) (рисунок \(4\)). Окружность радиусом \(1\) с центром в начале координат описывается параметрическими уравнениями \[x = \cos t,\;\;y = \sin t,\] где параметр \(t\) изменяется в диапазоне \(\left[ {0,\large\frac{\pi }{2}\normalsize} \right].\) Тогда масса данного куска проволоки вычисляется следующим образом: \[ {m = \int\limits_\alpha ^\beta {\rho \left( {x\left( t \right),y\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {x\left( t \right)y\left( t \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos t\sin t\sqrt {{{\left( {\frac{{d\cos t}}{{dt}}} \right)}^2} + {{\left( {\frac{{d\sin t}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos t\sin t\sqrt {{{\left( { - \sin t} \right)}^2} + {{\left( {\cos t} \right)}^2}} dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos t\sin tdt} } = {\frac{1}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin 2tdt} } = {\frac{1}{4}\left[ {\left. {\left( { - \cos 2t} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{1}{4}\left( { - \cos \pi + \cos 0} \right) } = {\frac{1}{2}.} \]

   Пример 3

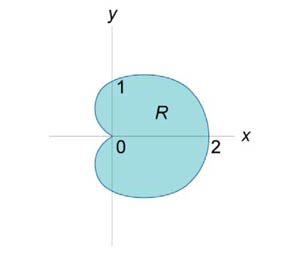
Найти центр масс проволоки, имеющей форму кардиоиды \(r = {1 + \cos \theta } \) (рисунок \(5\)), с плотностью \(\rho = 1.\) Очевидно, в силу симметрии, \(\bar y = 0.\) Чтобы найти координату центра масс \(\bar x,\) достаточно рассмотреть верхнюю половину кардиоиды.

Предварительно найдем полную массу кардиоиды. В полярных координатах получаем \[ {m = \int\limits_\alpha ^\beta {\rho \left( {r,\theta } \right)\sqrt {{r^2} + {{\left( {\frac{{dr}}{{d\theta }}} \right)}^2}} d\theta } } = {\int\limits_0^\pi {1 \cdot \sqrt {{{\left( {1 + \cos \theta } \right)}^2} + {{\left( { - \sin \theta } \right)}^2}} d\theta } } = {\int\limits_0^\pi {\sqrt {1 + 2\cos \theta + {{\cos }^2}\theta + {{\sin }^2}\theta } d\theta } } = {\int\limits_0^\pi {\sqrt {2 + 2\cos \theta } d\theta } } = {\sqrt 2 \int\limits_0^\pi {\sqrt {1 + \cos \theta } d\theta } } = {\sqrt 2 \int\limits_0^\pi {\sqrt {2{{\left( {\cos \frac{\theta }{2}} \right)}^2}} d\theta } } = {4\int\limits_0^\pi {\cos \frac{\theta }{2}d\left( {\frac{\theta }{2}} \right)} } = {4\left[ {\left. {\left( {\sin \frac{\theta }{2}} \right)} \right|_0^\pi } \right] = 4.} \] Вычислим момент первого порядка \({M_y}.\) Используя формулу \[ {\int\limits_C {F\left( {x,y} \right)ds} } = {\int\limits_\alpha ^\beta {F\left( {r\cos \theta ,r\sin \theta } \right)\sqrt {{r^2} + {{\left( {\frac{{dr}}{{d\theta }}} \right)}^2}} d\theta } ,} \] находим \[ {{M_y} = \int\limits_C {xds} } = {\int\limits_0^\pi {r\cos \theta \sqrt {{r^2} + {{\left( {\frac{{dr}}{{d\theta }}} \right)}^2}} d\theta } } = {\int\limits_0^\pi {\left( {1 + \cos \theta } \right)\cos \theta \sqrt {{{\left( {1 + \cos \theta } \right)}^2} + {{\sin }^2}\theta } d\theta } } = {\int\limits_0^\pi {\left( {1 + \cos \theta } \right)\cos \theta \sqrt {1 + 2\cos \theta + {{\cos }^2}\theta + {{\sin }^2}\theta } d\theta } } = {\sqrt 2 \int\limits_0^\pi {\left( {1 + \cos \theta } \right)\cos \theta \sqrt {1 + \cos \theta } d\theta } } = {2\sqrt 2 \int\limits_0^\pi {2{{\left( {\cos \frac{\theta }{2}} \right)}^2}\left( {2{{\left( {\cos \frac{\theta }{2}} \right)}^2} - 1} \right)\sqrt {2{{\left( {\cos \frac{\theta }{2}} \right)}^2}} d\left( {\frac{\theta }{2}} \right)} } = {8\int\limits_0^\pi {{{\left( {\cos \frac{\theta }{2}} \right)}^3}\left( {2{{\left( {\cos \frac{\theta }{2}} \right)}^2} - 1} \right)d\left( {\frac{\theta }{2}} \right)} .} \] Полагая \(\large\frac{\theta }{2}\normalsize = z\) (нижний и верхний пределы интегрирования становятся равными, соответственно, \(0\) и \(\large\frac{\pi }{2}\normalsize ,\)) можно записать \[ {{M_y} = 16\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^5}zdz} - 8\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^3}zdz} } = {16\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^4}zd\left( {\sin z} \right)} - 8\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}zd\left( {\sin z} \right)} } = {16\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\left( {1 - {\sin^2}z} \right)}^2}d\left( {\sin z} \right)} } - {8\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 - {\sin^2}z} \right)d\left( {\sin z} \right)} } = {16\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 - 2{\sin^2}z + {\sin^4}z} \right)d\left( {\sin z} \right)} } - {8\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 - {\sin^2}z} \right)d\left( {\sin z} \right)} } = {16\left[ {\left. {\left( {\sin z - \frac{{2{{\sin }^3}z}}{3} + \frac{{{{\sin }^5}z}}{5}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } - {8\left[ {\left. {\left( {\sin z - \frac{{{{\sin }^3}z}}{3}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {16\left( {1 - \frac{2}{3} + \frac{1}{5}} \right) - 8\left( {1 - \frac{1}{3}} \right) } = {\frac{{16}}{5}.} \] Тогда \[\bar x = \frac{{{M_y}}}{m} = \frac{{\frac{{16}}{5}}}{4} = \frac{4}{5}.\] Следовательно, координаты центра масс кардиоиды равны \(\left( {0,\large\frac{4}{5}\normalsize} \right).\)

   Пример 4

Вычислить момент инерции \({I_x}\) проволоки в форме окружности \({x^2} + {y^2} = {a^2}\) с плотностью \(\rho = 1.\) Уравнения окружности в параметрической форме имеют вид \[\left\{ \begin{array}{l} x = a\cos t\\ y = a\sin t \end{array} \right.,\;\;0 \le t \le 2\pi .\] Момент инерции \({I_x}\) относительно оси \(Ox\) вычисляется по формуле \[ {{I_x} = \int\limits_C {{y^2}\rho ds} } = {\int\limits_0^{2\pi } {{{\left( {y\left( t \right)} \right)}^2}\rho \left( {x\left( t \right),y\left( t \right)} \right)\sqrt {{{\left( {\frac{{dx}}{{dt}}} \right)}^2} + {{\left( {\frac{{dy}}{{dt}}} \right)}^2}} dt.} } \] Проводя вычисления, получаем \[ {{I_x} = \int\limits_0^{2\pi } {{{\left( {a\sin t} \right)}^2} \cdot 1 \cdot \sqrt {{{\left( {\frac{{d\left( {a\cos t} \right)}}{{dt}}} \right)}^2} + {{\left( {\frac{{d\left( {a\sin t} \right)}}{{dt}}} \right)}^2}} dt} } = {\int\limits_0^{2\pi } {{a^2}{{\sin }^2}t\sqrt {{{\left( { - a\sin t} \right)}^2} + {{\left( {a\cos t} \right)}^2}} dt} } = {\int\limits_0^{2\pi } {{a^3}{{\sin }^2}t\sqrt {{{\sin }^2}t + {{\cos }^2}t} dt} } = {{a^3}\int\limits_0^{2\pi } {{{\sin }^2}t\,dt} } = {{a^3}\int\limits_0^{2\pi } {\frac{{1 - \cos 2t}}{2}dt} } = {\frac{{{a^3}}}{2}\int\limits_0^{2\pi } {\left( {1 - \cos 2t} \right)dt} } = {\frac{{{a^3}}}{2}\left[ {\left. {\left( {t - \frac{{\sin 2t}}{2}} \right)} \right|_0^{2\pi }} \right] } = {\frac{{{a^3}}}{2}\left( {2\pi - 0} \right) } = {\pi {a^3}.} \]

   Пример 5

Найти работу, совершаемую полем \(\mathbf{F}\left( {x,y} \right) = \left( {xy,x + y} \right)\) при перемещении тела от начала координат \(O\left( {0,0} \right)\) до точки \(A\left( {1,1} \right)\) по траектории \(C,\) где

1. \(C\) − отрезок прямой \(y = x;\)

2. \(C\) − кривая \(y = \sqrt x.\)

\(1.\;\;\) Вычислим работу при перемещении вдоль прямой \(y = x.\) \[ {{W_1} = \int\limits_C {\mathbf{F} \cdot d\mathbf{r}} } = {\int\limits_C {Pdx + Qdy} } = {\int\limits_C {xydx + \left( {x + y} \right)dy} } = {\int\limits_0^1 {x \cdot xdx + \left( {x + x} \right)dx} } = {\int\limits_0^1 {\left( {{x^2} + 2x} \right)dx} } = {\left. {\left( {\frac{{{x^3}}}{3} + {x^2}} \right)} \right|_0^1 } = {\frac{1}{3} + 1 = \frac{4}{3}.} \] \(2.\;\;\) Определим теперь работу при перещении вдоль кривой \(y = \sqrt x.\) \[ {{W_2} = \int\limits_C {\mathbf{F} \cdot d\mathbf{r}} } = {\int\limits_C {Pdx + Qdy} } = {\int\limits_C {xydx + \left( {x + y} \right)dy} } = {\int\limits_0^1 {x \cdot \sqrt x dx + \left( {x + \sqrt x } \right)\frac{{dx}}{{2\sqrt x }}} } = {\int\limits_0^1 {\left( {{x^{\large\frac{3}{2}\normalsize}} + \frac{{{x^{\large\frac{1}{2}\normalsize}}}}{2} + \frac{1}{2}} \right)dx} } = {\left. {\left( {\frac{{{x^{\large\frac{5}{2}\normalsize}}}}{{\frac{5}{2}}} + \frac{{{x^{\large\frac{3}{2}\normalsize}}}}{{2 \cdot \frac{3}{2}}} + \frac{x}{2}} \right)} \right|_0^1 } = {\frac{2}{5} + \frac{1}{3} + \frac{1}{2} } = {\frac{{37}}{{30}}.} \]

   Пример 6

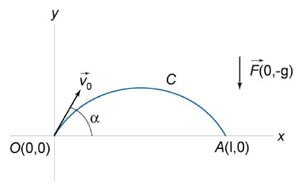
Тело массой \(m\) брошено под углом к горизонту \(\alpha\) с начальной скоростью \({v_0}\) (рисунок \(6\)). Вычислить работу силы притяжения \(\mathbf{F} = m\mathbf{g}\) за время движения тела до момента соударения с землей. Запишем закон движения тела в параметрической форме. \[x = {v_{0x}}t = {v_0}\cos \alpha \cdot t,\] \[y = {v_{0y}}t - \frac{{g{t^2}}}{2} = {v_0}\sin\alpha \cdot t - \frac{{g{t^2}}}{2}.\] При соударении с землей \(y = 0,\) так что время полета тела равно \[ {{v_0}\sin\alpha \cdot t - \frac{{g{t^2}}}{2} = 0,}\;\; {\Rightarrow t\left( {{v_0}\sin\alpha - \frac{{gt}}{2}} \right) = 0,}\;\; {\Rightarrow t = \frac{{2{v_0}\sin\alpha }}{g}.} \] Силу притяжения запишем в виде \(\mathbf{F} = m\mathbf{g} = m\left( {0, - g} \right).\) Тогда работа за время перемещения тела равна \[ {W = \int\limits_\alpha ^\beta {\left( {P\frac{{dx}}{{dt}} + Q\frac{{dy}}{{dt}}} \right)dt} } = {\int\limits_0^{\large\frac{{2{v_0}\sin\alpha }}{g}\normalsize} {\left( {0 \cdot \frac{{dx}}{{dt}} - g \cdot \frac{{dy}}{{dt}}} \right)dt} } = { - g\int\limits_0^{\large\frac{{2{v_0}\sin\alpha }}{g}\normalsize} {\left( {\frac{{dy}}{{dt}}} \right)dt} } = { - g\int\limits_0^{\large\frac{{2{v_0}\sin\alpha }}{g}\normalsize} {dy\left( t \right)} } = { - g\left[ {\left. {y\left( t \right)} \right|_{t = 0}^{\large\frac{{2{v_0}\sin\alpha }}{g}\normalsize}} \right] } = { - g\left[ {\left. {\left( {{v_0}\sin \alpha \cdot t - \frac{{g{t^2}}}{2}} \right)} \right|_{t = 0}^{\large\frac{{2{v_0}\sin\alpha }}{g}\normalsize}} \right] } = { - g\left( {\frac{{2v_0^2\,{{\sin }^2}\alpha }}{g} - \frac{{4gv_0^2\,{{\sin }^2}\alpha }}{{2{g^2}}}} \right) = 0.} \] Полученный результат объясняется тем, что гравитационное поле Земли является потенциальным, поскольку выполняется равенство \[\frac{{\partial Q}}{{\partial x}} = \frac{{\partial P}}{{\partial y}} = 0.\] Найдем потенциал этого поля. В общем виде он записывается как \[ {u\left( {x,y} \right) = \int {Pdx} + {C_1}\left( y \right) } = {\int {0dx} + {C_1}\left( y \right) } = {{C_0} + {C_1}\left( y \right).} \] Полагая \(\large\frac{{\partial u}}{{\partial y}}\normalsize = Q\left( {x,y} \right) = - g,\) находим \[\frac{d}{{dy}}{C_1}\left( y \right) = - g,\;\; \Rightarrow {C_1}\left( y \right) = - gy + {C_2}.\] Таким образом, потенциал гравитационного поля равен \[u\left( {x,y} \right) = {C_0} - gy + {C_2} = C - gy.\] где \(C\) − константа, которую можно положить равной \(0.\) В результате получаем потенциал в виде \[u\left( {x,y} \right) = - gy.\] Отсюда видно, что при перемещении тела из начальной точки \(O\left( {0,0} \right)\) до конечной точки \(A\left( {L,0} \right)\) работа равна \[W = u\left( A \right) - u\left( O \right) = 0.\]

   Пример 7

Вычислить индукцию магнитного поля в вакууме на расстоянии \(r\) от оси бесконечно длинного проводника с током \(I.\) Чтобы найти магнитное поле на расстонии \(r\) от проводника, рассмотрим круговой контур радиуса \(r,\) расположенный перпендикулярно проводнику с током (рисунок \(7\)). Поскольку поле \(\mathbf{B}\) направлено по касательной к круговому контуру в любой его точке, то скалярное произведение векторов \(\mathbf{B}\) и \(d\mathbf{r}\) есть просто \(Bdr.\) Тогда можно записать \[\oint\limits_C {\mathbf{B} \cdot d\mathbf{r}} = \oint\limits_C {Bdr} = B\oint\limits_C {dr} = 2\pi rB.\] В результате получаем \[2\pi rB = {\mu _0}I\;\;\text{или}\;\;B = \frac{{{\mu _0}I}}{{2\pi r}}.\]

   Пример 8

Оценить значение электродвижущей силы \(\varepsilon\) и электрического поля \(E,\) возникающих в кольце радиусом \(1\,\text{см}\) у пассажира самолета, при полете самолета в магнитном поле Земли со скоростью \(900\,\text{км/ч}.\) Согласно закону Фарадея \[\varepsilon = \oint\limits_C {E \cdot dr} = - \frac{{d\psi }}{{dt}}.\] Поскольку проводящее кольцо перемещается в магнитном поле Земли, возникает изменение магнитного потока \(\psi,\) проходящего через кольцо.

Предположим, что магнитное поле \(\mathbf{B}\) перпендикулярно плоскости кольца. Тогда за время \(\Delta t\) изменение потока равно \[\Delta \psi = 2rBx = 2rBv\Delta t,\] где \(x = v\Delta t,\) \(v\) − скорость самолета, \(B\) − индукция магнитного поля Земли. Из последнего выражения получаем \[\varepsilon = - \frac{{d\psi }}{{dt}} = 2rBv.\] Подставляя заданные величины \[v = 900\,\text{км/ч} = 250\,\text{м/с},\;\;r = 1\,\text{см} = 0,01\,\text{м},\;\;B = 5 \times {10^{ - 5}}\,\text{T},\] находим значение э.д.с.: \[\varepsilon = 2rBv = 2 \cdot 0,01 \cdot 5 \times {10^{ - 5}} \cdot 250 = 0,00025\,\text{В}.\] Как видно, это вполне безопасно для авиапассажиров.

Напряженность возникающего электрического поля найдем по формуле \(\varepsilon = \int\limits_C {\mathbf{E} \cdot d\mathbf{r}} .\) В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл. \[\varepsilon = \oint\limits_C {\mathbf{E} \cdot d\mathbf{r}} = \oint\limits_C {E \cdot dr \cdot \cos 0} = E\oint\limits_C {dr} = 2\pi rE.\] Следовательно, напряженность электрического поля равна \[E = \frac{\varepsilon }{{2\pi r}} = \frac{{0,00025}}{{2\pi \cdot 0,01}} = 0,004\,\text{В/м}.\]