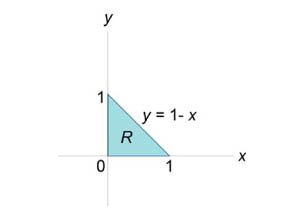Физические приложения двойных интегралов

Предположим, что плоская пластина изготовлена из неоднородного материала и занимает область \(R\) в плоскости \(Oxy.\) Пусть плотность пластины в точке \(\left( {x,y} \right)\) в области \(R\) равна \(\rho \left( {x,y} \right).\) Тогда масса пластины выражается через двойной интеграл в виде \[m = \iint\limits_R {\rho \left( {x,y} \right)dA} .\] Статический момент пластины относительно оси \(Ox\) определяется формулой \[{M_x} = \iint\limits_R {y\rho \left( {x,y} \right)dA} .\] Аналогично находится статический момент пластины относительно оси \(Oy\): \[{M_y} = \iint\limits_R {x\rho \left( {x,y} \right)dA} .\] Координаты центра масс пластины, занимающей область \(R\) в плоскости \(Oxy\) с плотностью, распределенной по закону \(\rho \left( {x,y} \right),\) описываются формулами \[ {\bar x = \frac{{{M_y}}}{m} } = {\frac{1}{m}\iint\limits_R {x\rho \left( {x,y} \right)dA} } = {\frac{{\iint\limits_R {x\rho \left( {x,y} \right)dA} }}{{\iint\limits_R {\rho \left( {x,y} \right)dA} }},} \] \[ {\bar y = \frac{{{M_x}}}{m} } = {\frac{1}{m}\iint\limits_R {y\rho \left( {x,y} \right)dA} } = {\frac{{\iint\limits_R {y\rho \left( {x,y} \right)dA} }}{{\iint\limits_R {\rho \left( {x,y} \right)dA} }}.} \] Для однородной пластины с плотностью \(\rho \left( {x,y} \right) = 1\) для всех \(\left( {x,y} \right)\) в области \(R\) центр масс определяется только формой области и называется центроидом.

Момент инерции пластины относительно оси \(Ox\) выражается формулой \[{I_x} = \iint\limits_R {{y^2}\rho \left( {x,y} \right)dA} .\] Аналогично вычисляется момент инерции пластины относительно оси \(Oy\): \[{I_y} = \iint\limits_R {{x^2}\rho \left( {x,y} \right)dA} .\] Полярный момент инерции пластины равен \[{I_0} = \iint\limits_R {\left( {{x^2} + {y^2}} \right)\rho \left( {x,y} \right)dA} .\] Предположим, что электрический заряд распределен по области \(R\) в плоскости \(Oxy\) и его плотность распределения задана функцией \({\sigma \left( {x,y} \right)}.\) Тогда полный заряд пластины \(Q\) определяется выражением \[Q = \iint\limits_R {\sigma \left( {x,y} \right)dA} .\] Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть \({f \left( {x,y} \right)}\) является непрерывной функцией в замкнутой области \(R\) в плоскости \(Oxy.\) Среднее значение \(\mu\) функции \({f \left( {x,y} \right)}\) в области \(R\) определяется формулой \[\mu = \frac{1}{S}\iint\limits_R {f\left( {x,y} \right)dA} ,\] где \(S = \iint\limits_R {dA} \) − площадь области интегрирования \(R.\)

   Пример 1

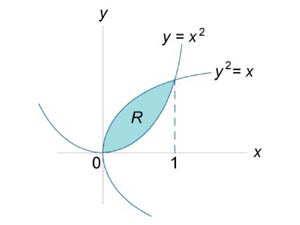
Определить координаты центра тяжести однородной пластины, образованной параболами \({y^2} = x\) и \(y = {x^2}.\) Заданная пластина имеет форму, показанную на рисунке \(1.\) Поскольку пластина однородна, то можно положить \(\rho \left( {x,y} \right) = 1.\) Тогда масса пластины равна \[ {m = \iint\limits_R {dA} } = {\int\limits_0^1 {\left[ {\int\limits_{{x^2}}^{\sqrt x } {dy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left. y \right|_{{x^2}}^{\sqrt x }} \right]dx} } = {\int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)dx} } = {\int\limits_0^1 {\left( {{x^{\large\frac{1}{2}\normalsize}} - {x^2}} \right)dx} } = {\left. {\left( {\frac{{2{x^{\large\frac{3}{2}\normalsize}}}}{3} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 } = {\frac{2}{3} - \frac{1}{3} = \frac{1}{3}.} \] Найдем теперь статические моменты относительно осей \(Ox\) и \(Oy.\) \[ {{M_x} = \iint\limits_R {ydA} } = {\int\limits_0^1 {\left[ {\int\limits_{{x^2}}^{\sqrt x } {ydy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^2}}}{2}} \right)} \right|_{{x^2}}^{\sqrt x }} \right]dx} } = {\frac{1}{2}\int\limits_0^1 {\left( {x - {x^4}} \right)dx} } = {\frac{1}{2}\left. {\left( {\frac{{{x^2}}}{2} - \frac{{{x^5}}}{5}} \right)} \right|_0^1 } = {\frac{1}{2}\left( {\frac{1}{2} - \frac{1}{5}} \right) = \frac{3}{{20}},} \] \[ {{M_y} = \iint\limits_R {xdA} } = {\int\limits_0^1 {\left[ {\int\limits_{{x^2}}^{\sqrt x } {dy} } \right]xdx} } = {\int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)xdx} } = {\int\limits_0^1 {\left( {{x^{\large\frac{3}{2}\normalsize}} - {x^3}} \right)dx} } = {\left. {\left( {\frac{{2{x^{\large\frac{5}{2}\normalsize}}}}{5} - \frac{{{x^4}}}{4}} \right)} \right|_0^1 } = {\frac{2}{5} - \frac{1}{4} = \frac{3}{{20}}.} \] Вычисляем координаты центра масс. \[ {\bar x = \frac{{{M_y}}}{m} = \frac{{\frac{3}{{20}}}}{{\frac{1}{3}}} = \frac{9}{{20}},}\;\; {\bar y = \frac{{{M_x}}}{m} = \frac{{\frac{3}{{20}}}}{{\frac{1}{3}}} = \frac{9}{{20}}.} \]

   Пример 2

Вычислить моменты инерции треугольника, ограниченного прямыми \(x + y = 1,\) \(x = 0,\) \(y = 0\) (рисунок \(2\)) и имеющего плотность \(\rho \left( {x,y} \right) = xy.\) Найдем момент инерции пластины относительно оси \(Ox:\) \[ {{I_x} = \iint\limits_R {{y^2}\rho \left( {x,y} \right)dxdy} } = {\int\limits_0^1 {\left[ {\int\limits_0^{1 - x} {{y^2}xydy} } \right]dx} } = {\int\limits_0^1 {\left[ {\int\limits_0^{1 - x} {{y^3}dy} } \right]xdx} } = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^4}}}{4}} \right)} \right|_0^{1 - x}} \right]xdx} } = {\frac{1}{4}\int\limits_0^1 {{{\left( {1 - x} \right)}^4}xdx} } = {\frac{1}{4}\int\limits_0^1 {\left( {1 - 4x + 6{x^2} - 4{x^3} + {x^4}} \right)xdx} } = {\frac{1}{4}\int\limits_0^1 {\left( {x - 4{x^2} + 6{x^3} - 4{x^4} + {x^5}} \right)dx} } = {\frac{1}{4}\left. {\left( {\frac{{{x^2}}}{2} - \frac{{4{x^3}}}{3} + \frac{{6{x^4}}}{4} - \frac{{4{x^5}}}{5} + \frac{{{x^6}}}{6}} \right)} \right|_0^1 } = {\frac{1}{4}\left( {\frac{1}{2} - \frac{4}{3} + \frac{3}{2} - \frac{4}{5} + \frac{1}{6}} \right) } = {\frac{{1}}{{120}}.} \] Аналогично вычислим момент инерции относительно оси \(Oy:\) \[ {{I_y} = \iint\limits_R {{x^2}\rho \left( {x,y} \right)dxdy} } = {\int\limits_0^1 {\left[ {\int\limits_0^{1 - x} {{x^2}xydy} } \right]dx} } = {\int\limits_0^1 {\left[ {\int\limits_0^{1 - x} {ydy} } \right]{x^3}dx} } = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^2}}}{2}} \right)} \right|_0^{1 - x}} \right]{x^3}dx} } = {\frac{1}{2}\int\limits_0^1 {{{\left( {1 - x} \right)}^2}{x^3}dx} } = {\frac{1}{2}\int\limits_0^1 {\left( {1 - 2x + {x^2}} \right){x^3}dx} } = {\frac{1}{2}\int\limits_0^1 {\left( {{x^3} - 2{x^4} + {x^5}} \right)dx} } = {\frac{1}{2}\left. {\left( {\frac{{{x^4}}}{4} - \frac{{2{x^5}}}{5} + \frac{{{x^6}}}{6}} \right)} \right|_0^1 } = {\frac{1}{2}\left( {\frac{1}{4} - \frac{2}{5} + \frac{1}{6}} \right) } = {\frac{1}{{120}}.} \]

   Пример 3

Электрический заряд распределен по площади диска \({x^2} + {y^2} = 1\) таким образом, что его поверхностная плотность равна \(\sigma \left( {x,y} \right) = 1 + {x^2} + {y^2}\;\left( {\text{Кл/м}^2} \right).\) Вычислить полный заряд диска. В полярных координатах область, занятая диском, описывается множеством \(\left\{ {\left( {r,\theta } \right)|\;0 \le r \le 1,0 \le \theta \le 2\pi } \right\}.\) Полный заряд будет равен \[ {Q = \iint\limits_R {\sigma \left( {x,y} \right)dxdy} } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^1 {\left( {1 + {r^2}{{\cos }^2}\theta + {r^2}{\sin^2}\theta } \right)rdr} } \right]d\theta } } = {\int\limits_0^{2\pi } {d\theta } \int\limits_0^1 {\left( {1 + {r^2}} \right)rdr} } = {2\pi \int\limits_0^1 {\left( {r + {r^3}} \right)dr} } = {2\pi \left. {\left( {\frac{{{r^2}}}{2} + \frac{{{r^4}}}{4}} \right)} \right|_0^1 } = {2\pi \left( {\frac{1}{2} + \frac{1}{4}} \right) } = {\frac{{3\pi }}{2}\;\left( {\text{Кл}} \right).} \]