Уравнения Лагранжа и Клеро

Дифференциальное уравнение вида \[y = x\varphi \left( {y'} \right) + \psi \left( {y'} \right),\] где \(\varphi \left( {y'} \right)\) и \(\psi \left( {y'} \right)\) − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа.

Полагая \(y' = p\) и дифференцируя по переменной \(x,\) получаем общее решение уравнения в параметрической форме: \[\left\{ \begin{array}{l} x = f\left( {p,C} \right)\\ y = f\left( {p,C} \right)\varphi \left( p \right) + \psi \left( p \right) \end{array} \right.\] при условии, что \[\varphi \left( p \right) - p \ne 0,\] где \(p\) − параметр.

Уравнение Лагранжа может также иметь особое решение, если нарушается условие \(\varphi \left( p \right) - p \ne 0.\) Особое решение определяется функцией \[y = \varphi \left( c \right)x + \psi \left( c \right),\] где \(c\) − корень уравнения \(\varphi \left( p \right) - p = 0.\) Уравнение Клеро имеет вид: \[y = xy' + \psi \left( {y'} \right),\] где \(\psi \left( {y'} \right)\) − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда \(\varphi \left( {y'} \right) = y'.\) Оно решается аналогичным образом с помощью введения параметра. Общее решение определяется выражением \[y = Cx + \psi \left( C \right),\] в котором \(C\) − произвольная постоянная.

Также как и уравнение Лагранжа, уравнение Клеро может иметь особое решение, которое выражает в параметрической форме: \[\left\{ \begin{array}{l} x = - \psi '\left( p \right)\\ y = xp + \psi \left( p \right) \end{array} \right.,\] где \(p\) − параметр.

   Пример 1

Найти все решения дифференциального уравнения \(y = 2xy' - 3{\left( {y'} \right)^2}.\) Здесь мы имеем дело с уравнением Лагранжа. Будем решать его методом введения параметра.
Обозначим \(y' = p,\) так что уравнение можно записать в форме: \[y = 2xp - 3{p^2}.\] Дифференцируя обе части, получаем: \[dy = 2xdp + 2pdx - 6pdp.\] Дифференциал \(dy\) можно заменить на \(pdx:\) \[ {pdx = 2xdp + 2pdx - 6pdp,}\;\; {\Rightarrow - pdx = 2xdp - 6pdp.} \] Разделив на \(p,\) можно записать следующее уравнение (позже мы проверим, не является ли \(p = 0\) решением исходного уравнения): \[ {- dx = \frac{{2x}}{p}dp - 6dp,}\;\; {\Rightarrow \frac{{dx}}{{dp}} + \frac{2}{p}x - 6 = 0.} \] Как видно, мы получили линейное уравнение для функции \(x\left( p \right).\) Интегрирующий множитель будет равен: \[ {u\left( p \right) = \exp \left( {\int {\frac{2}{p}dp} } \right) } = {\exp \left( {2\ln \left| p \right|} \right) } = {\exp \left( {\ln {{\left| p \right|}^2}} \right) } = {{\left| p \right|^2} } = {{p^2}.} \] Тогда общее решение линейного дифференциального уравнения имеет вид: \[ {x\left( p \right) = \frac{{\int {{p^2} \cdot 6dp} + C}}{{{p^2}}} } = {\frac{{\frac{{6{p^3}}}{3} + C}}{{{p^2}}} } = {2p + \frac{C}{{{p^2}}}.} \] Подставляя это выражение для \(x\) в уравнение Лагранжа, находим: \[ {y = 2\left( {2p + \frac{C}{{{p^2}}}} \right)p - 3{p^2} } = {4{p^2} + \frac{{2C}}{p} - 3{p^2} } = {{p^2} + \frac{{2C}}{p}.} \] Таким образом, общее решение в параметрической форме определяется системой уравнений: \[\left\{ \begin{array}{l} x\left( p \right) = 2p + \frac{C}{{{p^2}}}\\ y\left( p \right) = {p^2} + \frac{{2C}}{p} \end{array} \right..\] Кроме общего решения, уравнение Лагранжа может иметь еще особое решение. Решая алгебраическое уравнение \(\varphi \left( p \right) - p = 0,\) находим корень: \[2p - p = 0,\;\; \Rightarrow p = 0.\] Следовательно, особое решение представляется в виде следующей линейной функции: \[y = \varphi \left( 0 \right)x + \psi \left( 0 \right) = 0 \cdot x + 0 = 0.\]

   Пример 2

Найти общее и особое решения уравнения \(2y - 4xy' - \ln y' = 0.\) Здесь мы снова имеем дело с уравнением Лагранжа. Полагая \(y' = p,\) можно записать: \[2y = 4xp + \ln p.\] Дифференцируем обе части уравнения: \[2dy = 4xdp + 4pdx + \frac{{dp}}{p}.\] Поскольку \(dy = pdx,\) то получаем: \[ {2pdx = 4xdp + 4pdx + \frac{{dp}}{p},}\;\; {\Rightarrow - 2pdx = 4xdp + \frac{{dp}}{p},}\;\; {\Rightarrow - 2p\frac{{dx}}{{dp}} = 4x + \frac{1}{p},}\;\; {\Rightarrow \frac{{dx}}{{dp}} + \frac{2}{p}x = - \frac{1}{{2{p^2}}}.} \] При делении на \(p\) мы потеряли корень \(p = 0,\) который соответствует решению \(y = 0.\)

Таким образом, мы получаем линейное дифференциальное уравнение для функции \(x\left( p \right).\) Решим его с помощью интегрирующего множителя: \[ {u\left( p \right) = \exp \left( {\int {\frac{2}{p}dp} } \right) } = {\exp \left( {2\ln \left| p \right|} \right) } = {\exp \left( {\ln {{\left| p \right|}^2}} \right) } = {{\left| p \right|^2} } = {{p^2}.} \] Функция \(x\left( p \right)\) определяется формулой \[ {x\left( p \right) = \frac{{\int {{p^2} \cdot \left( { - \frac{1}{{2{p^2}}}} \right)dp} + C}}{{{p^2}}} } = {\frac{{ - \frac{p}{2} + C}}{{{p^2}}} } = { - \frac{1}{{2p}} + \frac{C}{{{p^2}}}.} \] Подставляя это в исходное уравнение, находим параметрическое выражение для \(y:\) \[ {2y = 4xp + \ln p,}\;\; {\Rightarrow 2y = 4p\left( { - \frac{1}{{2p}} + \frac{C}{{{p^2}}}} \right) + \ln p,}\;\; {\Rightarrow 2y = - 2 + \frac{{4C}}{p} + \ln p,}\;\; {\Rightarrow y = \frac{{2C}}{p} - 1 + \frac{{\ln p}}{2}.} \] Следовательно, общее решение уравнения в параметрической форме записывается в виде: \[\left\{ \begin{array}{l} x\left( p \right) = \frac{C}{{{p^2}}} - \frac{1}{{2p}}\\ y\left( p \right) = \frac{{2C}}{p} - 1 + \frac{{\ln p}}{2} \end{array} \right..\] Чтобы найти особое решение, решим следующее алгебраическое уравнение: \[ {\varphi \left( p \right) - p = 0,}\;\; {\Rightarrow 2p - p = 0,}\;\; {\Rightarrow p = 0.} \] Отсюда следует, что \(y = C.\) Путем прямой подстановки можно убедиться, что постоянная \(C\) должна быть равна нулю.

Итак, заданное дифференциальное уравнение имеет особое решение \(y = 0.\) Мы уже встречались с этим корнем выше при делении уравнения на \(p.\)

   Пример 3

Найти общее и особое решения дифференциального уравнения \(y = xy' + {\left( {y'} \right)^2}.\) Здесь мы имеем дело с уравнением Клеро. Полагая \(y' = p,\) его можно записать в виде \[y = xp + {p^2}.\] Продифференцировав по переменной \(x,\) находим: \[dy = xdp + pdx + 2pdp.\] Заменим \(dy\) на \(pdx:\) \[\require{cancel} {\cancel{pdx} = xdp + \cancel{pdx} + 2pdp,}\;\; {\Rightarrow dp\left( {x + 2p} \right) = 0.} \] Приравнивая первый множитель к нулю, получаем: \[dp = 0,\;\; \Rightarrow p = C.\] Теперь подставим это во второе уравнение: \[y = Cx + {C^2}.\] В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых.

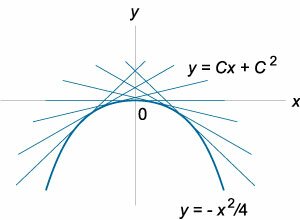
Приравнивая нулю второй сомножитель, находим еще одно решение: \[x + 2p = 0,\;\; \Rightarrow x = - 2p.\] Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как \[\left\{ \begin{array}{l} x = - 2p\\ y = xp + {p^2} \end{array} \right..\] Исключая \(p\) из системы, получаем следующее уравнение интегральной кривой: \[ {p = - \frac{x}{2},}\;\; {\Rightarrow y = x\left( { - \frac{x}{2}} \right) + {\left( { - \frac{x}{2}} \right)^2} } = { - \frac{{{x^2}}}{2} + \frac{{{x^2}}}{4} } = { - \frac{{{x^2}}}{4}.} \] С геометрической точки зрения, парабола \(y = - \large\frac{{{x^2}}}{4}\normalsize\) является огибающей семейства прямых, определяемых общим решением (Рисунок \(1\)).

   Пример 4

Найти общее и особое решения дифференциального уравнения \(y = xy' + \sqrt {{{\left( {y'} \right)}^2} + 1} .\) Как видно, это уравнение является уравнением Клеро. Введем параметр \(y' = p:\) \[y = xp + \sqrt {{p^2} + 1} .\] Дифференцируя обе части уравнения по переменной \(x,\) получаем: \[dy = xdp + pdx + \frac{{pdp}}{{\sqrt {{p^2} + 1} }}.\] Поскольку \(dy = pdx,\) то можно записать: \[ {\cancel{pdx} = xdp + \cancel{pdx} + \frac{{pdp}}{{\sqrt {{p^2} + 1} }},}\;\; {\Rightarrow \left( {x + \frac{p}{{\sqrt {{p^2} + 1} }}} \right)dp = 0.} \] Рассмотрим случай \(dp = 0.\) Тогда \(p = C.\) Подставляя это в уравнение, находим общее решение: \[y = Cx + \sqrt {{C^2} + 1} .\] Графически это решение соответствует однопараметрическому семейству прямых линий.

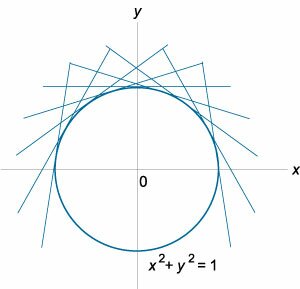
Второй случай описывается уравнением \(x = - \large\frac{p}{{\sqrt {{p^2} + 1} }}\normalsize.\) Найдем соответствующее параметрическое выражение для \(y:\) \[ {y = xp + \sqrt {{p^2} + 1} } = { - \frac{{p^2}}{{\sqrt {{p^2} + 1} }} + \sqrt {{p^2} + 1} } = {\frac{{ - \cancel{p^2} + \cancel{p^2} + 1}}{{\sqrt {{p^2} + 1} }} } = {\frac{1}{{\sqrt {{p^2} + 1} }}.} \] Параметр \(p\) можно исключить из формул для \(x\) и \(y.\) Возводя последние уравнения в квадрат и складывая их, получаем: \[ {{x^2} + {y^2} } = {{\left( { - \frac{p}{{\sqrt {{p^2} + 1} }}} \right)^2} + {\left( {\frac{1}{{\sqrt {{p^2} + 1} }}} \right)^2} } = {\frac{\cancel{{p^2} + 1}}{\cancel{{p^2} + 1}} = 1.} \] Полученное выражение является уравнением окружности радиусом \(1,\) расположенным в начале координат. Таким образом, особое решение представляется единичной окружностью в плоскости \(xy,\) которая является огибающей для семейства прямых линий (Рисунок \(2\)).