Тройные интегралы в декартовых координатах

Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.

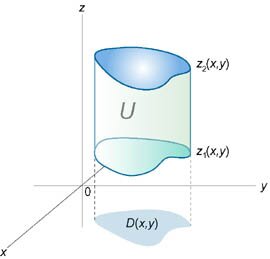
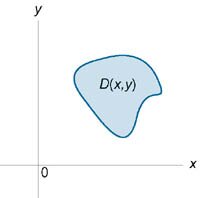
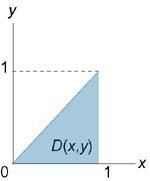
Рассмотрим случай, когда область интегрирования \(U\) является элементарной относительно оси \(Oz\), т.е. любая прямая, параллельная оси \(Oz,\) пересекает границу области \(U\) не более, чем в двух точках. Пусть область \(U\) ограничена снизу поверхностью \(z = {z_1}\left( {x,y} \right),\) а сверху − поверхностью \(z = {z_2}\left( {x,y} \right)\) (рисунок \(1\)). Проекцией тела \(U\) на плоскость \(Oxy\) является область \(D\) (рисунок \(2\)). Будем предполагать, что функции \({z_1}\left( {x,y} \right)\) и \({z_2}\left( {x,y} \right)\) непрерывны в области \(D.\) Тогда для любой непрерывной в области \(U\) функции \(f\left( {x,y,z} \right)\) можно записать соотношение \[ {\iiint\limits_U {f\left( {x,y,z} \right)dV} } = {\iint\limits_D {\left[ {\int\limits_{{z_1}\left( {x,y} \right)}^{{z_2}\left( {x,y} \right)} {f\left( {x,y,z} \right)dz} } \right]dA} .} \] Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной \(z,\) а затем − двойной интеграл в области \(D\) по переменным \(x\) и \(y.\)

Если область \(D\left( {x,y} \right)\) является областью типа \(I\) (смотрите Повторные интегралы), т.е. ограничена линиями \[ {x = a,\;\;x = b,}\;\; {y = {f_1}\left( x \right),}\;\; {y = {f_2}\left( x \right),} \] где \({f_1}\left( x \right),\) \({f_2}\left( x \right)\) − непрерывные функции в интервале \(\left[ {a,b} \right]\) и \({f_1}\left( x \right) \le {f_2}\left( x \right),\) то, записывая двойной интеграл в виде повторного, получаем \[ {\iiint\limits_U {f\left( {x,y,z} \right)dV} } = {\int\limits_a^b {dx} \int\limits_{{f_1}\left( x \right)}^{{f_2}\left( x \right)} {dy} \int\limits_{{z_1}\left( {x,y} \right)}^{{z_2}\left( {x,y} \right)} {f\left( {x,y,z} \right)dz}. \qquad \left( 1 \right) } \] В другом случае, когда область \(D\left( {x,y} \right)\) относится к типу \(II\) (является элементарной относительно оси \(Ox\)) и ограничена линиями \[ {y = c,\;\;y = d,}\;\; {x = {\varphi _1}\left( y \right),}\;\; {x = {\varphi _2}\left( y \right),} \] где \({\varphi _1}\left( y \right),\) \({\varphi _2}\left( y \right),\) − непрерывные на отрезке \(\left[ {c,d} \right]\) функции, причем \({\varphi _1}\left( y \right) \le {\varphi _2}\left( y \right),\) тройной интеграл представляется в виде \[ {\iiint\limits_U {f\left( {x,y,z} \right)dV} } = {\int\limits_c^d {dy} \int\limits_{{\varphi _1}\left( y \right)}^{{\varphi _2}\left( y \right)} {dx} \int\limits_{{z_1}\left( {x,y} \right)}^{{z_2}\left( {x,y} \right)} {f\left( {x,y,z} \right)dz} .} {\qquad \left( 2 \right) } \] Формулы \(\left( 1 \right)\) и \(\left( 2 \right)\) называются формулами сведения тройного интеграла к повторному.

В частном случае, когда область интегрирования \(U\) представляет собой прямоугольный параллелепипед \(\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right],\) тройной интеграл вычисляется по формуле \[ {\iiint\limits_U {f\left( {x,y,z} \right)dxdydz} } = {\int\limits_a^b {dx} \int\limits_c^d {dy} \int\limits_p^q {f\left( {x,y,z} \right)dz} .} \] Если исходная область интегрирования \(U,\) более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным.

   Пример 1

Вычислить интеграл \[\int\limits_0^2 {\int\limits_0^z {\int\limits_0^y {xyzdxdydz} } } .\] Найдем последовательно все три интеграла: \[ {I = \int\limits_0^2 {\int\limits_0^z {\int\limits_0^y {xyzdxdydz} } } } = {\int\limits_0^2 {dz} \int\limits_0^z {dy} \int\limits_0^y {xyzdz} } = {\int\limits_0^2 {dz} \int\limits_0^z {dy} \left[ {\left. {\left( {\frac{{{x^2}yz}}{2}} \right)} \right|_{x = 0}^{x = y}} \right] } = {\int\limits_0^2 {dz} \int\limits_0^z {\frac{{{y^3}z}}{2}dy} } = {\frac{1}{2}\int\limits_0^2 {dz} \int\limits_0^z {{y^3}zdy} } = {\frac{1}{2}\int\limits_0^2 {dz} \left[ {\left. {\left( {\frac{{{y^4}z}}{4}} \right)} \right|_{y = 0}^{y = z}} \right] } = {\frac{1}{2}\int\limits_0^2 {\frac{{{z^5}}}{4}dz} } = {\frac{1}{8}\int\limits_0^2 {{z^5}dz} } = {\frac{1}{8}\left. {\left( {\frac{{{z^6}}}{6}} \right)} \right|_0^2 } = {\frac{{64}}{{48}} = \frac{4}{3}.} \]

   Пример 2

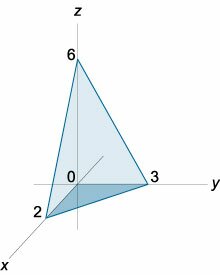
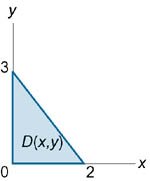
Вычислить интеграл \[\iiint\limits_U {\left( {1 - x} \right)dxdydz} ,\] где область \(U\) расположена в первом октанте ниже плоскости \(3x + 2y + z = 6.\) Записывая уравнение плоскости \(3x + 2y + z = 6\) в отрезках: \[ {3x + 2y + z = 6,}\;\; {\Rightarrow \frac{x}{2} + \frac{y}{3} + \frac{z}{6} = 1,} \] изобразим область интегрирования \(U\) (рисунок \(3\)). Пределы интегрирования по \(z\) изменяются от \(z = 0\) до \(z = 6 - 3x - 2y.\) Рассматривая проекцию \(D\) в плоскости \(Oxy,\) находим, что переменная \(y\) изменяется от \(y = 0\) до \(y = 3 - \large\frac{3}{2}\normalsize x\) (рисунок \(4\)). При этом переменная \(x\) "пробегает" от \(0\) до \(2.\)

Итак, тройной интеграл выражается через повторный в виде \[ {I = \iiint\limits_U {\left( {1 - x} \right)dxdydz} } = {\int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {dy} \int\limits_0^{6 - 3x - 2y} {\left( {1 - x} \right)dz} .} \] Вычисляем последовательно все три интеграла и находим ответ: \[ {I = \int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {dy} \int\limits_0^{6 - 3x - 2y} {\left( {1 - x} \right)dz} } = {\int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {dy} \left[ {\left. {\left( {z - zx} \right)} \right|_{z = 0}^{z = 6 - 3x - 2y}} \right] } = {\int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {\left[ {6 - 3x - 2y - \left( {6 - 3x - 2y} \right)x} \right]dy} } = {\int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {\left( {6 - 3x - 2y - 6x + 3{x^2} + 2xy} \right)dy} } = {\int\limits_0^2 {dx} \int\limits_0^{3 - \frac{3}{2}x} {\left( {6 - 9x - 2y + 3{x^2} + 2xy} \right)dy} } = {\int\limits_0^2 {dx} \left[ {\left. {\left( {6y - 9xy - \frac{{2{y^2}}}{2} + 3{x^2}y + \frac{{2x{y^2}}}{2}} \right)} \right|_{y = 0}^{y = 3 - \frac{3}{2}x}} \right] } = {\int\limits_0^2 {\left( {9 - 18x + \frac{{45}}{4}{x^2} - \frac{9}{4}{x^3}} \right)dx} } = {\left. {\left( {9x - \frac{{18}}{2}{x^2} + \frac{{45}}{{12}}{x^3} - \frac{9}{{16}}{x^4}} \right)} \right|_0^2 } = {18 - 36 + 30 - 9 = 3.} \]

   Пример 3

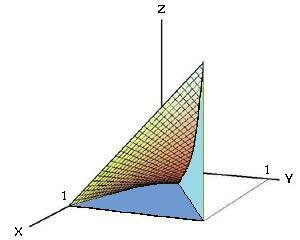
Вычислить тройной интеграл \[\iiint\limits_U {x{y^2}{z^3}dxdydz} ,\] где область \(U\) (рисунок \(5\)) ограничена поверхностями \[ {z = xy,}\;\; {y = x,}\;\; {x = 0,}\;\; {x = 1,}\;\; {z = 0.} \] Проекция области \(U\) на плоскость \(Oxy\) имеет вид, показанный на рисунке \(6.\) Учитывая это, найдем соответствующие повторные интегралы: \[ {I = \iiint\limits_U {x{y^2}{z^3}dxdydz} } = {\int\limits_0^1 {dx} \int\limits_0^x {dy} \int\limits_0^{xy} {x{y^2}{z^3}dz} } = {\int\limits_0^1 {dx} \int\limits_0^x {dy} \left[ {\left. {\left( {\frac{{x{y^2}{z^4}}}{4}} \right)} \right|_{z = 0}^{z = xy}} \right] } = {\int\limits_0^1 {dx} \int\limits_0^x {\left( {x{y^2}\frac{{{x^4}{y^4}}}{4}} \right)dy} } = {\frac{1}{4}\int\limits_0^1 {dx} \int\limits_0^x {{x^5}{y^6}dy} } = {\frac{1}{4}\int\limits_0^1 {dx} \left[ {\left. {\left( {\frac{{{x^5}{y^7}}}{7}} \right)} \right|_{y = 0}^{y = x}} \right] } = {\frac{1}{4}\int\limits_0^1 {\left( {{x^5}\frac{{{x^7}}}{7}} \right)dx} } = {\frac{1}{{28}}\int\limits_0^1 {{x^{12}}dx} } = {\frac{1}{{28}}\left. {\left( {\frac{{{x^{13}}}}{{13}}} \right)} \right|_0^1 } = {\frac{1}{{28}} \cdot \frac{1}{{13}} = \frac{1}{{364}}.} \]

   Пример 4

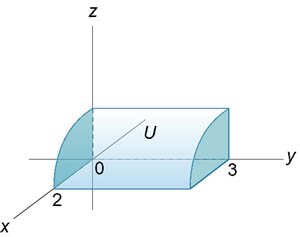
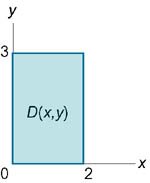
Выразить тройной интеграл \(\iiint\limits_U {dxdydz} \) через повторные интегралы шестью различными способами. Область \(U\) расположена в первом октанте и ограничена цилиндром \({x^2} + {z^2} = 4\) и плоскостью \(y = 3\) (рисунок \(7\)). Найти значение интеграла. Если порядок интегрирования имеет вид \(z-y-x,\) то повторный интеграл выглядит как \[ {{I_1} = \iiint\limits_U {dxdydz} } = {\int\limits_0^2 {dx} \int\limits_0^3 {dy} \int\limits_0^{\sqrt {4 - {x^2}} } {dz} .} \] Аналогично записывается повторный интеграл для последовательности интегрирования \(z-x-y:\) \[{I_2} = \int\limits_0^3 {dy} \int\limits_0^2 {dx} \int\limits_0^{\sqrt {4 - {x^2}} } {dz} .\] Теперь рассмотрим случай \(x-y-z,\) т.е. когда первый внутренний интеграл берется по переменной \(x.\) Тогда \[{I_3} = \int\limits_0^2 {dz} \int\limits_0^3 {dy} \int\limits_0^{\sqrt {4 - {z^2}} } {dx} .\] Поскольку проекция тела на плоскость \(Oyz\) представляет собой прямоугольник (рисунок \(8\)), то меняя порядок интегрирования по \(y\) и \(z,\) получаем \[{I_4} = \int\limits_0^3 {dy\int\limits_0^2 {dz\int\limits_0^{\sqrt {4 - {z^2}} } {dx} } } .\] Наконец, повторный интеграл при интегрировании в порядке \(y-x-z\) (начиная с внутреннего интеграла) имеет вид: \[{I_5} = \int\limits_0^2 {dz\int\limits_0^{\sqrt {4 - {z^2}} } {dx\int\limits_0^3 {dy} } } .\] Последний шестой вариант записывается в виде: \[{I_6} = \int\limits_0^2 {dx\int\limits_0^{\sqrt {4 - {x^2}} } {dz\int\limits_0^3 {dy} } } .\] Мы можем использовать любой из шести повторных интегралов, чтобы вычислить значение тройного интеграла. Например, используя последний интеграл, получаем: \[ {I = {I_6} = \int\limits_0^2 {dx\int\limits_0^{\sqrt {4 - {x^2}} } {dz\int\limits_0^3 {dy} } } } = {\int\limits_0^2 {dx\int\limits_0^{\sqrt {4 - {x^2}} } {dz \cdot \left[ {\left. y \right|_0^3} \right]} } } = {3\int\limits_0^2 {dx\int\limits_0^{\sqrt {4 - {x^2}} } {dz} } } = {3\int\limits_0^2 {dx\left[ {\left. z \right|_0^{\sqrt {4 - {x^2}} }} \right]} } = {3\int\limits_0^2 {\sqrt {4 - {x^2}} dx} .} \] Сделаем замену: \[x = 2\sin t,\;\; \Rightarrow dx = 2\cos tdt,\] \[x = 0,\;\; \Rightarrow t = 0,\] \[x = 2,\;\; \Rightarrow \sin t = 1,\;\; \Rightarrow t = \frac{\pi }{2}.\] Находим окончательный ответ: \[ {I = 3\int\limits_0^2 {\sqrt {4 - {x^2}} dx} } = {3\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sqrt {4 - {{\left( {2\sin t} \right)}^2}} \cdot 2\cos tdt} } = {12\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sqrt {1 - {{\sin }^2}t} \cos tdt} } = {12\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}tdt} } = {12\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{1 + \cos 2t}}{2}dt} } = {6\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize} } = {6 \cdot \frac{\pi }{2} = 3\pi .} \] Нетрудно проверить, что данное значение в точности равно \(\large\frac{1}{4}\normalsize\) объема цилиндра, по которому проводилось интегрирование.