Точки разрыва функции

Математический Анализ

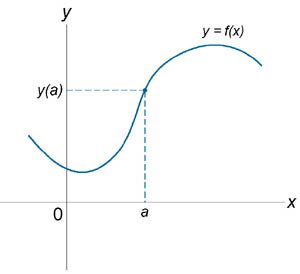
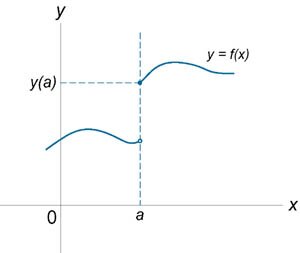
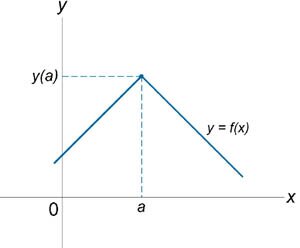
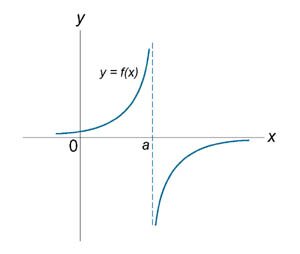
Если функция \(f\left( x \right)\) не является непрерывной в точке \(x = a\), то говорят, что \(f\left( x \right)\) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при \(x =a\), а две имеют разрыв.


Непрерывна при \(x =a\).		Имеет разрыв при \(x =a\).

Непрерывна при \(x =a\).		Имеет разрыв при \(x =a\).
Рисунок 1.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция \(f\left( x \right)\) имеет точку разрыва первого рода при \(x = a\), если в это точке

Существуют левосторонний предел \(\lim\limits_{x \to a - 0} f\left( x \right)\) и правосторонний предел \(\lim\limits_{x \to a + 0} f\left( x \right)\);
Эти односторонние пределы конечны.

При этом возможно следующие два случая:

Левосторонний предел и правосторонний предел равны друг другу: \[\lim\limits_{x \to a - 0} f\left( x \right) = \lim\limits_{x \to a + 0} f\left( x \right).\] Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу: \[\lim\limits_{x \to a - 0} f\left( x \right) \ne \lim\limits_{x \to a + 0} f\left( x \right).\] Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов \(\left| \lim\limits_{x \to a - 0} f\left( x \right) - \lim\limits_{x \to a + 0} f\left( x \right) \right|\) называется скачком функции.

Функция \(f\left( x \right)\) имеет точку разрыва второго рода при \(x =a\), если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Исследовать функцию \(f\left( x \right) = {3^{\large\frac{x}{{1 - {x^2}}}\normalsize}}\) на непрерывность.

Решение.

Данная функция не определена в точках \(x = -1\) и \(x = 1\). Следовательно, функция имеет разрывы в точках \(x = \pm 1\). Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. \[ {\lim\limits_{x \to - 1 - 0} {3^{\large\frac{x}{{1 - {x^2}}}\normalsize}} = {3^{\large\frac{{ - 1}}{{ - 0}}\normalsize}} = {3^\infty } = \infty ,\;\;} {\lim\limits_{x \to - 1 + 0} {3^{\large\frac{x}{{1 - {x^2}}}\normalsize}} = {3^{\large\frac{{ - 1}}{{ + 0}}\normalsize}} = {3^{ - \infty }} = \frac{1}{{{3^\infty }}} = 0.} \] Поскольку левосторонний предел при \(x = -1\) равен бесконечности, то данная точка является точкой разрыва второго рода. \[ {\lim\limits_{x \to 1 - 0} {3^{\large\frac{x}{{1 - {x^2}}}\normalsize}} = {3^{\large\frac{{ 1}}{{ +0}}\normalsize}} = {3^\infty } = \infty ,\;\;} {\lim\limits_{x \to 1 + 0} {3^{\large\frac{x}{{1 - {x^2}}}\normalsize}} = {3^{\large\frac{{ 1}}{{ -0}}\normalsize}} = {3^{ - \infty }} = \frac{1}{{{3^\infty }}} = 0.} \] Аналогично, левосторонний предел в точке \(x = 1\) равен бесконечности. Эта точка также является точкой разрыва второго рода.

Показать, что функция \(f\left( x \right) = \large\frac{{\sin x}}{x}\normalsize\) имеет устранимый разрыв в точке \(x = 0\).

Решение.

Очевидно, данная функция не определена при \(x = 0\). Поскольку \(\sin x\) является непрерывной функцией для всех \(x\), то искомая функция \(f\left( x \right) = \large\frac{{\sin x}}{x}\normalsize\) также непрерывна при всех \(x\) за исключением точки \(x = 0\).
Так как \(\lim\limits_{x \to 0} \large\frac{{\sin x}}{x}\normalsize = 1\), то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию \[ {f_1}\left( x \right) = \begin{cases} \large\frac {\sin x}{x}\normalsize, & x \ne 0 \\ 1, &x = 0 \end{cases} ,\] которая будет непрерывной при любом действительном \(x\).

Найти точки разрыва функции \( f\left( x \right) = \begin{cases} 1 - {x^2}, & x < 0 \\ x +2, &x \ge 0 \end{cases} ,\,\) если они существуют.

Решение.

Данная функция существует при всех значениях \(x\), однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки \(x = 0\), где ее аналитическое выражение изменяется.

Вычислим односторонние пределы при \(x = 0\). \[ {\lim\limits_{x \to 0 - 0} f\left( x \right) = \lim\limits_{x \to 0 - 0} \left( {1 - {x^2}} \right) = 1,}\;\;\; {\lim\limits_{x \to 0 + 0} f\left( x \right) = \lim\limits_{x \to 0 - 0} \left( {x + 2} \right) = 2.} \] Следовательно, функция имеет точку разрыва первого рода при \(x = 0\). Скачок функции в этой точке равен \[ {\Delta y = \lim\limits_{x \to 0 + 0} f\left( x \right) - \lim\limits_{x \to 0 - 0} f\left( x \right) } {= 2 - 1 = 1.} \] При всех других значениях \(x\)функция является непрерывной, поскольку обе составляющие функции слева и справа от точки \(x = 0\) представляют собой элементарные функции без точек разрыва.

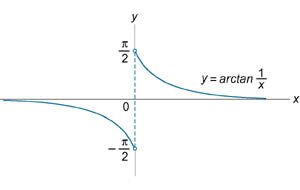
Найти точки разрыва функции \(f\left( x \right) = \arctan \large\frac{1}{x}\normalsize\), если они существуют.

Решение.

Данная элементарная функция определена для всех \(x\), исключая точку \(x = 0\), где она имеет разрыв. Найдем односторонние пределы в этой точке. \[ {\lim\limits_{x \to 0 - 0} \arctan \frac{1}{x} = \arctan \left( { - \infty } \right) = - \frac{\pi }{2},}\;\; {\lim\limits_{x \to 0 + 0} \arctan \frac{1}{x} = \arctan \left( { + \infty } \right) = \frac{\pi }{2}.} \] Видно, что в точке \(x = 0\) существует разрыв первого рода (рисунок 2). Скачок функции равен \(\pi\).


Рис.2		Рис.3

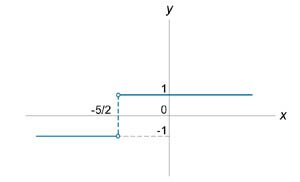
Найти точки разрыва функции \(f\left( x \right) = \large\frac{{\left| {2x + 5} \right|}}{{2x + 5}}\normalsize\), если таковые существуют.

Решение.

Функция определена и непрерывна при всех \(x\), за исключением точки \(x = - \large\frac{5}{2}\normalsize\), где существует разрыв. Исследуем точку разрыва. \[ {\lim\limits_{x \to - \frac{5}{2} - 0} \frac{{\left| {2x + 5} \right|}}{{2x + 5}} } = {\lim\limits_{x \to - \frac{5}{2} - 0} \frac{{ - \left( {2x + 5} \right)}}{{2x + 5}} = - 1,}\;\; {\text{если}\;\;x < - \frac{5}{2};} \] \[ {\lim\limits_{x \to - \frac{5}{2} + 0} \frac{{\left| {2x + 5} \right|}}{{2x + 5}} } = {\lim\limits_{x \to - \frac{5}{2} + 0} \frac{{ \left( {2x + 5} \right)}}{{2x + 5}} = 1,}\;\; {\text{если}\;\;x \ge - \frac{5}{2}.} \] Так как значения односторонних пределов конечны, то, следовательно, в точке \(x = - \large\frac{5}{2}\normalsize\) существует разрыв первого рода. График функции схематически показан на рисунке \(3\).