Точки перегиба

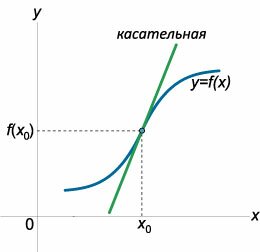
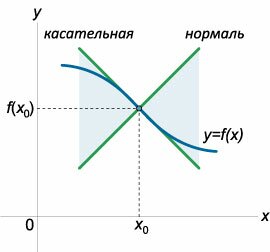
Рассмотрим функцию \(y = f\left( x \right),\) которая является непрерывной в точке \({x_0}.\) Функция \(f\left( x \right)\) может иметь в этой точке конечную или бесконечную производную \(f'\left( {{x_0}} \right).\) Если при переходе через \({x_0}\) функция меняет направление выпуклости, т.е. существует число \(\delta > 0,\) такое, что на одном из интервалов \(\left( {{x_0} - \delta ,{x_0}} \right)\) или \(\left( {{x_0},{x_0} + \delta } \right)\) функция является выпуклой вверх, а на другом − выпуклой вниз, то \({x_0}\) называется точкой перегиба функции \(y = f\left( x \right).\)

Геометрический смысл точки перегиба состоит в том, что график функции \(f\left( x \right)\) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются (рисунок \(1\)).

Другое интересное свойство точки перегиба состоит в том, что график функции \(f\left( x \right)\) в окрестности точки перегиба \({x_0}\) расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок \(2\)). Если \({x_0}\) − точка перегиба функции \(f\left( x \right)\) и данная функция имеет вторую производную в некоторой окрестности точки \({x_0},\) причем в точке \({x_0}\) она непрерывна, то \[f''\left( {{x_0}} \right) = 0.\] Доказательство.
Предположим, что в точке перегиба \({x_0}\) вторая производная не равна нулю: \(f''\left( {{x_0}} \right) \ne 0.\) Поскольку она непрерывна при \({x_0},\) то существует \(\delta\)-окрестность точки \({x_0},\) в которой вторая производная сохраняет свой знак, т.е. \[f''\left( {{x_0}} \right) < 0\;\;\text{или}\;\;f''\left( {{x_0}} \right) < 0\;\forall \;x \in \left( {{x_0} - \delta ,{x_0} + \delta } \right).\] В таком случае функция будет либо строго выпукла вверх (при \(f''\left( x \right) < 0\)), либо строго выпукла вниз (при \(f''\left( x \right) > 0\)). Но тогда точка \({x_0}\) не является точкой перегиба. Следовательно, предположение неверно и вторая производная в точке перегиба должна быть равна нулю. Если функция \(f\left( x \right)\) непрерывна и дифференцируема в точке \({x_0},\) имеет вторую производную \(f''\left( {{x_0}} \right)\) в некоторой проколотой \(\delta\)-окрестности точки \({x_0}\) и если вторая производная меняет знак при переходе через точку \({x_0},\) то \({x_0}\) является точкой перегиба функции \(f\left( x \right).\)

Доказательство.
Пусть, например, вторая производная \(f''\left( x \right)\) при переходе через точку \({x_0}\) меняет знак с плюса на минус. Следовательно, в левой \(\delta\)-окрестности \(\left( {{x_0} - \delta ,{x_0}} \right)\) выполняется неравенство \(f''\left( x \right) > 0,\) а в правой \(\delta\)-окрестности \(\left( {{x_0},{x_0} + \delta } \right)\) справедливо неравенство \(f''\left( x \right) < 0.\)

В таком случае, согласно достаточным условиям выпуклости, функция \(f\left( x \right)\) выпукла вниз в левой \(\delta\)-окрестности точки \({x_0}\) и выпукла вверх в правой \(\delta\)-окрестности.

Следовательно, в точке \({x_0}\) функция меняет направление выпуклости, т.е. c является, по определению, точкой перегиба. Пусть \(f''\left( {{x_0}} \right) = 0,\) \(f'''\left( {{x_0}} \right) \ne 0.\) Тогда точка \({x_0}\) является точкой перегиба функции \(f\left( x \right).\)

Доказательство.
Поскольку \(f'''\left( {{x_0}} \right) \ne 0,\) то вторая производная в точке \({x_0}\) либо строго возрастает (если \(f'''\left( {{x_0}} \right) > 0\)), либо строго убывает (если \(f'''\left( {{x_0}} \right) < 0\)). Так как \(f''\left( {{x_0}} \right) = 0,\) то вторая производная при некотором \(\delta > 0\) имеет разные знаки в левой и правой \(\delta\)-окрестности точки \({x_0}.\) Отсюда, на основании предыдущей теоремы, следует что \({x_0}\) − точка перегиба функции \(f\left( x \right).\)

   Пример 1

Выяснить, является ли точка \(x = 0\) точкой перегиба функции \(f\left( x \right) = \sin x.\) Воспользуемся вторым достаточным признаком существования точки перегиба. Найдем производные синуса до третьего порядка включительно: \[ {f'\left( x \right) = {\left( {\sin x} \right)^\prime } = \cos x,}\;\; {f''\left( x \right) = {\left( {\cos x} \right)^\prime } = - \sin x,}\;\; {f'''\left( x \right) = {\left( { - \sin x} \right)^\prime } = - \cos x.} \] В точке \(x = 0\) вторая и третья производные имеют следующие значения: \[ {f''\left( 0 \right) = - \sin 0 = 0,}\;\; {f'''\left( 0 \right) = - \cos 0 = - 1.} \] Таким образом, имеем \(f''\left( {{x_0}} \right) = 0,\) \(f'''\left( {{x_0}} \right) \ne 0.\) Следовательно, по второму достаточному признаку точка \(x = 0\) является точкой перегиба.

   Пример 2

Найти точки перегиба функции \[f\left( x \right) = {x^4} - 12{x^3} + 48{x^2} + 12x + 1.\] Находим производные: \[ {f'\left( x \right) } = {{\left( {{x^4} - 12{x^3} + 48{x^2} + 12x + 1} \right)^\prime } } = {4{x^3} - 36{x^2} + 96x + 12 } = {4\left( {{x^3} - 9{x^2} + 24x + 3} \right);} \] \[ {f''\left( x \right) } = {{\left( {4\left( {{x^3} - 9{x^2} + 24x + 3} \right)} \right)^\prime } } = {4\left( {3{x^2} - 18x + 24} \right) } = {12\left( {{x^2} - 6x + 8} \right).} \] Вычисляем корни второй производной: \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow 12\left( {{x^2} - 6x + 8} \right) = 0,}\;\; {\Rightarrow {x^2} - 6x + 8 = 0,}\;\; {\Rightarrow {x_1} = 2,\;{x_2} = 4.} \] В данном случае удобно использовать второй достаточный признак существования точки перегиба. Третья производная записывается в виде \[ {f'''\left( x \right) } = {{\left( {12\left( {{x^2} - 6x + 8} \right)} \right)^\prime } } = {12\left( {2x - 6} \right) = 24\left( {x - 3} \right).} \] Отсюда сразу видно, что в точках \({x_1} = 2,\) \({x_2} = 4\) третья производная не равна нулю. Следовательно, эти точки будут являться точками перегиба.

   Пример 3

Найти точки перегиба функции \(f\left( x \right) = {x^2}\ln x.\) Находим вторую производную: \[ {f'\left( x \right) = {\left( {{x^2}\ln x} \right)^\prime } } = {{\left( {{x^2}} \right)^\prime }\ln x + {x^2}{\left( {\ln x} \right)^\prime } } = {2x\ln x + {x^2} \cdot \frac{1}{x} } = {2x\ln x + x = x\left( {2\ln x + 1} \right);} \] \[ {f''\left( x \right) = {\left[ {x\left( {2\ln x + 1} \right)} \right]^\prime } } = {x'\left( {2\ln x + 1} \right) + x{\left( {2\ln x + 1} \right)^\prime } } = {2\ln x + 1 + x \cdot \frac{2}{x} = 2\ln x + 3.} \] Решаем уравнение \(f''\left( x \right) = 0:\) \[ {\Rightarrow 2\ln x + 3,}\;\; {\Rightarrow \ln x = - \frac{3}{2},}\;\; {\Rightarrow x = {e^{ - \large\frac{3}{2}\normalsize}} = \frac{1}{{\sqrt {{e^3}} }}.} \] Вторая производная представляет собой монотонно возрастающую функцию. Поэтому в найденной точке происходит смена знака второй производной. Следовательно, эта точка является точкой перегиба.

   Пример 4

Найти точки перегиба функции \(f\left( x \right) = {e^{ - {x^2}}}.\) Вычислим производные: \[ {f'\left( x \right) = {\left( {{e^{ - {x^2}}}} \right)^\prime } } = {{e^{ - {x^2}}} \cdot {\left( { - {x^2}} \right)^\prime } } = { - 2x{e^{ - {x^2}}};} \] \[ {f''\left( x \right) = {\left( { - 2x{e^{ - {x^2}}}} \right)^\prime } } = {{\left( { - 2x} \right)^\prime }{e^{ - {x^2}}} + \left( { - 2x} \right){\left( {{e^{ - {x^2}}}} \right)^\prime } } = { - 2{e^{ - {x^2}}} - 2x{e^{ - {x^2}}} \cdot \left( { - 2x} \right) } = { - 2{e^{ - {x^2}}} + 4{x^2}{e^{ - {x^2}}} } = {4{e^{ - {x^2}}}\left( {{x^2} - \frac{1}{2}} \right).} \] Вторая производная равна нулю в следующих точках: \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow 4{e^{ - {x^2}}}\left( {{x^2} - \frac{1}{2}} \right) = 0,}\;\; {\Rightarrow {x^2} - \frac{1}{2} = 0,}\;\; {\Rightarrow {x_{1,2}} = \pm \frac{1}{{\sqrt 2 }}.} \] При переходе через точки \({x_1} = -\large\frac{1}{{\sqrt 2 }}\normalsize,\) \({x_2} = \large\frac{1}{{\sqrt 2 }}\normalsize\) вторая производная меняет знак (рисунок \(3\)). Следовательно, указанные точки являются точками перегиба.

   Пример 5

Найти точки перегиба функции \(f\left( x \right) = {e^{\sin x}}.\) Определим производные заданной функции: \[ {f'\left( x \right) = {\left( {{e^{\sin x}}} \right)^\prime } } = {{e^{\sin x}}{\left( {\sin x} \right)^\prime } } = {{e^{\sin x}}\cos x;} \] \[ {f''\left( x \right) = {\left( {{e^{\sin x}}\cos x} \right)^\prime } } = {{\left( {{e^{\sin x}}} \right)^\prime }\cos x + {e^{\sin x}}{\left( {\cos x} \right)^\prime } } = {{e^{\sin x}}{\cos ^2}x - {e^{\sin x}}\sin x } = {{e^{\sin x}}\left( {{{\cos }^2}x - \sin x} \right).} \] Точки перегиба должны удовлетворять уравнению \(f''\left( x \right) = 0.\) Тогда \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow {e^{\sin x}}\left( {{{\cos }^2}x - \sin x} \right) = 0,}\;\; {\Rightarrow {\cos ^2}x - \sin x = 0,}\;\; {\Rightarrow 1 - {\sin ^2}x - \sin x = 0,}\;\; {\Rightarrow {\sin ^2}x + \sin x - 1 = 0.} \] Данное тригонометрическое уравнение из школьного курса математики решается с помощью замены \(\sin x = t.\) Следовательно, \[ {{t^2} + t - 1 = 0,}\;\; {\Rightarrow D = 1 - 4 \cdot \left( { - 1} \right) = 5,}\;\; {\Rightarrow {t_{1,2}} = \frac{{ - 1 \pm \sqrt 5 }}{2}.} \] Первый корень \({t_1}\) со знаком минус в числителе нужно отбросить, поскольку \({t_1} < -1.\) Тогда уравнение имеет следующее единственное решение: \[ {t = \frac{{ - 1 + \sqrt 5 }}{2} = \frac{{\sqrt 5 - 1}}{2},}\;\; {\Rightarrow \sin x = t = \frac{{\sqrt 5 - 1}}{2},}\;\; {\Rightarrow {x_n} = {\left( { - 1} \right)^n}\arcsin \frac{{\sqrt 5 - 1}}{2},\;n \in Z.} \] Итак, мы получили бесконечное множество точек, в которых вторая производная функции равна нулю. В пределах отрезка \(\left[ {0,2\pi } \right]\) существуют два решения, равные \[ {{x_1} = \arcsin \frac{{\sqrt 5 - 1}}{2} \approx 0,66;}\;\; {{x_2} = \pi - \arcsin \frac{{\sqrt 5 - 1}}{2} \approx 2,48.} \] Остальные решения \({x_n}\) образуются вследствие периодичности синуса и, следовательно, всей функции \(f\left( x \right).\)

Оба решения \({x_1}\) и \({x_2}\) соответствуют правому корню квадратного уравнения. Ясно, что при пересечении корня (в случае двух различных действительных корней) квадратичная функция меняет знак. Поэтому вторая производная, имеющая вид \[ {f''\left( x \right) } = {{e^{\sin x}}\left( {{{\cos }^2}x - \sin x} \right) } = {{e^{\sin x}}\left( { - {\sin^2}x - \sin x + 1} \right),} \] также меняет знак при переходе через точки \({x_n}.\) Отсюда, в соответствии с первым достаточным признаком, вытекает, что все найденные точки \({x_n}\) являются точками перегиба. Схематический вид функции на отрезке \(\left[ {0,2\pi } \right]\) показан на рисунке \(4\).

   Пример 6

При каких значениях \(a\) и \(b\) точка \(\left( { - 1,2} \right)\) является точкой перегиба графика функции \(y\left( x \right) = a{x^3} + b{x^2}?\) Первая и вторая производные заданной кубической функции выражаются формулами: \[ {y'\left( x \right) = {\left( {a{x^3} + b{x^2}} \right)^\prime } } = {3a{x^2} + 2bx,} \] \[ {y''\left( x \right) = {\left( {3a{x^2} + 2bx} \right)^\prime } } = {6ax + 2b.} \] В точке перегиба вторая производная равна нулю, т.е. первое уравнение имеет вид: \[6ax + 2b = 0\;\;\text{или}\;\;3ax + b = 0.\] Вторым уравнением служит уравнение самой функции. В результате получаем следующую систему для определения \(a\) и \(b\): \[\left\{ \begin{array}{l} 3ax + b = 0\\ a{x^3} + b{x^2} = y \end{array} \right..\] Подставим известные координаты точки перегиба графика функции: \[ {\left\{ \begin{array}{l} 3a \cdot \left( { - 1} \right) + b = 0\\ a \cdot {\left( { - 1} \right)^3} + b \cdot {\left( { - 1} \right)^2} = y \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} b - 3a = 0\\ b - a = 2 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} 2a = 2\\ b = a + 2 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} a = 1\\ b = 3 \end{array} \right..} \] Убедимся с помощью второго достаточного признака, что точка перегиба определена корректно. Проверим, что третья производная не равна нулю: \[y'''\left( x \right) = {\left( {6ax + 2b} \right)^\prime } = 6a \ne 0\;\;\text{при}\;\;a = 1.\] Следовательно, заданная точка \(\left( { - 1,2} \right)\) является точкой перегиба графика функции \(y\left( x \right) = -{x^3} + 2{x^2}.\)

   Пример 7

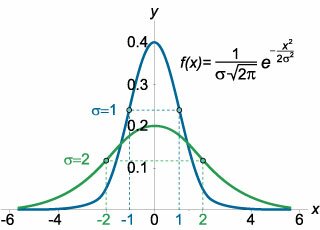
Найти точки перегиба функции Гаусса. Функция Гаусса или функция плотности нормального распределения определяется формулой \[f\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \large\frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}\normalsize}},\] где \(\mu\) − математическое ожидание, \(\sigma\) − среднеквадратичное отклонение распределения. Далее будем считать, что \(\mu = 0.\) Вычислим первую производную: \[ {f'\left( x \right) = {\left( {\frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}}\normalsize}} \right)^\prime } } = {\frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} \cdot {\left( { - \frac{{{x^2}}}{{2{\sigma ^2}}}} \right)^\prime } } = {\frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} \cdot \left( { - \frac{{2x}}{{2{\sigma ^2}}}} \right) } = { - \frac{x}{{{\sigma ^3}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}.} \] Продолжая дифференцирование, находим вторую производную: \[ {f''\left( x \right) = {\left( { - \frac{x}{{{\sigma ^3}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}} \right)^\prime } } = {{\left( { - \frac{x}{{{\sigma ^3}\sqrt {2\pi } }}} \right)^\prime }{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} } - {\frac{x}{{{\sigma ^3}\sqrt {2\pi } }}{\left( {{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}} \right)^\prime } } = {\left( { - \frac{1}{{{\sigma ^3}\sqrt {2\pi } }}} \right){e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} } - {\frac{x}{{{\sigma ^3}\sqrt {2\pi } }}\left( {{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}} \right) \cdot \left( { - \frac{x}{{{\sigma ^2}}}} \right) } = { - \frac{1}{{{\sigma ^3}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} } + {\frac{{{x^2}}}{{{\sigma ^5}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}} } = {\frac{1}{{{\sigma ^3}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}\left( {\frac{{{x^2}}}{{{\sigma ^2}}} - 1} \right).} \] Корни второй производной равны \[ {f''\left( x \right) = 0,}\;\; {\Rightarrow \frac{1}{{{\sigma ^3}\sqrt {2\pi } }}{e^{ - \large\frac{{{x^2}}}{{2{\sigma ^2}}}\normalsize}}\left( {\frac{{{x^2}}}{{{\sigma ^2}}} - 1} \right) = 0,}\;\; {\Rightarrow \frac{{{x^2}}}{{{\sigma ^2}}} - 1 = 0,}\;\; {\Rightarrow {x^2} = {\sigma ^2},}\;\; {\Rightarrow {x_{1,2}} = \pm \sigma .} \] Поскольку знак второй производной определяется квадратичным выражением \({x^2} - {\sigma ^2}.\) то ясно, что при переходе через точки \(x = \pm \sigma \) вторая производная будет менять свой знак. Поэтому, в соответствии с первым достаточным признаком, точки \(x = \pm \sigma \) являются точками перегиба. Схематический вид функции Гаусса при \(\sigma = 1\) и \(\sigma = 2\) приведен на рисунке \(5.\)

   Пример 8

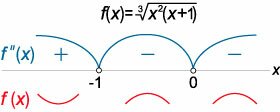
Найти точки перегиба функции \[f\left( x \right) = \sqrt[\large 3\normalsize]{{{x^2}\left( {x + 1} \right)}}.\] Вычислим сначала первую производную: \[ {f'\left( x \right) = {\left( {\sqrt[\large 3\normalsize]{{{x^2}\left( {x + 1} \right)}}} \right)^\prime } } = {{\left[ {{{\left( {{x^2}\left( {x + 1} \right)} \right)}^{\large\frac{1}{3}\normalsize}}} \right]^\prime } } = {\frac{1}{3}{\left( {{x^2}\left( {x + 1} \right)} \right)^{ - \large\frac{2}{3}\normalsize}} \cdot {\left( {{x^2}\left( {x + 1} \right)} \right)^\prime } } = {\frac{1}{{3\sqrt[\large 3\normalsize]{{{{\left( {{x^2}\left( {x + 1} \right)} \right)}^2}}}}} \cdot \left( {2x\left( {x + 1} \right) + {x^2}} \right) } = {\frac{{2{x^2} + 2x + {x^2}}}{{3\sqrt[\large 3\normalsize]{{{{\left( {{x^2}\left( {x + 1} \right)} \right)}^2}}}}} } = {\frac{{3{x^2} + 2x}}{{3\sqrt[\large 3\normalsize]{{{{\left( {{x^2}\left( {x + 1} \right)} \right)}^2}}}}} } = {\frac{{x\left( {3x + 2} \right)}}{{3x\sqrt[\large 3\normalsize]{{x{{\left( {x + 1} \right)}^2}}}}} } = {\frac{{3x + 2}}{{3\sqrt[\large 3\normalsize]{{x{{\left( {x + 1} \right)}^2}}}}}.} \] Продолжая дифференцирование, определяем вторую производную: \[ {f''\left( x \right) } = {{\left( {\frac{{3x + 2}}{{3\sqrt[\large 3\normalsize]{{x{{\left( {x + 1} \right)}^2}}}}}} \right)^\prime } } = {\frac{1}{3}{\left( {\frac{{3x + 2}}{{{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{1}{3}\normalsize}}}}} \right)^\prime } } = {\frac{1}{3} \cdot \frac{{{{\left( {3x + 2} \right)}^\prime }{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{1}{3}\normalsize}} - \left( {3x + 2} \right){{\left[ {{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{1}{3}\normalsize}}} \right]}^\prime }}}{{{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{2}{3}\normalsize}}}} } = {\frac{1}{3} \cdot \frac{{3{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{1}{3}\normalsize}} - \left( {3x + 2} \right) \cdot \frac{1}{3}{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{ - \large\frac{2}{3}\normalsize}} \cdot {{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^\prime }}}{{{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{2}{3}\normalsize}}}} } = {\frac{1}{3} \cdot \frac{{3x{{\left( {x + 1} \right)}^2} - \frac{1}{3}\left( {3x + 2} \right)\left[ {{{\left( {x + 1} \right)}^2} + 2x\left( {x + 1} \right)} \right]}}{{{{\left( {x{{\left( {x + 1} \right)}^2}} \right)}^{\large\frac{4}{3}\normalsize}}}} } = {\frac{1}{3} \cdot \frac{{\left( {x + 1} \right)\left\{ {3x\left( {x + 1} \right) - \left( {x + \frac{2}{3}} \right)\left( {3x + 1} \right)} \right\}}}{{{x^{\large\frac{4}{3}\normalsize}}{{\left( {x + 1} \right)}^{\large\frac{8}{3}\normalsize}}}} } = {\frac{1}{3} \cdot \frac{{3{x^2} + 3x - 3{x^2} - 2x - x - \frac{2}{3}}}{{{x^{\large\frac{4}{3}\normalsize}}{{\left( {x + 1} \right)}^{\large\frac{5}{3}\normalsize}}}} } = { - \frac{2}{{9\sqrt[\large 3\normalsize]{{{x^4}{{\left( {x + 1} \right)}^5}}}}}.} \] Видно, что вторая производная нигде не равна нулю. Однако точки перегиба могут быть при \(x = - 1\) и \(x = 0,\) где знаменатель равен нулю и вторая производная не существует. Исследуем знак второй производной при переходе через эти точки (рисунок \(6\)).

Таким образом, при переходе через точку \(x = - 1\) вторая производная меняет знак с плюса на минус. Следовательно, эта точка является точкой перегиба. Другая точка \(x = 0\) не является точкой перегиба, поскольку в ее окрестности знак второй производной не меняется.

   Пример 9

Найти точки перегиба кривой, заданной параметрически: \[x = {t^2},\;\;y = t + {t^3}.\] Первая производная \({y'_x}\) параметрической функции определяется по формуле \[{y'_x} = \frac{{{y'_t}}}{{{x'_t}}}.\] Подставляя заданные выражения \(x\left( t \right),\) \(x\left( t \right),\) получаем: \[ {{y'_x} = \frac{{{y'_t}}}{{{x'_t}}} } = {\frac{{{{\left( {t + {t^3}} \right)}^\prime }}}{{{{\left( {{t^2}} \right)}^\prime }}} } = {\frac{{1 + 3{t^2}}}{{2t}}.} \] Аналогично находится вторая производная \({y''_{xx}}:\) \[ {{y''_{xx}} = \frac{{{{\left( {{y'_x}} \right)}'_t}}}{{{x'_t}}} } = {\frac{{{{\left( {\frac{{1 + 3{t^2}}}{{2t}}} \right)}^\prime }}}{{{{\left( {{t^2}} \right)}^\prime }}} } = {\frac{{\frac{{6t \cdot 2t - \left( {1 + 3{t^2}} \right) \cdot 2}}{{4{t^2}}}}}{{2t}} } = {\frac{{12{t^2} - 2 - 6{t^2}}}{{8{t^3}}} } = {\frac{{6{t^2} - 2}}{{8{t^3}}} } = {\frac{{3{t^2} - 1}}{{4{t^3}}}.} \] Найдем значения параметра \(t,\) при которых вторая производная равна нулю: \[ {{y''_{xx}} = 0,}\;\; {\Rightarrow \frac{{3{t^2} - 1}}{{4{t^3}}} = 0,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {3{t^2} - 1 = 0}\\ {4{t^3} = 0} \end{array}} \right.,}\;\; {\Rightarrow {t^2} = \frac{1}{3},}\;\; {\Rightarrow {t_{1,2}} = \pm \frac{1}{{\sqrt 3 }}.} \] Чтобы выяснить, соответствуют ли найденные значения \({t_1},\) \({t_2}\) точкам перегиба, вычислим третью производную (то есть применим второй достаточный признак существования точки перегиба): \[ {{y'''_{xxx}} } = {\frac{{{{\left( {{y''_{xx}}} \right)}'_t}}}{{{x'_t}}} } = {\frac{{{{\left( {\frac{{3{t^2} - 1}}{{4{t^3}}}} \right)}^\prime }}}{{{{\left( {{t^2}} \right)}^\prime }}} } = {\frac{{\frac{{6t \cdot 4{t^2} - \left( {3{t^2} - 1} \right) \cdot 12{t^2}}}{{16{t^2}}}}}{{2t}} } = {\frac{{24{t^4} - 36{t^4} + 12{t^2}}}{{32{t^7}}} } = {\frac{{12{t^2} - 12{t^4}}}{{32{t^7}}} } = {\frac{{3 - 3{t^2}}}{{8{t^5}}}.} \] При подстановке значений \({t_{1,2}} = \pm \large\frac{1}{{\sqrt 3 }}\normalsize\) третья производная на равна нулю. Поэтому, согласно второму достаточному признаку, кривая имеет точки перегиба при \({t_{1,2}} = \pm \large\frac{1}{{\sqrt 3 }}\normalsize.\)

Вычислим координаты \(x\) и \(y\) точек перегиба: \[ {x\left( { - \frac{1}{{\sqrt 3 }}} \right) } = {{\left( { - \frac{1}{{\sqrt 3 }}} \right)^2} } = {\frac{1}{3} \approx 0,33;} \] \[ {y\left( { - \frac{1}{{\sqrt 3 }}} \right) } = { - \frac{1}{{\sqrt 3 }} + {\left( { - \frac{1}{{\sqrt 3 }}} \right)^2} } = { - \frac{1}{{\sqrt 3 }} - \frac{1}{{3\sqrt 3 }} } = {\frac{{ - 3 - 1}}{{3\sqrt 3 }} } = { - \frac{4}{{3\sqrt 3 }} \approx - 0,77;} \] \[ {x\left( { \frac{1}{{\sqrt 3 }}} \right) } = {{\left( {\frac{1}{{\sqrt 3 }}} \right)^2} } = {\frac{1}{3} \approx 0,33;} \] \[ {y\left( {\frac{1}{{\sqrt 3 }}} \right) } = {\frac{1}{{\sqrt 3 }} + {\left( {\frac{1}{{\sqrt 3 }}} \right)^2} } = {\frac{1}{{\sqrt 3 }} + \frac{1}{{3\sqrt 3 }} } = {\frac{{3 + 1}}{{3\sqrt 3 }} } = {\frac{4}{{3\sqrt 3 }} \approx 0,77.} \] На рисунке \(7\) схематически показана заданная кривая и отмечены ее точки перегиба. Как видно, она состоит из двух ветвей, симметричных относительно оси \(Ox.\)

   Пример 10

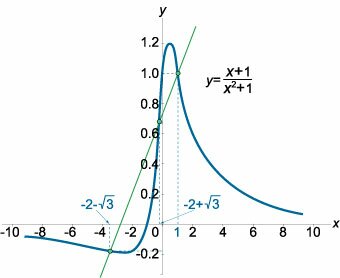
Показать, что график функции \(y = \large\frac{{x + 1}}{{{x^2} + 1}}\normalsize\) имеет три точки перегиба, лежащие на одной прямой. Следуя общей схеме, найдем последовательно первую и вторую производную: \[ {y'\left( x \right) = {\left( {\frac{{x + 1}}{{{x^2} + 1}}} \right)^\prime } } = {\frac{{{{\left( {x + 1} \right)}^\prime }\left( {{x^2} + 1} \right) - \left( {x + 1} \right){{\left( {{x^2} + 1} \right)}^\prime }}}{{{{\left( {{x^2} + 1} \right)}^2}}} } = {\frac{{{x^2} + 1 - 2x\left( {x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} } = {\frac{{{x^2} + 1 - 2{x^2} - 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} } = {\frac{{ - {x^2} - 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}};} \] \[ {y''\left( x \right) = {\left( {\frac{{ - {x^2} - 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} \right)^\prime } } = {\frac{{{{\left( { - {x^2} - 2x + 1} \right)}^\prime }{{\left( {{x^2} + 1} \right)}^2} - \left( { - {x^2} - 2x + 1} \right){{\left( {{{\left( {{x^2} + 1} \right)}^2}} \right)}^\prime }}}{{{{\left( {{x^2} + 1} \right)}^4}}} } = {\frac{{\left( { - 2x - 2} \right){{\left( {{x^2} + 1} \right)}^2} - 4x\left( {{x^2} + 1} \right)\left( { - {x^2} - 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^4}}} } = {\frac{{\left( { - 2x - 2} \right)\left( {{x^2} + 1} \right) - 4x\left( { - {x^2} - 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}} } = {\frac{{ - \color{blue}{2{x^3}} - \color{red}{2{x^2}} - \color{green}{2x} - \color{maroon}{2} + \color{blue}{4{x^3}} + \color{red}{8{x^2}} - \color{green}{4x}}}{{{{\left( {{x^2} + 1} \right)}^3}}} } = {\frac{{2\left( {\color{blue}{x^3} + \color{red}{3{x^2}} - \color{green}{3x} - \color{maroon}{1}} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}.} \] Кубический многочлен в числителе раскладывается следующим образом: \[ {{x^3} + 3{x^2} - 3x - 1 } = {{x^3} - {x^2} + 4{x^2} - 4x + x - 1 } = {{x^2}\left( {x - 1} \right) + 4x\left( {x - 1} \right) + x - 1 } = {\left( {x - 1} \right)\left( {{x^2} + 4x + 1} \right).} \] Разложим также квадратичную функцию на множители: \[ {{x^2} + 4x + 1 = 0,}\;\; {\Rightarrow D = 16 - 4 = 12,}\;\; {\Rightarrow {x_{1,2}} } = {\frac{{ - 4 \pm \sqrt {12} }}{2} = - 2 \pm \sqrt 3 .} \] Следовательно, вторая производная исходной функции записывается как \[ {y''\left( x \right) = \frac{{2\left( {{x^3} + 3{x^2} - 3x - 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}} } = {\frac{{2\left( {x - 1} \right)\left( {x + 2 + \sqrt 3 } \right)\left( {x + 2 - \sqrt 3 } \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}.} \] Таким образом, вторая производная имеет три корня: \[ {{x_1} = 1,}\;\;\; {{x_2} = - 2 - \sqrt 3 ,}\;\;\; {{x_3} = - 2 + \sqrt 3 ,} \] причем при переходе через каждую из этих точек вторая производная меняет знак, то есть найденные точки являются точками перегиба.

Вычислим соответствующие значения \(y:\) \[{y_1} = y\left( 1 \right) = \frac{{1 + 1}}{{{1^2} + 1}} = 1;\] \[ {{y_2} = y\left( { - 2 - \sqrt 3 } \right) } = {\frac{{ - 2 - \sqrt 3 + 1}}{{{{\left( { - 2 - \sqrt 3 } \right)}^2} + 1}} } = {\frac{{ - 1 - \sqrt 3 }}{{4 + 4\sqrt 3 + 3 + 1}} } = {\frac{{ - 1 - \sqrt 3 }}{{8 + 4\sqrt 3 }} } = {\frac{{ - 1 - \sqrt 3 }}{{4\left( {2 + \sqrt 3 } \right)}} } = {\frac{{\left( { - 1 - \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right)}}{{4\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right)}} } = {\frac{{ - 2 - 2\sqrt 3 + \sqrt 3 + 3}}{{4\left( {4 - 3} \right)}} } = {\frac{{1 - \sqrt 3 }}{4};} \] \[ {{y_2} = y\left( { - 2 + \sqrt 3 } \right) } = {\frac{{ - 2 + \sqrt 3 + 1}}{{{{\left( { - 2 + \sqrt 3 } \right)}^2} + 1}} } = {\frac{{ - 1 + \sqrt 3 }}{{4 - 4\sqrt 3 + 3 + 1}} } = {\frac{{ - 1 + \sqrt 3 }}{{8 - 4\sqrt 3 }} } = {\frac{{ - 1 + \sqrt 3 }}{{4\left( {2 - \sqrt 3 } \right)}} } = {\frac{{\left( { - 1 + \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}{{4\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} } = {\frac{{ - 2 + 2\sqrt 3 - \sqrt 3 + 3}}{{4\left( {4 - 3} \right)}} } = {\frac{{1 + \sqrt 3 }}{4}.} \] Итак, точки перегиба графика функции имеют такие координаты: \[ {\left( {1,1} \right),}\;\;\; {\left( { - 2 - \sqrt 3 ,\frac{{1 - \sqrt 3 }}{4}} \right),}\;\;\; {\left( { - 2 + \sqrt 3 ,\frac{{1 + \sqrt 3 }}{4}} \right).} \] Убедимся, что эти три точки лежат на одной прямой. В этом случае должно выполняться пропорциональное соотношение \[\frac{{{y_3} - {y_2}}}{{{y_3} - {y_1}}} = \frac{{{x_3} - {x_2}}}{{{x_3} - {x_1}}}.\] Подставляем найденные координаты: \[\require{cancel} {\frac{{\frac{{1 + \sqrt 3 }}{4} - \frac{{1 - \sqrt 3 }}{4}}}{{\frac{{1 + \sqrt 3 }}{4} - 1}} = \frac{{ - 2 + \sqrt 3 - \left( { - 2 - \sqrt 3 } \right)}}{{ - 2 + \sqrt 3 - 1}},}\;\; {\Rightarrow \frac{{\frac{{\cancel{1} + \sqrt 3 - \cancel{1} + \sqrt 3 }}{4}}}{{\frac{{1 + \sqrt 3 - 4}}{4}}} = \frac{{ - \cancel{2} + \sqrt 3 + \cancel{2} + \sqrt 3 }}{{\sqrt 3 - 3}},}\;\; {\Rightarrow \frac{{2\sqrt 3 }}{{\sqrt 3 - 3}} = \frac{{2\sqrt 3 }}{{\sqrt 3 - 3}}.} \] Это доказывает, что точки перегиба расположены на одной прямой. Схематически график функции показан на рисунке \(8.\)