Теорема Стокса

Пусть \(S\) является гладкой поверхностью, ограниченной гладкой кривой \(C.\) Тогда для любой непрерывно дифференцируемой векторной функции \[\mathbf{F}\left( {x,y,z} \right) = \left( {P\left( {x,y,z} \right),Q\left( {x,y,z} \right),R\left( {x,y,z} \right)} \right)\] справедлива теорема Стокса: \[\oint\limits_C {\mathbf{F} \cdot d\mathbf{r}} = \iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} ,\] где \[ {\nabla \times \mathbf{F} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ {\frac{\partial }{{\partial x}}}&{\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial z}}}\\ P&Q&R \end{array}} \right| } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right)\mathbf{i} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right)\mathbf{j} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)\mathbf{k} } \] − ротор векторного поля \(\mathbf{F}.\)

Символ \(\oint\limits{}\) показывает, что криволинейный интеграл вычисляется по замкнутой кривой.

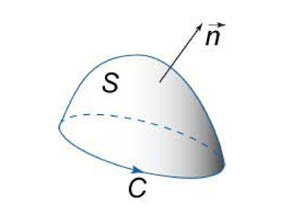
Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали \(\mathbf{n}\) (рисунок \(1\)).

Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.

В координатной форме теорема Стокса может быть записана в следующем виде: \[ {\oint\limits_C {Pdx + Qdy + Rdz} } = {\iint\limits_S {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right)dydz + \left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right)dzdx + \left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} .} \]

   Пример 1

Показать, что криволинейный интеграл \(\oint\limits_C {yzdx + xzdy + xydz} \) равен \(0\) вдоль любого замкнутого контура \(C.\) Обозначим через \(S\) поверхность, ограниченную замкнутой кривой \(C.\) Применяя формулу Стокса, можно записать \[P = yz,\;\;Q = xz,\;\;R = xy.\] Тогда \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {x - x} \right)\mathbf{i} + \left( {y - y} \right)\mathbf{j} + \left( {z - z} \right)\mathbf{k} } = {0 \cdot \mathbf{i} + 0 \cdot \mathbf{j} + 0 \cdot \mathbf{k} = \mathbf{0}.} \] Следовательно, находим значение криволинейного интеграла: \[ {\oint\limits_C {yzdx + xzdy + xydz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\mathbf{0} \cdot d\mathbf{S}} = 0.} \] Утверждение доказано.

   Пример 2

Используя формулу Стокса, вычислить криволинейный интеграл \(\oint\limits_C {\left( {y + 2z} \right)dx + \left( {x + 2z} \right)dy + \left( {x + 2y} \right)dz},\) где кривая \(C\) образована пересечением сферы \({x^2} + {y^2} + {z^2} = 1\) плоскостью \(x + 2y + 2z = 0.\) Обозначим через \(S\) круг, вырезаемый из заданной плоскости при пересечении со сферой. Определим координаты единичного вектора нормали \(\mathbf{n}\) к поверхности \(S:\) \[ {\mathbf{n} = \frac{{1 \cdot \mathbf{i} + 2 \cdot \mathbf{j} + 2 \cdot \mathbf{k}}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} } = {\frac{1}{3}\mathbf{i} + \frac{2}{3}\mathbf{j} + \frac{2}{3}\mathbf{k}.} \] В нашем случае \[P = y + 2z,\;\;Q = x + 2z,\;\;R = x + 2y.\] Следовательно, ротор вектора \(\mathbf{F}\) равен \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {2 - 2} \right){\mathbf{i}} + \left( {2 - 1} \right){\mathbf{j}} + \left( {1 - 1} \right){\mathbf{k}} } = {{\bf{j}}.} \] По теореме Стокса получаем \[ {\oint\limits_C {\left( {y + 2z} \right)dx + \left( {x + 2z} \right)dy + \left( {x + 2y} \right)dz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot \mathbf{n}dS} } = {\iint\limits_S {\mathbf{j} \cdot \left( {\frac{1}{3}\mathbf{i} + \frac{2}{3}\mathbf{j} + \frac{2}{3}\mathbf{k}} \right)dS} } = {\frac{2}{3}\iint\limits_S {dS} .} \] Поскольку центр сферы \({x^2} + {y^2} + {z^2} = 1\) находится в начале координат, а плоскость \(x + 2y + 2z = 0\) также проходит через начало координат, то сечением будет являться круг радиусом \(1.\) Тогда интеграл имеет значение \[I = \frac{2}{3}\iint\limits_S {dS} = \frac{2}{3} \cdot \pi \cdot {1^2} = \frac{{2\pi }}{3}.\]

   Пример 3

Используя теорему Стокса, найти криволинейный интеграл \(\oint\limits_C {{y^3}dx - {x^3}dy + {z^3}dz}.\) Кривая \(C\) представляет собой пересечение цилиндра \({x^2} + {y^2} = {a^2}\) и плоскости \(x + y + z = b.\) Обозначим через \(S\) часть плоскости, вырезаемую цилиндром. Пусть обход кривой \(C\) осуществляется против часовой стрелки, если смотреть из конечной точки вектора нормали \(\mathbf{n},\) координаты которого равны \[ {\mathbf{n} = \frac{{1 \cdot \mathbf{i} + 1 \cdot \mathbf{j} + 1 \cdot \mathbf{k}}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} } = {\frac{1}{{\sqrt 3 }}\mathbf{i} + \frac{1}{{\sqrt 3 }}\mathbf{j} + \frac{1}{{\sqrt 3 }}\mathbf{k}.} \] Так как \(P = {y^3},\) \(Q = -{x^3},\) \(R = {z^3},\) то можно записать \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {0 - 0} \right){\mathbf{i}} + \left( {0 - 0} \right){\mathbf{j}} + \left( { - 3{x^2} - 3{y^2}} \right){\mathbf{k}} } = { - 3\left( {{x^2} + {y^2}} \right)\mathbf{k}.} \] Далее, применяя формулу Стокса, находим \[ {\oint\limits_C {{y^3}dx - {x^3}dy + {z^3}dz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot \mathbf{n}dS} } = {\iint\limits_S {\left( { - 3\left( {{x^2} + {y^2}} \right)\mathbf{k}} \right) \cdot \left( {\frac{1}{{\sqrt 3 }}\mathbf{i} + \frac{1}{{\sqrt 3 }}\mathbf{j} + \frac{1}{{\sqrt 3 }}\mathbf{k}} \right)dS} } = { - \sqrt 3 \iint\limits_S {\left( {{x^2} + {y^2}} \right)dS} } = { - \sqrt 3 {a^2}\iint\limits_S {dS} .} \] Проекция поверхности \(S\) на плоскость \(Oxy\) представляет собой круг \({x^2} + {y^2} = {a^2}\) радиуса \(a.\) Поэтому, записывая уравнение плоскости в виде \(z = b - x - y\) и используя формулу \[ {\iint\limits_S {dS} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} ,} \] получаем \[ {I = - \sqrt 3 {a^2}\iint\limits_S {dS} } = { - \sqrt 3 {a^2}\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} dxdy} } = { - 3{a^2}\iint\limits_{D\left( {x,y} \right)} {dxdy} } = { - 3{a^2} \cdot \pi {a^2} } = { - 3\pi {a^4}.} \]

   Пример 4

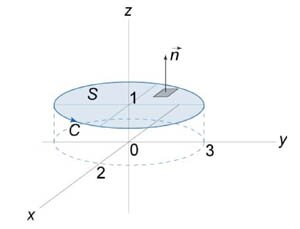
Вычислить криволинейный интеграл \(\oint\limits_C {\left( {x + z} \right)dx + \left( {x - y} \right)dy + xdz},\) используя теорему Стокса. Кривая \(C\) имеет форму эллипса и определяется уравнениями \(\large\frac{{{x^2}}}{4}\normalsize + \large\frac{{{y^2}}}{9}\normalsize = 1,\) \(z = 1\) (рисунок \(2\) выше). Пусть поверхность \(S\) − это часть плоскости \(z = 1,\) ограниченная эллипсом. Очевидно, единичный вектор нормали к данной поверхности будет \(\mathbf{n} = \mathbf{k}.\) Поскольку \[P = x + z,\;\;Q = x - y,\;\;R = x,\] то ротор поля \(\mathbf{F}\) равен \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {0 - 0} \right){\mathbf{i}} + \left( {1 - 1} \right){\mathbf{j}} + \left( {1 - 0} \right){\mathbf{k}} = \mathbf{k}.} \] В соответствии с теоремой Стокса получаем \[ {\oint\limits_C {\left( {x + z} \right)dx + \left( {x - y} \right)dy + xdz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot \mathbf{n}dS} } = {\iint\limits_S {\mathbf{k} \cdot \mathbf{k}dS} } = {\iint\limits_S {dS} .} \] Двойной интеграл в последней формуле равен площади эллипса. Поэтому интеграл равен \[\iint\limits_S {dS} = \pi \cdot 2 \cdot 3 = 6\pi .\]

   Пример 5

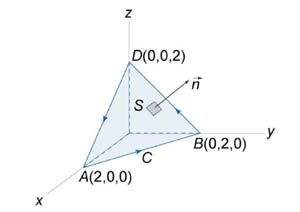
Используя теорему Стокса, вычислить криволинейный интеграл \(\oint\limits_C {\left( {z - y} \right)dx + \left( {x - z} \right)dy + \left( {y - x} \right)dz} .\) Кривая \(C\) представляет собой треугольник с вершинами \(A\left( {2,0,0} \right),\) \(B\left( {0,2,0} \right),\) \(D\left( {0,0,2} \right)\) (рисунок \(3\)). Пусть \(S\) будет плоскость треугольника \(ABD.\) Ориентация поверхности \(S\) и направление обхода контура \(C\) показаны ниже на рисунке \(3.\)

Определим сначала нормальный вектор \(\mathbf{n}.\) \[ {\overrightarrow{AB} = \left( {{x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A}} \right) } = {\left( {0 - 2,2 - 0,0 - 0} \right) } = {\left( { - 2,2,0} \right),} \] \[ {\overrightarrow{BD} = \left( {{x_D} - {x_B},{y_D} - {y_B},{z_D} - {z_B}} \right) } = {\left( {0 - 0,0 - 2,2 - 0} \right) } = {\left( { 0,-2,2} \right).} \] Тогда \[ {\overrightarrow{AB} \times \overrightarrow{BD} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ { - 2} & 2 & 0\\ 0 & { - 2} & 2 \end{array}} \right| } ={ 4\mathbf{i} + 4\mathbf{j} + 4\mathbf{k},} \] и, следовательно, \[ {\mathbf{n} = \frac{{\overrightarrow{AB} \times \overrightarrow{BD}}}{{\left| {\overrightarrow{AB} \times \overrightarrow{BD}} \right|}} } = {\frac{{4\mathbf{i} + 4\mathbf{j} + 4\mathbf{k}}}{{\sqrt {{4^2} + {4^2} + {4^2}} }} } = {\frac{1}{{\sqrt 3 }}\mathbf{i} + \frac{1}{{\sqrt 3 }}\mathbf{j} + \frac{1}{{\sqrt 3 }}\mathbf{k}.} \] В нашем случае \(P = z - y,\) \(Q = x - z,\) \(R = y - x,\) и ротор \(\mathbf{F}\) равен \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {1 - \left( { - 1} \right)} \right){\mathbf{i}} + \left( {1 - \left( { - 1} \right)} \right){\mathbf{j}} + \left( {1 - \left( { - 1} \right)} \right){\mathbf{k}} } = {2{\mathbf{i}} + 2{\mathbf{j}} + 2{\mathbf{k}}.} \] Применяя формулу Стокса, находим \[ {I = \oint\limits_C {\left( {z - y} \right)dx + \left( {x - z} \right)dy + \left( {y - x} \right)dz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot \mathbf{n}dS} } = {\iint\limits_S {\left( {2{\mathbf{i}} + 2{\mathbf{j}} + 2{\mathbf{k}}} \right) \cdot \left( {\frac{1}{{\sqrt 3 }}\mathbf{i} + \frac{1}{{\sqrt 3 }}\mathbf{j} + \frac{1}{{\sqrt 3 }}\mathbf{k}} \right)dS} } = {\frac{2}{{\sqrt 3 }}\iint\limits_S {\left( {1 + 1 + 1} \right)dS} } = {2\sqrt 3 \iint\limits_S {dS} .} \] Здесь двойной интеграл \(\iint\limits_S {dS} \) равен площади треугольника \(ABD,\) которая составляет \[ {{S_{ABD}} = \frac{1}{2}\left| {\overrightarrow{AB} \times \overrightarrow{BD}} \right| } = {\frac{1}{2} \cdot 4\sqrt 3 } = {2\sqrt 3 .} \] Таким образом, интеграл имеет значение \[I = 2\sqrt 3 \iint\limits_S {dS} = 2\sqrt 3 \cdot 2\sqrt 3 = 12.\]

   Пример 6

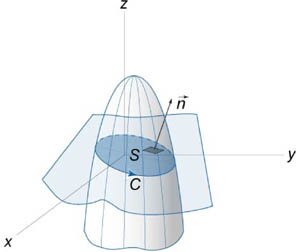
Найти интеграл \(\oint\limits_C {\left( {{z^2} - {y^2}} \right)dx + \left( {{x^2} - {z^2}} \right)dy + \left( {{y^2} - {x^2}} \right)dz} \) с использованием теоремы Стокса. Кривая \(C\) образована пересечением параболоида \(z = 5 - {x^2} - {y^2}\) с плоскостью \(x + y + z = 1\) (рисунок \(4\)). Пусть \(S\) будет часть плоскости, вырезанная параболоидом. Ориентация поверхности \(S\) и направление обхода контура \(C\) показаны на рисунке \(4.\) Из уравнения плоскости найдем вектор нормали \(\mathbf{n}:\) \[ {\mathbf{n} = \frac{{1 \cdot \mathbf{i} + 1 \cdot \mathbf{j} + 1 \cdot \mathbf{k}}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} } = {\frac{1}{{\sqrt 3 }}\mathbf{i} + \frac{1}{{\sqrt 3 }}\mathbf{j} + \frac{1}{{\sqrt 3 }}\mathbf{k}.} \] Так как \[P = {z^2} - {y^2},\;\;Q = {x^2} - {z^2},\;\;R = {y^2} - {x^2},\] то ротор векторного поля \(\mathbf{F}\) равен \[ {\nabla \times {\mathbf{F}} } = {\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right){\mathbf{i}} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right){\mathbf{j}} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right){\mathbf{k}} } = {\left( {2y + 2z} \right){\mathbf{i}} + \left( {2z + 2x} \right){\mathbf{j}} + \left( {2x + 2y} \right){\mathbf{k}}.} \] По теореме Стокса находим \[ {I = \oint\limits_C {\left( {{z^2} - {y^2}} \right)dx + \left( {{x^2} - {z^2}} \right)dy + \left( {{y^2} - {x^2}} \right)dz} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {\nabla \times \mathbf{F}} \right) \cdot \mathbf{n}dS} } = {\frac{2}{{\sqrt 3 }}\iint\limits_S {\left( {y + z + z + x + x + y} \right)dS} } = {\frac{4}{{\sqrt 3 }}\iint\limits_S {\left( {x + y + z} \right)dS} .} \] Поскольку \(x + y + z = 1,\) то интеграл становится равным \[I = \frac{4}{{\sqrt 3 }}\iint\limits_S {dS} .\] Чтобы завершить расчеты, нужно найти двойной интеграл \(\iint\limits_S {dS},\) то есть вычислить площадь поверхности \(S.\) Явное уравнение плоскости имеет вид \(z = 1 - x - y.\) Поэтому, по формуле \[ {\iint\limits_S {dS} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} ,} \] где \(D\left( {x,y} \right)\) − это проекция \(S\) на плоскость \(Oxy,\) получаем \[ {I = \frac{4}{{\sqrt 3 }}\iint\limits_S {dS} } = {\frac{4}{{\sqrt 3 }}\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} dxdy} } = {4\iint\limits_{D\left( {x,y} \right)} {dxdy} .} \] Определим область интегрирования \(D\left( {x,y} \right).\) Решая систему уравнений \[\left\{ \begin{array}{l} x + y + z = 1\\ z = 5 - {x^2} - {y^2} \end{array} \right.,\] находим: \[ {x + y + 5 - {x^2} - {y^2} = 1,}\;\; {\Rightarrow {x^2} + {y^2} - x - y = 4,}\;\; {\Rightarrow \left( {{x^2} - x + \frac{1}{4}} \right) + \left( {{y^2} - y + \frac{1}{4}} \right) = \frac{9}{2},}\;\; {\Rightarrow {\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {\frac{3}{{\sqrt 2 }}} \right)^2}.} \] Как видно, область \(D\left( {x,y} \right)\) − это круг радиуса \(R = \large\frac{3}{{\sqrt 2 }}\normalsize\) с центром в точке \(\left( {\large\frac{1}{2}\normalsize,\large\frac{1}{2}\normalsize} \right).\) Тогда площадь области \(D\left( {x,y} \right)\) равна \[\iint\limits_{D\left( {x,y} \right)} {dxdy} = \pi {\left( {\frac{3}{{\sqrt 2 }}} \right)^2} = \frac{{9\pi }}{2}.\] Отсюда находим окончательное значение интеграла: \[I = 4 \cdot \frac{{9\pi }}{2} = 18\pi .\]