Теорема Остроградского-Гаусса

Обозначим через \(G\) трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностью \(S\) с внешней нормалью. Предположим, что задано векторное поле \[\mathbf{F}\left( {x,y,z} \right) = \left( {P\left( {x,y,z} \right),Q\left( {x,y,z} \right),R\left( {x,y,z} \right)} \right),\] компоненты которого имеют непрерывные частные производные.

Согласно формуле Остроградского-Гаусса, \[\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} = \iiint\limits_G {\left( {\nabla \cdot \mathbf{F}} \right)dV} ,\] где через \[\nabla \cdot \mathbf{F} = \frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} + \frac{{\partial R}}{{\partial z}}\] обозначена дивергенция векторного поля \(\mathbf{F}\) (она обозначается также символом \(\text{div}\,\mathbf{F}\)), а поверхностный интеграл вычисляется по замкнутой поверхности.

Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами.

Данную формулу можно записать также в координатной форме: \[ {\iint\limits_S {Pdydz + Qdxdz + Rdxdy} } = {\iiint\limits_G {\left( {\frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} + \frac{{\partial R}}{{\partial z}}} \right)dxdydz} .} \] В частном случае, полагая \(P = x,\) \(Q = y,\) \(R = z,\) получаем формулу для вычисления объема тела \(G:\) \[V = \frac{1}{3}\left| {\iint\limits_S {xdydz + ydxdz + zdxdy} } \right|.\]

   Пример 1

Вычислить поверхностный интеграл \(\iint\limits_S {{x^3}dydz + {y^3}dxdz + {z^3}dxdy} ,\) где \(S\) − внешне ориентированная поверхность сферы, заданная уравнением \({x^2} + {y^2} + {z^2} = {a^2}.\) Используя формулу Остроградского-Гаусса, можно записать \[ {I = \iint\limits_S {{x^3}dydz + {y^3}dxdz + {z^3}dxdy} } = {\iiint\limits_G {\left( {3{x^2} + 3{y^2} + 3{z^2}} \right)dxdydz} } = {3\iiint\limits_G {\left( {{x^2} + {y^2} + {z^2}} \right)dxdydz} .} \] Вычислим полученный тройной интеграл в сферических интегралах. \[ {I = 3\iiint\limits_G {\left( {{x^2} + {y^2} + {z^2}} \right)dxdydz} } = {3\iiint\limits_G {{r^2} \cdot {r^2}\sin \theta drd\psi d\theta } } = {3\int\limits_0^{2\pi } {d\psi } \int\limits_0^\pi {\sin \theta d\theta } \int\limits_0^a {{r^4}dr} } = {3 \cdot 2\pi \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^\pi } \right] \cdot \left[ {\left. {\left( {\frac{{{r^5}}}{5}} \right)} \right|_0^a} \right] } = {\frac{{12\pi {a^5}}}{5}.} \]

   Пример 2

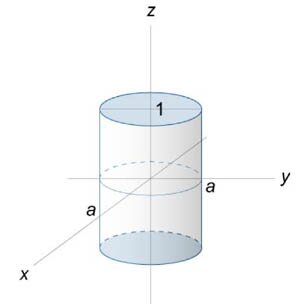
Применяя теорему Остроградского-Гаусса, вычислить поверхностный интеграл \(\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} \) от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {x,y,z} \right),\) где \(S\) − поверхность тела, образованного цилиндром \({x^2} + {y^2} = {a^2}\) и плоскостями \(z = -1,\) \(z = 1\) (рисунок \(1\)). В соответствии с формулой Остроградского-Гаусса, \[ {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iiint\limits_G {\left( {\nabla \cdot \mathbf{F}} \right)dV} } = {\iiint\limits_G {\left[ {\frac{\partial }{{\partial x}}\left( x \right) + \frac{\partial }{{\partial y}}\left( y \right) + \frac{\partial }{{\partial z}}\left( z \right)} \right]dxdydz} } = {\iiint\limits_G {\left( {1 + 1 + 1} \right)dxdydz} } = {3\iiint\limits_G {dxdydz} .} \] Вычисляя в цилиндрических координатах, получаем ответ: \[ {I = 3\iiint\limits_G {dxdydz} } = {3\int\limits_{ - 1}^1 {dz} \int\limits_0^{2\pi } {d\varphi } \int\limits_0^a {rdr} } = {3 \cdot 2 \cdot 2\pi \cdot \left[ {\left. {\left( {\frac{{{r^2}}}{2}} \right)} \right|_0^a} \right] } = {6\pi {a^2}.} \]

   Пример 3

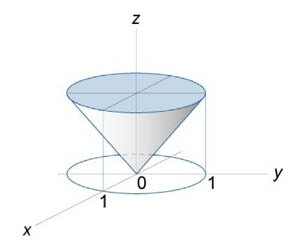
Используя формулу Остроградского-Гаусса, оценить поверхностный интеграл \(\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} \) от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {{x^3},{y^3},{z^3}} \right),\) где \(S\) − поверхность тела, ограниченного поверхностью \({x^2} + {y^2} - {z^2} = 0\) и плоскостью \(z = 1.\) Данное тело схематически изображено на рисунке \(2.\) Применяя теорему Остроградского-Гаусса, можно записать \[ {I = \iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iiint\limits_G {\left( {\nabla \cdot \mathbf{F}} \right)dV} } = {\iiint\limits_G {\left[ {\frac{\partial }{{\partial x}}\left( {{x^3}} \right) + \frac{\partial }{{\partial y}}\left( {{y^3}} \right) + \frac{\partial }{{\partial z}}\left( {{z^3}} \right)} \right]dxdydz} } = {3\iiint\limits_G {\left( {{x^2} + {y^2} + {z^2}} \right)dxdydz} .} \] Переходя к цилиндрическим координатам, получаем \[ {I = 3\iiint\limits_G {\left( {{x^2} + {y^2} + {z^2}} \right)dxdydz} } = {3\int\limits_0^1 {dz} \int\limits_0^{2\pi } {d\varphi } \int\limits_0^z {\left( {{r^2} + {z^2}} \right)rdr} } = {6\pi \int\limits_0^1 {\left[ {\left. {\left( {\frac{{{r^4}}}{4} + \frac{{{z^2}{r^2}}}{2}} \right)} \right|_{r = 0}^z} \right]dz} } = {6\pi \int\limits_0^1 {\frac{{3{z^4}}}{4}dz} } = {\frac{{9\pi }}{2} \cdot \left[ {\left. {\left( {\frac{{{z^5}}}{5}} \right)} \right|_0^1} \right] } = {\frac{{9\pi }}{{10}}.} \]

   Пример 4

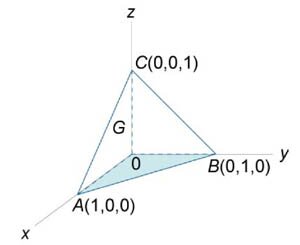
Вычислить поверхностный интеграл \(\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} \) от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {2xy, 8xz, 4yz} \right),\) где \(S\) является поверхностью тетраэдра с вершинами \(O\left( {0,0,0} \right),\) \(A\left( {1,0,0} \right),\) \(B\left( {0,1,0} \right),\) \(C\left( {0,0,1} \right)\) (рисунок \(3\)). По формуле Остроградского-Гаусса, \[ {I = \iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iiint\limits_G {\left( {\nabla \cdot \mathbf{F}} \right)dV} } = {\iiint\limits_G {\left[ {\frac{\partial }{{\partial x}}\left( {2xy} \right) + \frac{\partial }{{\partial y}}\left( {8xz} \right) + \frac{\partial }{{\partial z}}\left( {4yz} \right)} \right]dV} } = {\iiint\limits_G {\left( {2y + 0 + 4y} \right)dxdydz} } = {6\iiint\limits_G {ydxdydz} .} \] Вычислим полученный тройной интеграл. Уравнение прямой \(AB\) имеет вид \[ {\frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{x - {x_A}}}{{{x_B} - {x_A}}},}\;\; {\Rightarrow \frac{{y - 0}}{{1 - 0}} = \frac{{x - 1}}{{0 - 1}},}\;\; {\Rightarrow y = - \left( {x - 1} \right)\;\;\text{или}\;\;y = 1 - x.} \] А уравнение плоскости \(ABC\) равно \[ {\frac{x}{1} + \frac{y}{1} + \frac{z}{1} = 1,}\;\; {\Rightarrow x + y + z = 1\;\;\text{или}\;\;z = 1 - x - y.} \] Находим значение интеграла: \[ {I = 6\iiint\limits_G {ydxdydz} } = {6\int\limits_0^1 {dx} \int\limits_0^{1 - x} {dy} \int\limits_0^{1 - x - y} {ydz} } = {6\int\limits_0^1 {dx} \int\limits_0^{1 - x} {\left( {1 - x - y} \right)ydy} } = {6\int\limits_0^1 {dx} \int\limits_0^{1 - x} {\left[ {y\left( {1 - x} \right) - {y^2}} \right]dy} } = {6\int\limits_0^1 {\left[ {\left. {\left( {\left( {1 - x} \right)\frac{{{y^2}}}{2} - \frac{{{y^3}}}{3}} \right)} \right|_{y = 0}^{1 - x}} \right]dx} } = {6\int\limits_0^1 {\left[ {\frac{{{{\left( {1 - x} \right)}^3}}}{2} - \frac{{{{\left( {1 - x} \right)}^3}}}{3}} \right]dx} } = {6 \cdot \frac{1}{6}\int\limits_0^1 {{{\left( {1 - x} \right)}^3}dx} } = { - \int\limits_0^1 {{{\left( {1 - x} \right)}^3}d\left( {1 - x} \right)} } = { - \left. {\left( {\frac{{{{\left( {1 - x} \right)}^4}}}{4}} \right)} \right|_0^1 } = { - \left( {0 - \frac{1}{4}} \right) = \frac{1}{4}.} \]

   Пример 5

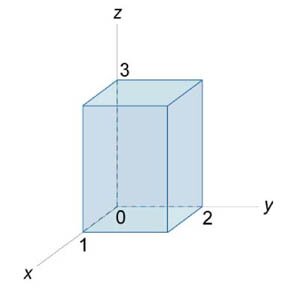
Вычислить поверхностный интеграл \(\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} \) от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {2{x^2}y,x{z^2},4yz} \right),\) где \(S\) − поверхность параллелепипеда, образованного плоскостями \(x = 0,\) \(x = 1,\) \(y = 0,\) \(y = 2,\) \(z = 0,\) \(z = 3\) (рисунок \(4\)). Воспользуемся теоремой Остроградского-Гаусса: \[ {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iint\limits_S {\left( {2{x^2}y \cdot \mathbf{i} + x{z^2} \cdot \mathbf{j} + 4yz \cdot \mathbf{k}} \right) \cdot d\mathbf{S}} } = {\iiint\limits_G {\left[ {\frac{\partial }{{\partial x}}\left( {2{x^2}y} \right) + \frac{\partial }{{\partial y}}\left( {x{z^2}} \right) + \frac{\partial }{{\partial z}}\left( {4yz} \right)} \right]dxdydz} } = {\iiint\limits_G {\left( {4xy + 4y} \right)dxdydz} } = {4\int\limits_0^1 {dx} \int\limits_0^2 {dy} \int\limits_0^3 {\left( {x + 1} \right)ydz} } = {4\int\limits_0^1 {dx} \int\limits_0^2 {\left[ {\left. {\left( {\left( {x + 1} \right)yz} \right)} \right|_{z = 0}^3} \right]dy} } = {12\int\limits_0^1 {dx} \int\limits_0^2 {\left( {x + 1} \right)ydy} } = {12\int\limits_0^1 {\left[ {\left. {\left( {\left( {x + 1} \right)\frac{{{y^2}}}{2}} \right)} \right|_{y = 0}^2} \right]dx} } = {24\int\limits_0^1 {\left( {x + 1} \right)dx} } = {24\left[ {\left. {\left( {\frac{{{x^2}}}{2} + x} \right)} \right|_0^1} \right] } = {24 \cdot \frac{3}{2} = 36.} \]

   Пример 6

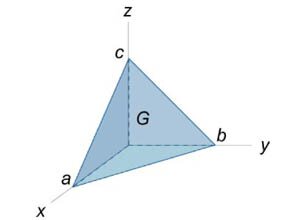
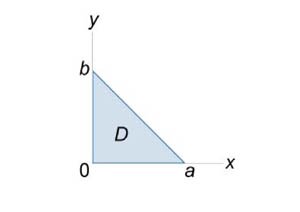
Найти интеграл \(\iint\limits_S {2xdydz + \left( {3y + x} \right)dxdz + \left( {2y + 4z} \right)dxdy} ,\) где \(S\) − внешняя поверхность пирамиды \(\large\frac{x}{a}\normalsize + \large\frac{y}{b}\normalsize + \large\frac{z}{c}\normalsize \le 1,\) \(x \ge 0,\) \(y \ge 0,\) \(z \ge 0.\) (рисунок \(5\)). Применяя формулу Остроградского-Гаусса можно записать искомый поверхностный интеграл в виде \[ {\iint\limits_S {2xdydz + \left( {3y + x} \right)dxdz + \left( {2y + 4z} \right)dxdy} } = {\iiint\limits_G {\left( {2 + 3 + 4} \right)dxdydz} } = {9\iiint\limits_G {dxdydz} .} \] Найдем тройной интеграл. Область интегрирования в плоскости \(xy\) показана на рисунке \(6.\) Полагая \(z = 0,\) получаем \[ {\frac{x}{a} + \frac{y}{b} \le 1,\;x \ge 0,\;y \ge 0,}\;\; {\Rightarrow \frac{y}{b} \le 1 - \frac{x}{a}\;\;\text{или}\;\;y \le b - \frac{b}{a}x.} \] Следовательно, область \(D\) можно представить в виде множества \[D = \left\{ {\left( {x,y} \right)\mid 0 \le x \le a,0 \le y \le b - \frac{b}{a}x} \right\}.\] Решая неравенство \(\large\frac{x}{a}\normalsize + \large\frac{y}{b}\normalsize + \large\frac{z}{c}\normalsize \le 1\) относительно переменной \(z,\) получаем \[ {\frac{x}{a} + \frac{y}{b} + \frac{z}{c} \le 1,}\;\; {\Rightarrow \frac{z}{c} \le 1 - \frac{x}{a} - \frac{y}{b}}\;\; {\text{или}\;\;z \le c\left( {1 - \frac{x}{a} - \frac{y}{b}} \right).} \] Вычислим тройной интеграл: \[\require{cancel} {\iiint\limits_G {dxdydz} } = {\int\limits_0^a {dx} \int\limits_0^{b\left( {1 - \large\frac{x}{a}\normalsize} \right)} {dy} \int\limits_0^{c\left( {1 - \large\frac{x}{a}\normalsize - \large\frac{y}{b}\normalsize} \right)} {dz} } = {\int\limits_0^a {dx} \int\limits_0^{b\left( {1 - \large\frac{x}{a}\normalsize} \right)} {c\left( {1 - \frac{x}{a} - \frac{y}{b}} \right)dy} } = {c\int\limits_0^a {\left[ {\left. {\left( {\left( {1 - \frac{x}{a}} \right)y - \frac{{{y^2}}}{{2b}}} \right)} \right|_{y = 0}^{b\left( {1 - \large\frac{x}{a}\normalsize} \right)}} \right]dx} } = {bc\int\limits_0^a {\left[ {\left( {1 - \frac{x}{a}} \right)\left( {1 - \frac{x}{a}} \right) - \frac{{{{\left( {1 - \frac{x}{a}} \right)}^2}}}{2}} \right]dx} } = {\frac{{bc}}{{2{a^2}}}\int\limits_0^a {{{\left( {a - x} \right)}^2}dx} } = {\frac{{bc}}{{2{a^2}}}\int\limits_0^a {\left( {{a^2} - 2ax + {x^2}} \right)dx} } = {\frac{{bc}}{{2{a^2}}}\left[ {\left. {\left( {{a^2}x - a{x^2} + \frac{{{x^3}}}{3}} \right)} \right|_0^a} \right] } = {\frac{{bc}}{{2{a^2}}}\left( {\cancel{a^3} - \cancel{a^3} + \frac{{{a^3}}}{3}} \right) } = {\frac{{abc}}{6}.} \] Соответственно, исходный интеграл равен \[ {\iint\limits_S{2xdydz + \left( {3y + x} \right)dxdy + \left( {2y + 4z} \right)dxdy} } = {9\iiint\limits_G{dxdydz} } = {9 \cdot \frac{{abc}}{6} } = {\frac{{3abc}}{2}.} \]