|
Сходимость рядов Фурье
|
|||||||||||||||
|
Некоторые определения
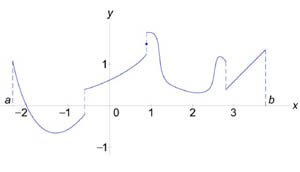
Говорят, что функция \(f\left( x \right),\) определенная в интервале \(\left[ {a,b} \right],\) является кусочно непрерывной, если она непрерывна всюду в данном интервале, за исключением конечного числа точек разрыва (рисунок \(1\)).
Частичные суммы ряда Фурье
Введем понятие частичной суммы ряда Фурье \({f_N}\left( x \right)\) функции \(f\left( x \right),\) заданной в интервале \(\left[ {-\pi, \pi} \right].\) Она определяется выражением \[{f_N}\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^N {\left( {{a_n}\cos nx + {b_n}\sin nx} \right)} .\] В комплексной форме частичная сумма \({f_N}\left( x \right)\) функции \(f\left( x \right),\) заданной в интервале \(\left[ {-\pi, \pi} \right],\) выражается формулой \[ {{f_N}\left( x \right) = \sum\limits_{n = - N}^N {{c_n}{e^{inx}}} } = {\int\limits_{ - \pi }^\pi {\left( {\frac{1}{{2\pi }}\sum\limits_{n = - N}^N {{e^{in\left( {x - y} \right)}}} } \right)f\left( y \right)dy} .} \]
Ядро Дирихле
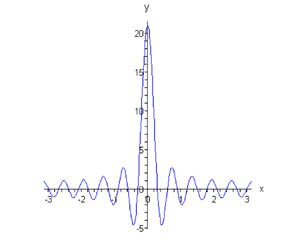
Функция \[{D_N}\left( x \right) = \sum\limits_{n = - N}^N {{e^{inx}}} = \frac{{\sin \left( {N + \frac{1}{2}} \right)x}}{{\sin \frac{x}{2}}}\] называется ядром Дирихле. На рисунке \(2\) показан вид этой функции при \(n = 10.\)Частичная сумма ряда Фурье выражается через ядро Дирихле следующим образом: \[ {{f_N}\left( x \right) = \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{D_N}\left( {x - y} \right)f\left( y \right)dy} } = {\frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{D_N}\left( y \right)f\left( {x - y} \right)dy} .} \] В данной секции мы рассмотрим три типа сходимости рядов Фурье: сходимость в точке, равномерную сходимость и сходимость в пространстве \({L_2}.\)
Сходимость ряда Фурье в точке
Пусть \(f\left( x \right)\) является кусочно гладкой функцией в интервале \(\left[ {-\pi, \pi} \right].\) Тогда для любого \({x_0} \in \left[ { - \pi ,\pi } \right]\) выполняется условие \[ \lim\limits_{N \to \infty } {f_N}\left( {{x_0}} \right) = \begin{cases} f\left( {{x_0}} \right), & \text{если}\,f\left( x \right)\,\text{непрерывна в}\, \left[ { - \pi ,\pi } \right] \\ \frac{{f\left( {{x_0} - 0} \right) + f\left( {{x_0} + 0} \right)}}{2}, & \text{если}\,f\left( x \right)\,\text{имеет разрыв при}\, {{x_0}} \end{cases}, \] где \({f\left( {{x_0} - 0} \right)}\) и \({f\left( {{x_0} + 0} \right)}\) представляют собой, соответственно, левосторонний и правосторонний пределы в точке \({x_0}.\)
Равномерная сходимость ряда Фурье
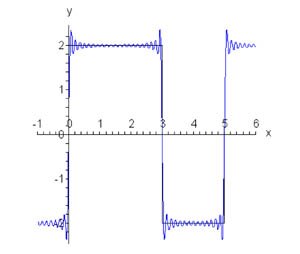
Говорят, что последовательность частичных сумм ряда Фурье \(\left\{ {{f_N}\left( x \right)} \right\}\) сходится равномерно к функции \(f\left( x \right),\) если скорость сходимости частичных сумм \({{f_N}\left( x \right)}\) не зависит от \(x.\) (рисунок \(3\)). Будем говорить, что ряд Фурье функции \(f\left( x \right)\) сходится равномерно к этой функции, если \[\lim\limits_{N \to \infty } \left[ {\max\limits_{x \in \left[ { - \pi ,\pi } \right]} \left| {f\left( x \right) - {f_N}\left( x \right)} \right|} \right] = 0.\] Теорема. Ряд Фурье \(2\pi\)-периодической непрерывной и кусочно гладкой функции сходится равномерно.
Сходимость ряда Фурье в пространстве \({L_2}\)
Пространство \({L_2}\left( { - \pi ,\pi } \right)\) образовано функциями, удовлетворяющими условию \[\int\limits_{ - \pi }^\pi {{{\left| {f\left( x \right)} \right|}^2}dx} < \infty .\] Будем говорить, что функция \(f\left( x \right)\) является квадратично интегрируемой, если она принадлежит классу \({L_2}.\) Если \(f\left( x \right)\) квадратично интегрируема, то \[\lim\limits_{N \to \infty } \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{{\left| {f\left( x \right) - {f_N}\left( x \right)} \right|}^2}dx} = 0,\] то есть частичные суммы \({f_N}\left( x \right)\) сходятся к \(f\left( x \right)\) в смысле среднего квадратичного.Из равномерной сходимости ряда Фурье следует как сходимость в точке, так и сходимость в пространстве \({L_2}.\) Обратное утверждение неверно: сходимость в пространстве \({L_2}\) не означает, что ряд Фурье сходится в точке или равномерно, и, аналогично, из сходимости в точке не вытекает равномерная сходимость или сходимость в пространстве \({L_2}.\)
Явление Гиббса
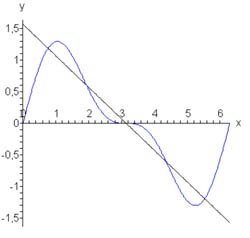
Если функция имеет разрыв второго рода в некоторой точке, то частичные суммы ряда Фурье будут осциллировать вблизи этой точки (смотрите рисунок \(4\)). Этот эффект называется феноменом или явлением Гиббса. В любой точке разрыва второго рода амплитуда выбросов примерно на \(18\%\) (при \(n \to \infty\)) превышает амплитуду скачка функции в точке разрыва. |
|||||||||||||||
|
Пример 1
|
|||||||||||||||
|
Вычислить интеграл \(\int\limits_{ - \pi }^\pi {{D_N}\left( z \right)dz} .\)
Решение. Найдем новые пределы интегрирования: если \(y = 0,\) то \(z = x\) и, соответственно, \(z = x - \pi\) при \(y = \pi.\) В результате получаем \[ {1 = \frac{1}{\pi }\int\limits_x^{x - \pi } {{D_N}\left( z \right)\left( { - dz} \right)} \;\;\text{или}}\;\; {1 = \frac{1}{\pi }\int\limits_{x - \pi}^x {{D_N}\left( z \right)dz} .} \] Вследствие периодичности \({{D_N}\left( x \right)}\) можно записать \[1 = \frac{1}{\pi }\int\limits_{ - \pi }^0 {{D_N}\left( z \right)dz} .\] Следовательно, \[\int\limits_{ - \pi }^\pi {{D_N}\left( z \right)dz} = 2\int\limits_{ - \pi }^0 {{D_N}\left( z \right)dz} = 2\pi .\] Можно предложить и другой способ вычисления данного интеграла. Перепишем его в виде \[I = \int\limits_{ - \pi }^\pi {{D_N}\left( z \right)dz} = 2\int\limits_0^\pi {{D_N}\left( z \right)dz} .\] Поскольку \[ {{D_N}\left( z \right) = \frac{{\sin \left( {N + \frac{1}{2}} \right)z}}{{\sin \frac{z}{2}}} } = {2\left( {\frac{1}{2} + \sum\limits_{n = 1}^N {\cos nz} } \right),} \] то мы можем проинтегрировать этот ряд почленно. Тогда \[ {I = 2\int\limits_0^\pi {{D_N}\left( z \right)dz} } = {4\int\limits_0^\pi {\left( {\frac{1}{2} + \sum\limits_{n = 1}^N {\cos nz} } \right)dz} } = {4\left[ {\left. {\left( {\frac{z}{2} + \sum\limits_{n = 1}^N {\frac{{\sin nz}}{n}} } \right)} \right|_0^\pi } \right].} \] Здесь \(\sin nz = 0\) при \(z = 0, \pi.\) Таким образом, \[I = 4 \cdot \frac{\pi }{2} = 2\pi .\] |
|||||||||||||||
|
Пример 2
|
|||||||||||||||
|
Пусть функция \(f\left( x \right) = \large\frac{{\pi - x}}{2}\normalsize\) определена в интервале \(\left[ {0,2\pi } \right].\) Найти разложение данной функции в ряд Фурье в указанном интервале и вывести формулу для приближенного вычисления числа \(\pi.\)
Решение. |
|||||||||||||||
|
Пример 3
|
|||||||||||||||
|
Доказать, что ряд Фурье функции \(f\left( x \right) = {x^2}\) сходится равномерно к \(f\left( x \right)\) в интервале \(\left[ {-\pi, \pi} \right].\)
Решение. Соответственно, частичные суммы определяются соотношением \[{f_N}\left( x \right) = \frac{{{\pi ^2}}}{3} + 4\sum\limits_{n = 1}^N {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} .\] Тогда справедлива оценка \[ {\left| {f\left( x \right) - {f_N}\left( x \right)} \right| } = {\left| {4\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} - 4\sum\limits_{n = 1}^N {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} } \right| } = {\left| {4\sum\limits_{n = N + 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} } \right| } \le {4\sum\limits_{n = N + 1}^\infty {\left| {\frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}}\cos nx} \right|} } \le {4\sum\limits_{n = N + 1}^\infty {\frac{1}{{{n^2}}}} .} \] Последняя сумма сходится к нулю при \(N \to \infty.\) В самом деле, применяя интегральный признак сходимости, находим, что \[ {\lim\limits_{N \to \infty } \sum\limits_{n = N + 1}^\infty {\frac{1}{{{n^2}}}} } = {\lim\limits_{N \to \infty } \int\limits_{N + 1}^\infty {\frac{{dx}}{{{x^2}}}} } = {\lim\limits_{N \to \infty } \left[ {\left. {\left( { - \frac{1}{x}} \right)} \right|_{N + 1}^\infty } \right] } = {\lim\limits_{N \to \infty } \frac{1}{{N + 1}} = 0.} \] Таким образом, \[\lim\limits_{N \to \infty } \left[ {\max\limits_{x \in \left[ { - \pi ,\pi } \right]} \left| {f\left( x \right) - {f_N}\left( x \right)} \right|} \right] = 0,\] что подразумевает равномерную сходимость ряда Фурье для функции \(f\left( x \right) = {x^2}.\) |
|||||||||||||||
|
Пример 4
|
|||||||||||||||
|
Доказать, что ряд Фурье функции \(f\left( x \right) = x,\) заданный в интервале \(\left[ {-\pi, \pi} \right],\) сходится в пространстве \({L_2}.\)
Решение. Тогда частичные суммы определяются выражением \[{f_N}\left( x \right) = 2\sum\limits_{n = 1}^N {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} .\] Вычислим предел \[ {\lim\limits_{N \to \infty } \frac{1}{{2\pi }}\int\limits_{ - \pi }^\pi {{{\left| {f\left( x \right) - {f_N}\left( x \right)} \right|}^2}dx} } = {\lim\limits_{N \to \infty } \left\| {f\left( x \right) - {f_N}\left( x \right)} \right\|,} \] где \(\left\| {f\left( x \right)} \right\|\) обозначает норму функции \({f\left( x \right)}\) в пространстве \({L_2}.\) Найдем норму \(\left\| {f\left( x \right) - {f_N}\left( x \right)} \right\|:\) \[ {\left\| {f\left( x \right) - {f_N}\left( x \right)} \right\| } = {\sqrt {\frac{1}{{2\pi }}{{\int\limits_{ - \pi }^\pi {\left| {\sum\limits_{n = 1}^\infty {\frac{{2{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} - \sum\limits_{n = 1}^N {\frac{{2{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} } \right|} }^2}dx} } = {\left\| {\sum\limits_{n = N + 1}^\infty {\frac{{2{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} } \right\|.} \] Используя неравенство треугольников \(\left\| {f + g} \right\| \le \left\| f \right\| + \left\| g \right\|\) для функций в пространстве \({L_2},\) можно записать \[ {\left\| {f\left( x \right) - {f_N}\left( x \right)} \right\| } = {\left\| {\sum\limits_{n = N + 1}^\infty {\frac{{2{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} } \right\| } \le {\sum\limits_{n = N + 1}^\infty {\left\| {\frac{{2{{\left( { - 1} \right)}^{n + 1}}}}{n}\sin nx} \right\|} } \le {\sum\limits_{n = N + 1}^\infty {\left\| {\frac{2}{n}} \right\|} } = {\lim\limits_{N \to \infty } \sum\limits_{n = N + 1}^\infty {{{\left( {\frac{2}{n}} \right)}^2}} } = {\lim\limits_{N \to \infty } \sum\limits_{n = N + 1}^\infty {\frac{4}{{{n^2}}}}. } \] Последний предел равен нулю: \[ {\lim\limits_{N \to \infty } \left\| {f\left( x \right) - {f_N}\left( x \right)} \right\| } = {\lim\limits_{N \to \infty } \sum\limits_{n = N + 1}^\infty {\frac{4}{{{n^2}}}} = 0.} \] Таким образом, доказано, что в заданном интервале ряд Фурье функции \(f\left( x \right) = x\) сходится в смысле среднеквадратичного к самой функции. |
|||||||||||||||
|
Пример 5
|
|||||||||||||||
|
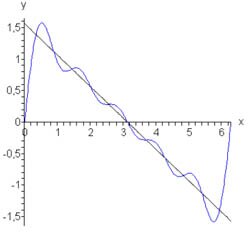
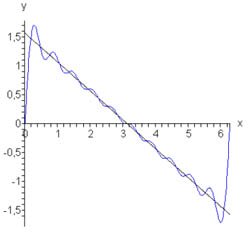
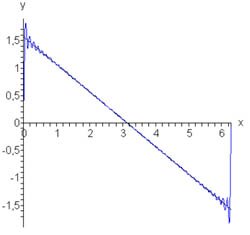
Известно, что ряд Фурье функции \(f\left( x \right) = \large\frac{{\pi - x}}{2}\normalsize,\) заданной в интервале \(\left[ {0,2\pi } \right],\) выражается формулой \(f\left( x \right) = \large\frac{{\pi - x}}{2}\normalsize = \sum\limits_{n = 1}^\infty {\large\frac{{\sin nx}}{n}\normalsize} \) (смотрите пример \(2\) выше). Исследовать поведение частичных сумм \({f_N}\left( x \right).\)
Решение.
Как видно, амплитуда выброса вследствие эффекта Гиббса составляет примерно \(18\%.\) |
|||||||||||||||