Разложение в ряд Фурье непериодических функций

Рассмотрим кусочно-непрерывную \(f\left( x \right),\) заданную в интервале \(\left[ { - L,L} \right].\) Используя подстановку \(x = \large\frac{{Ly}}{\pi }\normalsize\;\left( { - \pi \le x \le \pi } \right),\) преобразуем ее в функцию \[F\left( y \right) = f\left( {\frac{{Ly}}{\pi }} \right),\] определенную и интегрируемую в интервале \(\left[ { - \pi ,\pi } \right].\) Разложение в ряд Фурье для функции \(F\left( y \right)\) имеет вид \[ {F\left( y \right) = f\left( {\frac{{Ly}}{\pi }} \right) } = {\frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos ny + {b_n}\sin ny} \right)} .} \] Коэффициенты Фурье для данной функции определяются формулами \[{a_0} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {F\left( y \right)dy} ,\] \[ {{a_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {F\left( y \right)\cos nydy} } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( {\frac{{Ly}}{\pi }} \right)\cos nydy} ,} \] \[ {{b_n} = \frac{1}{\pi }\int\limits_{ - \pi }^\pi {F\left( y \right)\sin nydy} } = {\frac{1}{\pi }\int\limits_{ - \pi }^\pi {f\left( {\frac{{Ly}}{\pi }} \right)\sin nydy} ,}\; {n = 1,2,3, \ldots } \] Возвращаясь к первоначальным переменным, то есть полагая \(y = \large\frac{{\pi x}}{L}\normalsize,\) получим следующие выражения для ряда Фурье исходной функции \(f\left( x \right):\) \[ f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos \frac{{n\pi x}}{L} + {b_n}\sin\frac{{n\pi x}}{L}} \right)} , \] где \[ {{a_0} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} ,}\;\; {{b_n} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} .} \] Если функция \(f\left( x \right)\) определена в интервале \(\left[ { a,b} \right],\) то ее разложение в ряд Фурье определяется той же самой формулой \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos \frac{{n\pi x}}{L} + {b_n}\sin\frac{{n\pi x}}{L}} \right)} ,\] где \(L = \large\frac{{b - a}}{2}\normalsize,\) а коэффициенты вычисляются следующим образом: \[ {{a_0} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} ,}\;\; {{b_n} = \frac{1}{L}\int\limits_{ - L}^L {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} ,}\;\; {n = 1,2,3, \ldots } \] Разложение в ряд Фурье четной функции, определенной в интервале \(\left[ { - L,L} \right],\) имеет вид \[f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos \frac{{n\pi x}}{L}} ,\] где \[ {{a_0} = \frac{2}{L}\int\limits_0^L {f\left( x \right)dx} ,}\;\; {{a_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx}.} \] Разложение в ряд Фурье нечетной функции, заданной в интервале \(\left[ { - L,L} \right],\) выражается формулой \[f\left( x \right) = \sum\limits_{n = 1}^\infty {{b_n}\sin\frac{{n\pi x}}{L}} ,\] где коэффициенты Фурье равны \[{b_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} .\]

   Пример 1

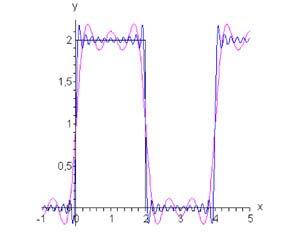
Найти разложение в ряд Фурье функции \[ f\left( x \right) = \begin{cases} A, & 0 \le x \le L \\ 0, & L < x \le 2L \end{cases}. \] Определим коэффициенты разложения: \[ {{a_0} = \frac{1}{L}\int\limits_a^b {f\left( x \right)dx} } = {\frac{1}{L}\int\limits_0^L {Adx} = A,} \] \[ {{a_n} = \frac{1}{L}\int\limits_a^b {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} } = {\frac{1}{L}\int\limits_a^b {A\cos \frac{{n\pi x}}{L}dx} } = {\frac{A}{L}\left[ {\left. {\left( {\frac{L}{{n\pi }}\sin\frac{{n\pi x}}{L}} \right)} \right|_0^L} \right] } = {\frac{A}{{n\pi }}\left( {\sin n\pi - \sin 0} \right) = 0,} \] \[ {{b_n} = \frac{1}{L}\int\limits_a^b {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} } = {\frac{1}{L}\int\limits_a^b {A\sin \frac{{n\pi x}}{L}dx} } = {\frac{A}{L}\left[ {\left. {\left( { - \frac{L}{{n\pi }}\cos\frac{{n\pi x}}{L}} \right)} \right|_0^L} \right] } = {\frac{A}{{n\pi }}\left[ { - \cos n\pi + \cos 0} \right] = \frac{A}{{n\pi }}\left[ {1 - {{\left( { - 1} \right)}^n}} \right] } = {\frac{A}{{n\pi }}\left[ {1 + {{\left( { - 1} \right)}^{n + 1}}} \right].} \] Можно заметить, что для четных \(n = 2k,\;k = 1,2,3, \ldots \) \[{b_{2k}} = \frac{A}{{2k\pi }}\left[ {1 + {{\left( { - 1} \right)}^{2k + 1}}} \right] = 0.\] Для нечетных \(n = 2k - 1,\;k = 1,2,3, \ldots \) \[ {{b_{2k - 1}} = \frac{A}{{\left( {2k - 1} \right)\pi }}\left[ {1 + {{\left( { - 1} \right)}^{2k}}} \right] } = {\frac{{2A}}{{\left( {2k - 1} \right)\pi }}.} \] Следовательно, разложение в ряд Фурье имеет вид (рисунок \(1\)) \[f\left( x \right) = \frac{A}{2} + \frac{{2A}}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{{2k - 1}}\sin \left( {\frac{{2k - 1}}{L}\pi x} \right)} .\]

   Пример 2

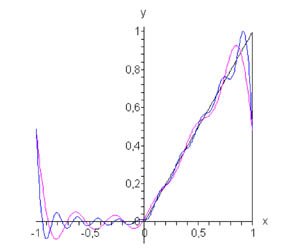
Найти разложение в ряд Фурье функции: \[ f\left( x \right) = \begin{cases} 0, & -1 \le x \le 0 \\ x, & 0 < x \le 1 \end{cases}. \] Здесь \(L = 1.\) Следовательно, можно записать \[ {{a_0} = \frac{1}{L}\int\limits_a^b {f\left( x \right)dx} } = {\int\limits_{ - 1}^1 {f\left( x \right)dx} } = {\int\limits_0^1 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^1 = \frac{1}{2}.} \] Вычислим коэффициенты \({a_n}:\) \[ {{a_n} = \frac{1}{L}\int\limits_a^b {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} } = {\int\limits_0^1 {x\cos \left( {n\pi x} \right)dx} } = {\left. {\left( {\frac{1}{{n\pi }}x\sin \left( {n\pi x} \right)} \right)} \right|_0^1 - \frac{1}{{n\pi }}\int\limits_0^1 {\sin \left( {n\pi x} \right)dx} } = {\frac{1}{{n\pi }}\left[ {\left. {\left( {x\sin n\pi x} \right)} \right|_0^1 + \left. {\left( {\frac{{\cos n\pi x}}{{n\pi }}} \right)} \right|_0^1} \right] } = {\frac{1}{{n\pi }}\left[ {\sin n\pi + \frac{{\cos n\pi }}{{n\pi }} - \frac{1}{{n\pi }}} \right] } = {\frac{1}{{{n^2}{\pi ^2}}}\left[ {\cos n\pi - 1} \right] } = {\frac{1}{{{n^2}{\pi ^2}}}\left[ {{{\left( { - 1} \right)}^n} - 1} \right].} \] Определим теперь коэффициенты \({b_n}:\) \[ {{b_n} = \frac{1}{L}\int\limits_a^b {f\left( x \right)\sin\frac{{n\pi x}}{L}dx} } = {\int\limits_0^1 {x\sin \left( {n\pi x} \right)dx} } = {\left. {\left( { - \frac{1}{{n\pi }}x\cos \left( {n\pi x} \right)} \right)} \right|_0^1 + \frac{1}{{n\pi }}\int\limits_0^1 {\cos\left( {n\pi x} \right)dx} } = {\frac{1}{{n\pi }}\left[ {\left. { - \left( {x\cos n\pi x} \right)} \right|_0^1 + \left. {\left( {\frac{{\sin n\pi x}}{{n\pi }}} \right)} \right|_0^1} \right] } = {\frac{1}{{n\pi }}\left[ { - \cos n\pi + \frac{{\sin n\pi }}{{n\pi }}} \right] } = {\frac{{{{\left( { - 1} \right)}^{n + 1}}}}{{n\pi }}.} \] В результате получаем следующее выражение для ряда Фурье (рисунок \(2\)): \[ {f\left( x \right) = \frac{1}{4} } + {\sum\limits_{n = 1}^\infty {\left[ {\frac{{\left( {{{\left( { - 1} \right)}^n} - 1} \right)}}{{{n^2}{\pi ^2}}}\cos n\pi x + \frac{{{{\left( { - 1} \right)}^{n + 1}}}}{{n\pi }}\sin n\pi x} \right]} .} \]

   Пример 3

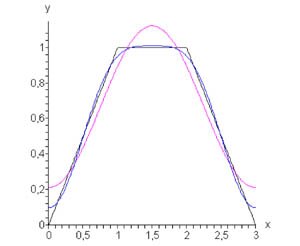
Найти разложение в ряд Фурье трапециевидной волны, заданной функцией \[ f\left( x \right) = \begin{cases} x, & 0 \le x \le 1 \\ 1, & 1 \lt x \le 2 \\ 3-x, & 2 \lt x \le 3 \end{cases}. \] В данном случае, очевидно, \(L = \large\frac{3}{2}\normalsize.\) Вычислим коэффициенты разложения \({a_0}\) и \({a_n}.\) \[ {{a_0} = \frac{1}{L}\int\limits_a^b {f\left( x \right)dx} } = {\frac{2}{3}\int\limits_0^3 {f\left( x \right)dx} } = {\frac{2}{3}\left[ {\int\limits_0^1 {xdx} + \int\limits_1^2 {1dx} + \int\limits_2^3 {\left( {3 - x} \right)dx} } \right] } = {\frac{2}{3}\left[ {\left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^1 + \left. x \right|_0^1 + \left. {\left( {3x - \frac{{{x^2}}}{2}} \right)} \right|_2^3} \right] } = {\frac{4}{3};} \] \[ {{a_n} = \frac{1}{L}\int\limits_a^b {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} } = {\frac{2}{3}\int\limits_0^3 {f\left( x \right)\cos \frac{{2n\pi x}}{3}dx} } = {\frac{2}{3}\left\{ {\int\limits_0^1 {x\cos \frac{{2n\pi x}}{3}dx} } \right. } + {\int\limits_1^2 {\cos \frac{{2n\pi x}}{3}dx} } + {\left. {\int\limits_2^3 {\left( {3 - x} \right)\cos \frac{{2n\pi x}}{3}dx} } \right\} } = {\frac{2}{3}\left\{ {\left[ {\left. {\left( {\frac{3}{{2n\pi }}x\sin\frac{{2n\pi x}}{3}} \right)} \right|_0^1 - \int\limits_0^1 {\frac{3}{{2n\pi }}\sin\frac{{2n\pi x}}{3}dx} } \right]} \right. } + {\left. {\left( {\frac{3}{{2n\pi }}\sin\frac{{2n\pi x}}{3}} \right)} \right|_1^2 } + {\left. {\left[ {\left. {\left( {\frac{3}{{2n\pi }}\left( {3 - x} \right)\sin\frac{{2n\pi x}}{3}} \right)} \right|_2^3 + \int\limits_2^3 {\frac{3}{{2n\pi }}\sin\frac{{2n\pi x}}{3}dx} } \right]} \right\} } = {\frac{2}{3}\left\{ {\frac{3}{{2n\pi }}\sin\frac{{2n\pi }}{3}} \right. } + {\frac{9}{{4{n^2}{\pi ^2}}}\left( {\cos\frac{{2n\pi }}{3} - 1} \right) } + {\frac{3}{{2n\pi }}\left( {\sin\frac{{4n\pi }}{3} - \sin\frac{{2n\pi }}{3}} \right) } - {\frac{3}{{2n\pi }}\sin\frac{{4n\pi }}{3} } + {\left. {\frac{9}{{4{n^2}{\pi ^2}}}\left( { - \cos 2n\pi + \cos\frac{{4n\pi }}{3}} \right)} \right\} } = {\frac{2}{3}\left\{ {\frac{9}{{4{n^2}{\pi ^2}}}\left( {\cos\frac{{2n\pi }}{3} - 1} \right) + \frac{9}{{4{n^2}{\pi ^2}}}\left( {\cos\frac{{4n\pi }}{3} - 1} \right)} \right\}.} \] Так как \(\cos \large\frac{{4n\pi }}{3}\normalsize = \cos \left( {2n\pi - \large\frac{{2n\pi }}{3}\normalsize} \right) = \cos \large\frac{{2n\pi }}{3}\normalsize,\) то получаем \[ {{a_n} = \frac{2}{3} \cdot \frac{{2 \cdot 9}}{{4{n^2}{\pi ^2}}}\left( {\cos \frac{{2n\pi }}{3} - 1} \right) } = {\frac{3}{{{n^2}{\pi ^2}}}\left( {\cos \frac{{2n\pi }}{3} - 1} \right),}\; {n = 1,2,3, \ldots } \] Коэффициенты \({b_n}\) равны нулю, поскольку функция четная на заданном интервале \(\left[ {0,3} \right].\) Тогда разложение в ряд Фурье выражается формулой \[f\left( x \right) = \frac{2}{3} - \frac{3}{{{\pi ^2}}}\sum\limits_{n = 1}^\infty {\frac{{1 - \cos \frac{{2n\pi }}{3}}}{{{n^2}}}\cos \frac{{2n\pi x}}{3}} .\] График данной функции и аппроксимации Фурье при \(n = 1\) и \(n = 3\) показаны на рисунке \(3.\)

   Пример 4

Найти разложение в ряд Фурье функции \(f\left( x \right) = {\cos ^2}x.\) Данная функция − четная и имеет период \(\pi\) \(\left( {L = \large\frac{\pi }{2}\normalsize} \right).\) Поэтому \({b_n} = 0.\) Определим коэффициенты \({a_0}\) и \({a_n}.\) \[ {{a_0} = \frac{2}{L}\int\limits_0^L {f\left( x \right)dx} } = {\frac{4}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}xdx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 + \cos 2x} \right)dx} } = {\frac{2}{\pi }\left[ {\left. {\left( {x + \frac{{\sin 2x}}{2}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{2}{\pi }\left[ {\frac{\pi }{2} + \frac{{\sin \pi }}{2}} \right] = 1.} \] \[ {{a_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx} } = {\frac{4}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}x\cos 2nxdx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 + \cos 2x} \right)\cos 2nxdx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\cos 2nx + \cos 2x\cos 2nx} \right)dx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left\{ {\cos 2nx + \frac{1}{2}\left[ {\cos \left( {2n - 2} \right)x + \cos \left( {2n + 2} \right)x} \right]} \right\}dx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left[ {2\cos 2nx + \cos \left( {2n - 2} \right)x + \cos \left( {2n + 2} \right)x} \right]dx} } = {\frac{1}{\pi }\left. {\left[ {\sin \frac{{2nx}}{n} + \sin \frac{{\left( {2n - 2} \right)x}}{{2n - 2}} + \sin \frac{{\left( {2n + 2} \right)x}}{{2n + 2}}} \right]} \right|_0^{\large\frac{\pi }{2}\normalsize} } = {\frac{1}{\pi }\left[ {\frac{{\sin n\pi }}{n} + \frac{{\sin \left( {n - 1} \right)\pi }}{{2n - 2}} + \frac{{\sin \left( {n + 1} \right)\pi }}{{2n + 2}}} \right] = 0.} \] Однако полученный результат справедлив лишь при \(n \ge 2.\) Поэтому рассчитаем \({a_1}\) отдельно. \[ {{a_1} = \frac{4}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}x\cos 2xdx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {1 + \cos 2x} \right)\cos 2xdx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\cos 2x + {{\cos }^2}2x} \right)dx} } = {\frac{2}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\cos 2x + \frac{{1 + \cos 4x}}{2}} \right)dx} } = {\frac{1}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {2\cos 2x + 1 + \cos 4x} \right)dx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\sin 2x + x + \frac{{\sin 4x}}{4}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{1}{\pi }\left( {\sin \pi + \frac{\pi }{2} + \frac{{\sin 2\pi }}{4}} \right) } = {\frac{1}{2}.} \] Таким образом, разложение в ряд Фурье функции \(f\left( x \right) = {\cos ^2}x\) имеет вид \[f\left( x \right) = {\cos ^2}x = \frac{1}{2} + \frac{1}{2}\cos 2x.\] Полученное выражение является хорошо известным тригонометрическим тождеством.