Производная функции в полярных координатах

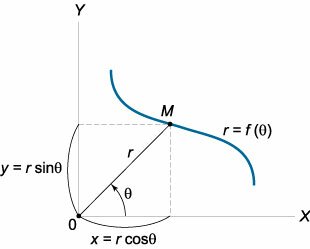
Положение точек на плоскости можно описывать в различных системах координат. Помимо прямоугольной декартовой системы координат широко распространена также полярная система координат. В ней положение любой точки \(M\) описывается двумя числами (рис.\(1\)):

• длиной радиус-вектора \(r\), равной расстоянию от точки \(M\) до центра координат \(O\) (полюса);


• полярным углом \(\theta\), образованным отрезком \(OM\) и положительным направлением оси \(Ox\). Угол \(\theta\) отсчитывается против часовой стрелки.

Равенство \(r = f\left( \theta \right)\), выражающее зависимость длины радиус-вектора \(r\) от полярного угла \(\theta\), описывает на плоскости некоторую кривую и называется полярным уравнением кривой.

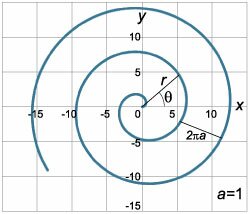
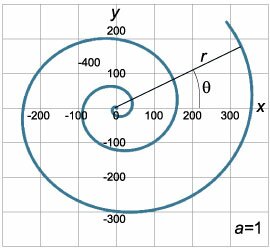
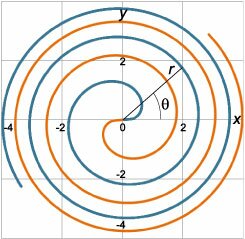
Например, Архимедова спираль (рис.\(2\)) описывается полярным уравнением \[r = a\theta ,\] где \(a\) − параметр, определяющий плотность витков спирали. Шаг спирали (расстояние между соседними витками) является для спирали Архимеда постоянной величиной, равной \(2\pi a\).

Переход от полярных координат \(\left( {r,\theta } \right)\) к прямоугольным декартовым координатам \(\left( {x,y} \right)\) производится по формулам \[x = r\cos \theta ,\;\;y = r\sin \theta .\] Если некоторая кривая задана полярным уравнением \(r = f\left( \theta \right)\), то в декартовых координатах она будет описываться системой уравнений \[ \left\{ \begin{aligned} x &= f\left( \theta \right)\cos\theta \\ y &= f\left( \theta \right)\sin\theta \end{aligned} \right., \] Видно, что фактически мы получили параметрические уравнения кривой, где роль параметра \(t\) играет \(\theta\). В таком случае производную полярной кривой можно найти по формуле производной параметрически заданной функции \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{{{\left( {f\left( \theta \right)\sin \theta } \right)}^\prime }}}{{{{\left( {f\left( \theta \right)\cos\theta } \right)}^\prime }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin \theta }}.} \] Рассмотрим примеры вычисления производных для некоторых полярных кривых.

   Пример 1

Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) Архимедовой спирали. Уравнение Архимедовой спирали (рис.\(2\)) в полярных координатах записывается в виде \[r = f\left( \theta \right) = a\theta .\] Производная \(\large\frac{{dy}}{{dx}}\normalsize\) находится по формуле \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin \theta }}.} \] Подставляя функцию \(f\left( \theta \right)\), имеем \[ {\frac{{dy}}{{dx}} = \frac{{{{\left( {a\theta } \right)}^\prime }\sin \theta + a\theta \cos\theta }}{{{{\left( {a\theta } \right)}^\prime }\cos\theta - a\theta \sin \theta }} } = {\frac{{a\sin \theta + a\theta \cos \theta }}{{a\cos \theta - a\theta \sin \theta }} } = {\frac{{\sin \theta + \theta \cos \theta }}{{\cos \theta - \theta \sin \theta }}.} \] Разделим числитель и знаменатель на \({\cos \theta }\) (полагая, что \(\theta \ne \large\frac{\pi }{2}\normalsize + \pi n,\;n \in \mathbb{Z}\)). Тогда для производной получается такое выражение: \[\frac{{dy}}{{dx}} = \frac{{\tan\theta + \theta }}{{1 - \theta \tan \theta }}.\] Последнюю формулу можно еще упростить, если воспользоваться тригонометрическим соотношением \[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\] Для этого представим угол \(\theta\) как \[\theta = \tan \left( {\arctan\theta } \right).\] В результате получаем \[ {\frac{{dy}}{{dx}} = \frac{{\tan\theta + \theta }}{{1 - \theta \tan \theta }} } = {\frac{{\tan\theta + \tan \left( {\arctan\theta } \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan\theta } \right)}} } = {\tan \left( {\theta + \arctan\theta } \right).} \] Интересно, что производная спирали Архимеда не зависит от длины радиуса \(r\), а определяется только углом \(\theta\). В этом проявляется свойство самоподобия архимедовой спирали. Данная особенность свойственна и многим другим плоским кривым.

   Пример 2

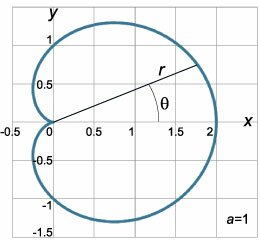
Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) кардиоиды, заданной уравнением \[r = f\left( \theta \right) = a\left( {1 + \cos \theta } \right).\] Предварительно вычислим производную полярной функции: \[ {f'\left( \theta \right) = {\left( {a\left( {1 + \cos \theta } \right)} \right)^\prime } } = { - a\sin \theta .} \] Тогда производная \(\large\frac{{dy}}{{dx}}\normalsize\) данной кривой равна \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)cos\theta }}{{f'\left( \theta \right)cos\theta - f\left( \theta \right)sin\theta }} } = {\frac{{\left( { - a\sin \theta } \right)\sin \theta + a\left( {1 + \cos \theta } \right)cos\theta }}{{\left( { - a\sin \theta } \right)cos\theta - a\left( {1 + \cos \theta } \right)sin\theta }} } = {\frac{{ - {{\sin }^2}\theta + \cos \theta + {{\cos }^2}\theta }}{{ - \sin \theta \cos \theta - \sin \theta - \sin \theta \cos \theta }}.} \] Используя формулы двойного угла \[ {\cos 2\theta = {\cos ^2}\theta - {\sin ^2}\theta ,}\;\; {\sin 2\theta = 2\sin \theta \cos \theta ,} \] получаем \[\frac{{dy}}{{dx}} = - \frac{{\cos 2\theta + \cos \theta }}{{\sin 2\theta + \sin \theta }}.\] Далее преобразуем выражение для производной с помощью тригонометрических соотношений \[ {\cos \alpha + \cos \beta = 2\cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2},}\;\; {\sin \alpha + \sin \beta = 2\sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}.} \] В результате имеем: \[\require{cancel} {\frac{{dy}}{{dx}} = - \frac{{\cos 2\theta + \cos \theta }}{{\sin 2\theta + \sin \theta }} } = { - \frac{{2\cos \frac{{2\theta + \theta }}{2}\cos \frac{{2\theta - \theta }}{2}}}{{2\sin \frac{{2\theta + \theta }}{2}\cos \frac{{2\theta - \theta }}{2}}} } = { - \frac{{\cos \frac{{3\theta }}{2}\cancel{\cos \frac{\theta }{2}}}}{{\sin \frac{{3\theta }}{2}\cancel{\cos \frac{\theta }{2}}}} } = { - \cot \frac{{3\theta }}{2}.} \] Производная \(\large\frac{{dy}}{{dx}}\normalsize\) определена при условиях \[ {\left\{ \begin{array}{l} \cos\frac{\theta }{2} \ne 0\\ \sin \frac{{3\theta }}{2} \ne 0 \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} \frac{\theta }{2} \ne \frac{\pi }{2} + \pi n\\ \frac{{3\theta }}{2} \ne \pi k \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} \theta \ne \pi + 2\pi n,\;n \in \mathbb{Z}\\ \theta \ne \frac{2}{3}\pi k,\;k \in \mathbb{Z} \end{array} \right..} \] В интервале \(\left( {-\pi,\pi} \right)\) эти ограничения соответствуют значениям \(\theta = - \pi , - \frac{{2\pi }}{3},0,\frac{{2\pi }}{3},\pi .\) В указанных точках производная кардиоиды не существует.

Кривая кардиоиды (рис.\(3\)) напоминает изображение сердца (отсюда происходит ее название) и обладает рядом замечательных свойств. Красивые математические объекты и структуры одного и того же типа часто возникают в различных областях, которые на первый взгляд совершенно не связаны друг с другом. Такие примеры вновь заставляют нас задумываться об удивительном единстве окружающего мира и природы. Так, кардиоида совершенно неожиданно появляется в знаменитом фрактальном множестве Мандельброта, занимая его центральную часть (рис.\(4\)).

   Пример 3

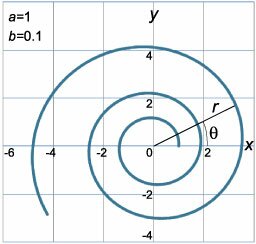
Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) логарифмической спирали, заданной уравнением \[r = f\left( \theta \right) = a{e^{b\theta }},\] где \(a\), \(b\) − действительные числа. Вычислим производную \(f'\left( \theta \right)\): \[f'\left( \theta \right) = {\left( {a{e^{b\theta }}} \right)^\prime } = ab{e^{b\theta }}.\] Подставляя это в формулу для производной \(\large\frac{{dy}}{{dx}}\normalsize\), получаем: \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} } = {\frac{{{{\left( {a{e^{b\theta }}} \right)}^\prime }\sin \theta + a{e^{b\theta }}\cos\theta }}{{{{\left( {a{e^{b\theta }}} \right)}^\prime }\cos\theta - a{e^{b\theta }}\sin\theta }} } = {\frac{{ab{e^{b\theta }}\sin \theta + a{e^{b\theta }}\cos\theta }}{{ab{e^{b\theta }}\cos\theta - a{e^{b\theta }}\sin\theta }} } = {\frac{{b\sin \theta + \cos\theta }}{{b\cos\theta - \sin\theta }} } = {\frac{{b\tan \theta + 1}}{{b - \tan \theta }} } = {\frac{{\tan \theta + \frac{1}{b}}}{{1 - \tan \theta \cdot \frac{1}{b}}}.} \] Далее, также как и в примере \(1\), представим \({\large\frac{1}{b}\normalsize}\) в виде \[\frac{1}{b} = \tan \left( {\arctan \frac{1}{b}} \right)\] и применим тригонометрическую формулу тангенса суммы двух углов: \[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\] В результате получаем: \[ {\frac{{dy}}{{dx}} = \frac{{\tan \theta + \frac{1}{b}}}{{1 - \tan \theta \cdot \frac{1}{b}}} } = {\frac{{\tan \theta + \tan \left( {\arctan \frac{1}{b}} \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan \frac{1}{b}} \right)}} } = {\tan \left( {\theta + \arctan \frac{1}{b}} \right).} \] Вид логарифмической спирали схематически представлен на рисунке \(5\). Такая форма часто встречается в природе. Например, раковины моллюсков могут иметь форму логарифмической спирали. Другой пример относится к спиральным галактикам (рис.\(6\)), для которых такая форма является типичной.

   Пример 4

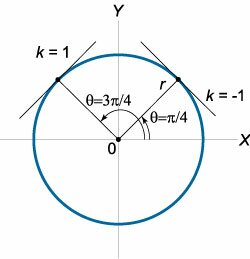
Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) окружности и вычислить ее значения для полярных углов \(\theta = \large\frac{\pi }{4}\normalsize,\large\frac{{3\pi }}{4}\normalsize.\) Уравнение окружности в полярных координатах имеет очень простой вид: \[r = f\left( \theta \right) = R,\] где \(R\) − радиус окружности.

Отсюда, учитывая, что \(f'\left( \theta \right) = 0\), легко находится производная \(\large\frac{{dy}}{{dx}}\normalsize\) окружности: \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} } = {\frac{{0 \cdot \sin \theta + R\cos\theta }}{{0 \cdot \cos\theta - R\sin\theta }} } = { - \cot \theta .} \] В частности, для углов \(\large\frac{\pi }{4}\normalsize\) и \(\large\frac{3\pi }{4}\normalsize\) производная равна: \[ {\frac{{dy}}{{dx}}\left( {\theta = \frac{\pi }{4}} \right) = - \cot\frac{\pi }{4} = - 1,}\;\; {\frac{{dy}}{{dx}}\left( {\theta = \frac{{3\pi }}{4}} \right) = - \cot\frac{{3\pi }}{4} = 1.} \] Как известно, значение производной в некоторой точке равно угловому коэффициенту (тангенсу угла наклона) касательной, проведенной к кривой в этой точке. Для указанных двух углов это схематически показано на рисунке \(7\).

   Пример 5

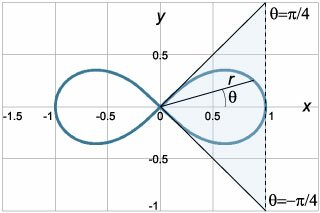
Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) лемнискаты Бернулли, заданной уравнением \[{r^2} = \cos 2\theta .\] Будем рассматривать данную кривую в интервале углов, при котором \[\cos 2\theta > 0.\] Решая это неравенство, получаем: \[ {\cos 2\theta > 0,}\;\; {\Rightarrow - \frac{\pi }{2} + 2\pi n < 2\theta < \frac{\pi }{2} + 2\pi n,}\;\; {\Rightarrow - \frac{\pi }{4} + \pi n < \theta < \frac{\pi }{4} + \pi n,\;n \in \mathbb{Z}.} \] Выберем ограниченный интервал \( - \large\frac{\pi }{4}\normalsize < \theta < \large\frac{\pi }{4}\normalsize,\) соответствующий одному лепестку лемнискаты Бернулли (рис.\(8\)). В указанном промежутке уравнение кривой можно записать в виде \[r = f\left( \theta \right) = \sqrt {\cos 2\theta } .\] Производная этой функции равна \[ {f'\left( \theta \right) = {\left( {\sqrt {\cos 2\theta } } \right)^\prime } } = {\frac{1}{{2\sqrt {\cos 2\theta } }} \cdot {\left( {\cos 2\theta } \right)^\prime } } = {\frac{1}{{2\sqrt {\cos 2\theta } }} \cdot \left( { - \sin 2\theta } \right) \cdot 2 } = { - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}.} \] Тогда производная \(\large\frac{{dy}}{{dx}}\normalsize\) будет описываться следующим выражением: \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} } = {\frac{{\left( { - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\sin \theta + \sqrt {\cos 2\theta } \cos\theta }}{{\left( { - \frac{{\sin 2\theta }}{{\sqrt {\cos 2\theta } }}} \right)\cos\theta - \sqrt {\cos 2\theta } \sin\theta }} } = { - \frac{{\frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}}{{\frac{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}{{\cancel{\sqrt {\cos 2\theta }} }}}} } = { - \frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }}.} \] Числитель и знаменатель можно упростить, используя тригонометрические соотношения для косинуса и синуса суммы двух углов: \[ {\cos\left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta ,}\;\; {\sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta.} \] Следовательно, \[ {\frac{{dy}}{{dx}} = - \frac{{\cos 2\theta \cos \theta - \sin 2\theta \sin \theta }}{{\sin 2\theta \cos \theta + \cos 2\theta \sin \theta }} } = { - \frac{{\cos \left( {2\theta + \theta } \right)}}{{\sin \left( {2\theta + \theta } \right)}} } = { - \frac{{\cos 3\theta }}{{\sin 3\theta }} = - \cot 3\theta .} \] Заметим, что функция \(\cot 3\theta \) не определена в точках, где \[ {3\theta = \pi n,}\;\; {\Rightarrow \theta = \frac{{\pi n}}{3}},\;n \in \mathbb{Z}\;\; {\text{или}\;\;\theta = 0, \pm \frac{\pi }{3}, \pm \frac{{2\pi }}{3}, \ldots} \] В наш интервал \(\left( { - \large\frac{\pi }{4}\normalsize,\large\frac{\pi }{4}\normalsize} \right)\) попадает лишь одно значение \(\theta = 0.\) В ней производная терпит бесконечный разрыв. Касательная к кривой в этой точке является вертикальной прямой (рис.\(8\)).

   Пример 6

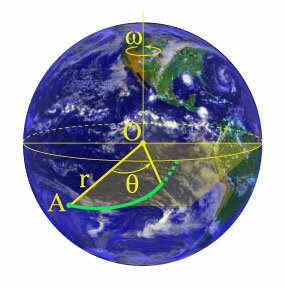
Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) спирали Галилея. Спираль Галилея описывает траекторию свободно падающего тела в системе координат, учитывающей вращение Земли. Выведем ее уравнение в полярных координатах.

Пусть тело начинает падать из некоторой точки \(A\), расположенной над экватором Земли (рис.\(9\)). Движение вдоль радиус-вектора \(r\) является равноускоренным и определяется соотношением \[r = H + R - \frac{{g{t^2}}}{2},\] где \(H\) − начальная высота тела над уровнем Земли, \(R\) − радиус Земли, \(g\) − ускорение свободного падения, \(t\) − время. Одновременно с падением тела происходит вращение Земли с постоянной угловой скоростью \(\omega\). В таком случае угол поворота \(\theta\) изменяется со временем по закону \[\theta = \omega t = \frac{{2\pi }}{T}t,\] где \(\omega\) − угловая скорость вращения Земли, \(T\) − период вращения (\(T = 24\;\text{часа} = 86400\;\text{сек}\)).

Таким образом, параметрические уравнения кривой имеют вид: \[\left\{ \begin{array}{l} r = H + R - \frac{{g{t^2}}}{2}\\ \theta = \frac{{2\pi }}{T}t \end{array} \right..\] Исключая параметр \(t\), получим полярное уравнение данной траектории: \[ {t = \frac{T}{{2\pi }}\theta ,}\;\; {\Rightarrow r = H + R - \frac{g}{2}{\left( {\frac{T}{{2\pi }}\theta } \right)^2} } = {H + R - \frac{{g{T^2}}}{{8{\pi ^2}}}{\theta ^2}.} \] Это уравнение удобнее записать в такой форме: \[ {r\left( \theta \right) = a{\theta ^2} - d,}\;\; {\text{где}\;\;a = - \frac{{g{T^2}}}{{8{\pi ^2}}},}\;\; {d = - \left( {H + R} \right).} \] Данное уравнение называется полярным уравнением спирали Галилея. В рассмотренной модели один виток спирали соответствует одному обороту Земли. Ясно, что при реальных временах падения траектория тела описывается достаточно коротким участком спирали.

Акцентируя внимание на переменном (квадратичном) члене \(a{\theta ^2}\), рассмотрим далее случай \(d = 0.\) Тогда уравнение спирали принимает следующий вид: \[r = f\left( \theta \right) = a{\theta ^2}.\] Как видно на рисунке \(10\), спираль Галилея похожа на спираль Архимеда, но отличается от нее тем, что с увеличением угла длина радиус-вектора возрастает гораздо быстрее - в соответствии с квадратичным законом. По такому же закону возрастает и шаг спирали Галилея.

Определим производную найденной полярной функции: \[ {r'\left( \theta \right) = f'\left( \theta \right) } = {{\left( {a{\theta ^2}} \right)^\prime } = 2a\theta .} \] Подставляя это в формулу для \(\large\frac{{dy}}{{dx}}\normalsize\), получаем \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos\theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} } = {\frac{{2a\theta \sin \theta + a{\theta ^2}\cos\theta }}{{2a\theta \cos\theta - a{\theta ^2}\sin\theta }} } = {\frac{{\cancel{a\theta} \left( {2\sin \theta + \theta \cos\theta } \right)}}{{\cancel{a\theta} \left( {2\cos\theta - \theta \sin\theta } \right)}} } = {\frac{{2\tan\theta + \theta }}{{2 - \theta \tan \theta }} } = {\frac{{2\tan\theta + 2 \cdot \frac{\theta }{2}}}{{2 - 2 \cdot \frac{\theta }{2} \cdot \tan \theta }} } = {\frac{{\cancel{2}\left( {\tan\theta + \frac{\theta }{2}} \right)}}{{\cancel{2}\left( {1 - \tan \theta \cdot \frac{\theta }{2}} \right)}} } = {\frac{{\tan\theta + \frac{\theta }{2}}}{{1 - \tan \theta \cdot \frac{\theta }{2}}}.} \] Снова, как и в задаче \(1\), представим угол \({\large\frac{\theta }{2}\normalsize}\) в виде \[\frac{\theta }{2} = \tan \left( {\arctan \frac{\theta }{2}} \right)\] и применим формулу тангенса суммы двух углов: \[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\] В результате находим окончательное выражение для производной \(\large\frac{{dy}}{{dx}}\normalsize\) спирали Галилея: \[ {\frac{{dy}}{{dx}} = \frac{{\tan \theta + \frac{\theta }{2}}}{{1 - \tan \theta \cdot \frac{\theta }{2}}} } = {\frac{{\tan \theta + \tan \left( {\arctan \frac{\theta }{2}} \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan \frac{\theta }{2}} \right)}} } = {\tan \left( {\theta + \arctan \frac{\theta }{2}} \right).} \]

   Пример 7

Найти производную \(\large\frac{{dy}}{{dx}}\normalsize\) спирали Ферма, заданной полярным уравнением \[r = \sqrt \theta.\] В спирали Ферма радиус \(r\) с увеличением угла \(\theta\) возрастает по корневому закону, т.е. достаточно медленно. Плотность витков увеличивается с ростом \(r\), как видно на рисунке \(11\). Такой тип спиралей также встречается в природе. Например, семена в подсолнечнике размещаются вдоль кривых, напоминающих спираль Ферма (рис.\(12\)). Возвращаясь к теме задачи, вычислим производную \(\large\frac{{dy}}{{dx}}\normalsize\) заданной кривой.

Находим сначала производную \(f'\left( \theta \right)\) в полярных координатах: \[r'\left( \theta \right) = f'\left( \theta \right) = \frac{1}{{2\sqrt \theta }}.\] Следовательно, производная в прямоугольных декартовых координатах выражается следующей формулой: \[ {\frac{{dy}}{{dx}} = {y'_x} = \frac{{{y'_\theta }}}{{{x'_\theta }}} } = {\frac{{f'\left( \theta \right)\sin \theta + f\left( \theta \right)\cos \theta }}{{f'\left( \theta \right)\cos\theta - f\left( \theta \right)\sin\theta }} } = {\frac{{\frac{1}{{2\sqrt \theta }}\sin \theta + \sqrt \theta \cos \theta }}{{\frac{1}{{2\sqrt \theta }}\cos\theta - \sqrt \theta \sin\theta }} = \frac{{\frac{{\sin \theta + 2\theta \cos \theta }}{{\cancel{2\sqrt \theta} }}}}{{\frac{{\cos\theta - 2\theta \sin \theta }}{{\cancel{2\sqrt \theta} }}}} } = {\frac{{\sin \theta + 2\theta \cos \theta }}{{\cos\theta - 2\theta \sin \theta }} } = {\frac{{\tan \theta + 2\theta }}{{1 - 2\theta \tan \theta }}.} \] Представим здесь угол \(2\theta\) как \[2\theta = \tan\left( {\arctan 2\theta } \right)\] и применим формулу тангенса суммы двух углов: \[\tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \cdot \tan \beta }}.\] Тогда производная \(\large\frac{{dy}}{{dx}}\normalsize\) принимает следующий простой вид: \[ {\frac{{dy}}{{dx}} = \frac{{\tan \theta + 2\theta }}{{1 - 2\theta \tan \theta }} } = {\frac{{\tan \theta + \tan \left( {\arctan 2\theta } \right)}}{{1 - \tan \theta \cdot \tan \left( {\arctan 2\theta } \right)}} } = {\tan \left( {\theta + \arctan 2\theta } \right).} \]