|
Положения равновесия линейных автономных систем
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Основные типы точек равновесия
Пусть задана линейная однородная система второго порядка с постоянными коэффициентами: \[\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = {a_{11}}x + {a_{12}}y\\ \frac{{dy}}{{dt}} = {a_{21}}x + {a_{22}}y \end{array} \right..\] Данная система уравнений является автономной, поскольку правые части уравнений не содержат в явном виде независимой переменной \(t.\)В матричной форме система уравнений записывается как \[ {\mathbf{X'} = A\mathbf{X},\;\;\text{где}\;\;\mathbf{X} = \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right),}\;\; {A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right).} \] Положения равновесия находятся из решения стационарного уравнения \[A\mathbf{X} = \mathbf{0}.\] Это уравнение имеет единственное решение \(\mathbf{X} = \mathbf{0},\) если матрица \(A\) является невырожденной, т.е. при условии \(\det A \ne 0.\) В случае вырожденной матрицы система имеет бесконечное множество точек равновесия. Классификация положений равновесия определяется собственными значениями \({\lambda _1},{\lambda _2}\) матрицы \(A.\) Числа \({\lambda _1},{\lambda _2}\) находятся из решения характеристического уравнения \[{\lambda ^2} - \left( {{a_{11}} + {a_{22}}} \right)\lambda + {a_{11}}{a_{22}} - {a_{12}}{a_{21}} = 0.\] В общем случае, когда матрица \(A\) является невырожденной, существует \(4\) различных типа точек равновесия:
Если действительная часть хотя бы одного собственного числа положительна, то соответствующее положение равновесия является неустойчивым. Например, это может быть седло. Наконец, в случае чисто мнимых корней (точка равновесия является центром) мы имеем дело с классической устойчивостью в смысле Ляпунова. Наша дальнейшая цель состоит в том, чтобы изучить поведение решений вблизи положений равновесия. Для систем \(2\)-го порядка это удобно делать графически с помощью фазового портрета, представляющего собой совокупность фазовых траекторий на координатной плоскости. Стрелки на фазовых траекториях показывают направление перемещения точки (т.е. некоторого конкретного состояния системы) с течением времени. Рассмотрим подробнее каждый тип точки равновесия и соответствующие фазовые портреты.
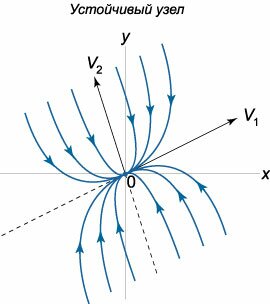
Устойчивый и неустойчивый узел
Собственные значения \({{\lambda _1},{\lambda _2}}\) точек типа "узел" удовлетворяют условиям: \[{\lambda _1},{\lambda _2} \in \Re,\;\;{\lambda _1} \cdot {\lambda _2} > 0.\] Здесь могут возникнуть следующие частные случаи.Корни \({{\lambda _1},{\lambda _2}}\) различны \(\left( {{\lambda _1} \ne {\lambda _2}} \right)\) и отрицательны \(\left( {{\lambda _1} < 0, {\lambda _2}} < 0\right).\) Построим схематический фазовый портрет такой точки равновесия. Пусть для определенности \(\left| {{\lambda _1}} \right| < \left| {{\lambda _2}} \right|.\) Общее решение системы имеет вид \[\mathbf{X}\left( t \right) = {C_1}{e^{{\lambda _1}t}}{\mathbf{V}_1} + {C_2}{e^{{\lambda _2}t}}{\mathbf{V}_2},\] где \({\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T},\) \({\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T},\) − собственные векторы, соответствующие числам \({{\lambda _1},{\lambda _2}},\) а \({C_1},{C_2}\) − произвольные константы. Поскольку оба собственных значения отрицательны, то решение \(\mathbf{X} = \mathbf{0}\) является асимптотически устойчивым. Такое положение равновесия называется устойчивым узлом. При \(t \to \infty\) фазовые кривые стремятся к началу координат \(\mathbf{X} = \mathbf{0}.\) Уточним направление фазовых траекторий. Поскольку \[ {x\left( t \right) = {C_1}{V_{11}}{e^{{\lambda _1}t}} + {C_2}{V_{12}}{e^{{\lambda _2}t}},}\;\; {y\left( t \right) = {C_1}{V_{21}}{e^{{\lambda _1}t}} + {C_2}{V_{22}}{e^{{\lambda _2}t}},} \] то производная \(\large\frac{{dy}}{{dx}}\normalsize\) равна \[\frac{{dy}}{{dx}} = \frac{{{C_1}{V_{21}}{\lambda _1}{e^{{\lambda _1}t}} + {C_2}{V_{22}}{\lambda _2}{e^{{\lambda _2}t}}}}{{{C_1}{V_{11}}{\lambda _1}{e^{{\lambda _1}t}} + {C_2}{V_{12}}{\lambda _2}{e^{{\lambda _2}t}}}}.\] Разделим числитель и знаменатель на \({{e^{{\lambda _1}t}}}:\) \[\frac{{dy}}{{dx}} = \frac{{{C_1}{V_{21}}{\lambda _1} + {C_2}{V_{22}}{\lambda _2}{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}}}}{{{C_1}{V_{11}}{\lambda _1} + {C_2}{V_{12}}{\lambda _2}{e^{\left( {{\lambda _2} - {\lambda _1}} \right)t}}}}.\] В данном случае \({\lambda _2} - {\lambda _1} < 0.\) Поэтому члены с экспоненциальной функцией в пределе при \(t \to \infty\) стремятся к нулю. В результате при \({C_1} \ne 0\) получаем: \[\lim\limits_{t \to \infty } \frac{{dy}}{{dx}} = \frac{{{V_{21}}}}{{{V_{11}}}}.\] т.е. при \(t \to \infty\) фазовые траектории становятся параллельными собственному вектору \({\mathbf{V}_1}.\) В случае \({C_1} = 0\) производная при любом \(t\) равна \[\frac{{dy}}{{dx}} = \frac{{{V_{22}}}}{{{V_{12}}}},\] т.е. фазовая траектория лежит на прямой, направленной вдоль собственного вектора \({\mathbf{V}_2}.\) Теперь рассмотрим поведение фазовых траекторий при \(t \to -\infty.\) Очевидно, что координаты \(x\left( t \right),y\left( t \right)\) стремятся к бесконечности, а производная \(\large\frac{{dy}}{{dx}}\normalsize\) при \({C_2} \ne 0\) принимает следующий вид: \[\frac{{dy}}{{dx}} = \frac{{{C_1}{V_{21}}{\lambda _1}{e^{\left( {{\lambda _1} - {\lambda _2}} \right)t}} + {C_2}{V_{22}}{\lambda _2}}}{{{C_1}{V_{11}}{\lambda _1}{e^{\left( {{\lambda _1} - {\lambda _2}} \right)t}} + {C_2}{V_{12}}{\lambda _2}}} = \frac{{{V_{22}}}}{{{V_{12}}}},\] т.е. фазовые кривые в бесконечно удаленных точках становятся параллельными вектору \({\mathbf{V}_2}.\) Соответственно, при \({C_2} = 0\) производная равна \[\frac{{dy}}{{dx}} = \frac{{{V_{21}}}}{{{V_{11}}}}.\] В этом случае фазовая траектория определяется направлением собственного вектора \({\mathbf{V}_1}.\) С учетом рассмотренных свойств фазовых траекторий, фазовый портрет устойчивого узла имеет вид, показанный схематически на рисунке \(1.\)
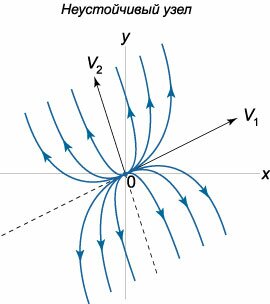
Корни \({{\lambda _1},{\lambda _2}}\) различны \(\left( {{\lambda _1} \ne {\lambda _2}} \right)\) и положительны \(\left( {{\lambda _1} > 0, {\lambda _2}} > 0\right).\) В этом случае точка \(\mathbf{X} = \mathbf{0}\) называется неустойчивым узлом. Ее фазовый портрет показан на рисунке \(2.\) Заметим, что в случае как устойчивого, так и неустойчивого узла фазовые траектории касаются прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине собственному значению \(\lambda.\)
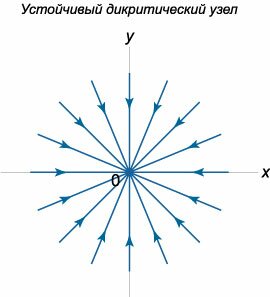
Дикритический узел
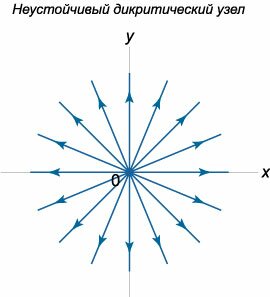
Пусть характеристическое уравнение имеет один нулевой корень кратности \(2,\) т.е. рассмотрим случай \({\lambda _1} = {\lambda _2} = {\lambda} \ne 0.\) При этом система имеет базис из двух собственных векторов, т.е. геометрическая кратность собственного значения \(\lambda\) равна \(2.\) В терминах линейной алгебры это означает, что размерность собственного подпространства матрицы \(A\) равна \(2:\) \(\dim \ker A = 2.\) Такая ситуация реализуется в системах вида \[ {\frac{{dx}}{{dt}} = \lambda x,}\;\; {\frac{{dy}}{{dt}} = \lambda y.} \] Направление фазовых траекторий зависит от знака \(\lambda.\) Здесь возможны следующие два случая:Случай \({\lambda _1} = {\lambda _2} = {\lambda} < 0.\) Такое положение равновесия называется устойчивым дикритическим узлом Случай \({\lambda _1} = {\lambda _2} = {\lambda} > 0.\) Данная комбинация собственных значений соответствует неустойчивому дикритическому узлу (рисунок \(4\)).
Вырожденный узел
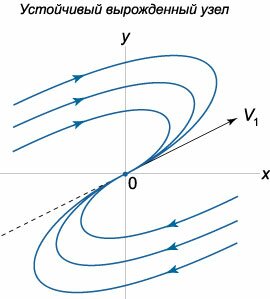
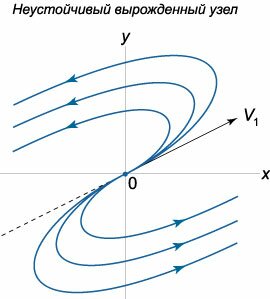
Пусть собственные значения матрицы \(A\) снова являются совпадающими: \({\lambda _1} = {\lambda _2} = {\lambda} \ne 0.\) В отличие от предыдущего случая дикритического узла предположим, что геометрическая кратность собственного значения (или другими словами размерность собственного подпространства) равна теперь \(1.\) Это означает, что матрица \(A\) имеет лишь один собственный вектор \({\mathbf{V}_1}.\) Второй линейно независимый вектор, необходимый для составления базиса, определяется как вектор \({\mathbf{W}_1},\) присоединенный к \({\mathbf{V}_1}.\)В случае \({\lambda _1} = {\lambda _2} = {\lambda} < 0\) точка равновесия называется устойчивым вырожденным узлом (рисунок \(5\)). При \({\lambda _1} = {\lambda _2} = {\lambda} > 0\) положение равновесия называется неустойчивым вырожденным узлом (рисунок \(6\)).
Седло
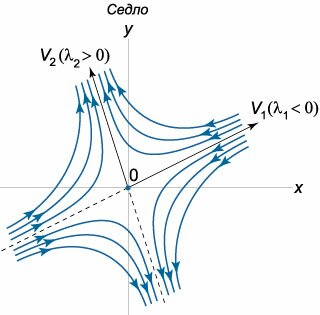
Положение равновесия является седлом при условиях \[{\lambda _1},{\lambda _2} \in \Re,\;\;{\lambda _1} \cdot {\lambda _2} < 0.\] Поскольку одно из собственных значений положительно, то седло является неустойчивой точкой равновесия. Пусть, например, \({\lambda _1} < 0,{\lambda _2} > 0.\) Собственные значения \({\lambda _1}\) и \({\lambda _2}\) ассоциируются с соответствующими собственными векторами \({\mathbf{V}_1}\) и \({\mathbf{V}_2}.\) Прямые, направленные вдоль собственных векторов \({\mathbf{V}_1},\) \({\mathbf{V}_2},\) называются сепаратрисами. Они являются асимптотами для остальных фазовых траекторий, имеющих форму гипербол. Каждой из сепаратрис можно сопоставить определенное направление движения. Если сепаратриса связана с отрицательным собственным значением \({\lambda _1} < 0,\) т.е. в данном случае направлена вдоль вектора \({\mathbf{V}_1},\) то движение вдоль нее происходит к точке равновесия \(\mathbf{X} = \mathbf{0}.\) И наоборот, при \({\lambda _2} > 0,\) т.е. для сепаратрисы, связанной с вектором \({\mathbf{V}_2},\) движение направлено от начала координат. Схематически фазовый портрет седла показан на рисунке \(7.\)
Устойчивый и неустойчивый фокус
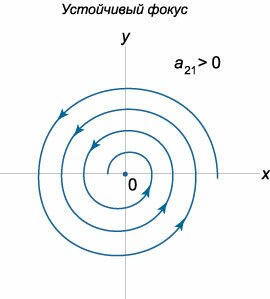
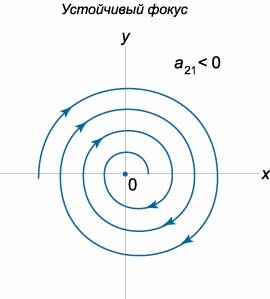
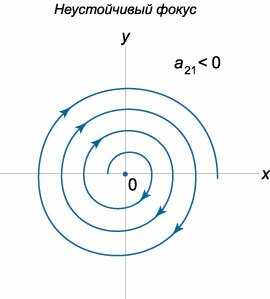
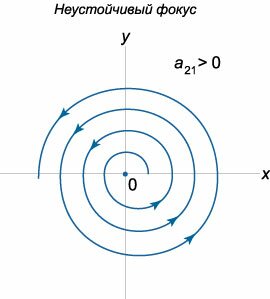
Пусть теперь собственные значения \({\lambda _1},{\lambda _2}\) являются комплексными числами, действительные части которых не равны нулю. Если матрица \(A\) состоит из действительных чисел, то комплексные корни будут представляться в виде комплексно-сопряженных чисел: \[{\lambda _{1,2}} = \alpha \pm i\beta .\] Выясним, какой вид имеют фазовые траектории в окрестности начала координат. Построим комплексное решение \({\mathbf{X}_1}\left( t \right)\) соответствующее собственному числу \({\lambda _1} = \alpha + i\beta :\) \[ {{\mathbf{X}_1}\left( t \right) = {e^{{\lambda _1}t}}{\mathbf{V}_1} } = {{e^{\left( {\alpha + i\beta } \right)t}}\left( {\mathbf{U} + i\mathbf{W}} \right),} \] где \({\mathbf{V}_1} = \mathbf{U} + i\mathbf{W}\) − комплекснозначный собственный вектор, ассоциированный с числом \({\lambda _1},\) \(\mathbf{U}\) и \(\mathbf{W}\) − действительные векторные функции. В результате преобразований получаем \[ {{\mathbf{X}_1}\left( t \right) = {e^{\alpha t}}{e^{i\beta t}}\left( {\mathbf{U} + i\mathbf{W}} \right) } = {{e^{\alpha t}}\left( {\cos \beta t + i\sin \beta t} \right)\left( {\mathbf{U} + i\mathbf{W}} \right) } = {{e^{\alpha t}}\left( {\mathbf{U}\cos \beta t + i\mathbf{U}\sin \beta t + i\mathbf{W}\cos \beta t - \mathbf{W}\sin \beta t} \right) } = {{e^{\alpha t}}\left( {\mathbf{U}\cos \beta t + - \mathbf{W}\sin \beta t} \right) } + {i{e^{\alpha t}}\left( {\mathbf{U}\sin \beta t + \mathbf{W}\cos \beta t} \right).} \] Действительная и мнимая части в последнем выражении образуют общее решение системы, которое имеет вид: \[ {\mathbf{X}\left( t \right) = {C_1}\text{Re}\left[ {{\mathbf{X}_1}\left( t \right)} \right] + {C_2}\text{Im}\left[ {{\mathbf{X}_1}\left( t \right)} \right] } = {{e^{\alpha t}}\left[ {{C_1}\left( {\mathbf{U}\cos \beta t - \mathbf{W}\sin \beta t} \right)} \right. } + {\left. {{C_2}\left( {\mathbf{U}\sin \beta t + \mathbf{W}\cos \beta t} \right)} \right] } = {{e^{\alpha t}}\left[ {\mathbf{U}\left( {{C_1}\cos \beta t + {C_2}\sin \beta t} \right)} \right. } + {\left. {\mathbf{W}\left( {{C_2}\cos \beta t - {C_1}\sin \beta t} \right)} \right].} \] Представим постоянные \({C_1},{C_2}\) в виде \[{C_1} = C\sin \delta ,\;\;{C_2} = C\cos \delta ,\] где \(\delta\) − некоторый вспомогательный угол. Тогда решение записывается как \[ {\mathbf{X}\left( t \right) = C{e^{\alpha t}}\left[ {\mathbf{U}\left( {\sin \delta \cos \beta t + \cos \delta \sin \beta t} \right)} \right. } + {\left. {\mathbf{W}\left( {\cos\delta \cos \beta t - \sin \delta \sin \beta t} \right)} \right] } = {C{e^{\alpha t}}\left[ {\mathbf{U}\sin \left( {\beta t + \delta } \right)} \right. + \left. {\mathbf{W}\cos \left( {\beta t + \delta } \right)} \right].} \] Таким образом, решение \(\mathbf{X}\left( t \right)\) раскладывается по базису, заданному векторами \(\mathbf{U}\) и \(\mathbf{W}:\) \[\mathbf{X}\left( t \right) = \mu \left( t \right)\mathbf{U} + \eta \left( t \right)\mathbf{W},\] где коэффициенты разложения \(\mu \left( t \right),\) \(\eta \left( t \right)\) определяются формулами: \[ {\mu \left( t \right) = C{e^{\alpha t}}\sin \left( {\beta t + \delta } \right),}\;\; {\eta \left( t \right) = C{e^{\alpha t}}\cos\left( {\beta t + \delta } \right).} \] Отсюда видно, что фазовые траектории представляют собой спирали. При \(\alpha < 0\) спирали будут закручиваться, приближаясь к началу координат. Такое положение равновесия называется устойчивым фокусом. Соответственно, при \(\alpha > 0\) мы имеем неустойчивый фокус.Направление закручивания спиралей можно определить по знаку коэффициента \({a_{21}}\) в исходной матрице \(A.\) Действительно, рассмотрим производную \(\large\frac{{dy}}{{dt}}\normalsize,\) например, в точке \(\left( {1,0} \right):\) \[\frac{{dy}}{{dt}}\left( {1,0} \right) = {a_{21}} \cdot 1 + {a_{22}} \cdot 0 = {a_{21}}.\] Положительный коэффициент \({a_{21}} > 0\) соответствует закручиванию спиралей против часовой стрелки, как показано на рисунке \(8.\) При \({a_{21}} < 0\) спирали будут закручиваться по часовой стрелке (рисунок \(9\)). Таким образом, с учетом направления закручивания спиралей, всего существует \(4\) различных вида фокуса. Схематически они показаны на рисунках \(8-11.\)
Центр
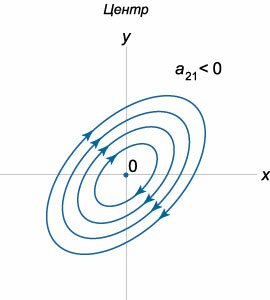
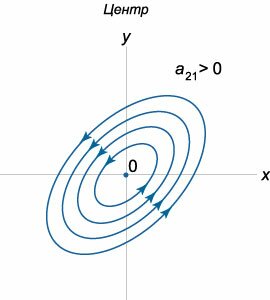
Если собственные значения матрицы \(A\) являются число мнимыми числами, то такое положение равновесия называется центром. Для матрицы с действительными элементами мнимые собственные значения будут комплексно-сопряженными. В случае центра фазовые траектории формально получаются из уравнения спиралей при \(\alpha = 0\) и представляют собой эллипсы, т.е. описывают периодическое движение точки на фазовой плоскости. Положения равновесия типа "центр" являются устойчивыми по Ляпунову.Возможны два вида центра, различающиеся направлением движения точек (рисунки \(12, 13\)). Как и в случае спиралей, направление движения можно определить, например, по знаку производной \(\large\frac{{dy}}{{dt}}\normalsize\) в какой-либо точке. Если взять точку \(\left( {1,0} \right),\) то \[\frac{{dy}}{{dt}}\left( {1,0} \right) = {a_{21}}.\] т.е. направление вращения определяется знаком коэффициента \({a_{21}}.\)
Теперь обратимся к случаю вырожденной матрицы \(A.\)
Вырожденная матрица
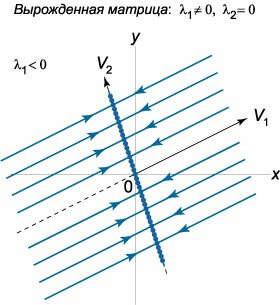
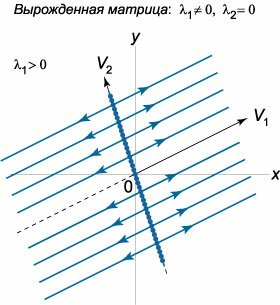
Если матрица является вырожденной, то у нее одно или оба собственных значения равны нулю. При этом возможны следующие частные случаи:Случай \({\lambda _1} \ne 0, {\lambda _2} = 0\). Здесь общее решение записывается в виде \[\mathbf{X}\left( t \right) = {C_1}{e^{{\lambda _1}t}}{\mathbf{V}_1} + {C_2}{\mathbf{V}_2},\] где \({\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T},\) \({\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T},\) − собственные векторы, соответствующие числам \({\lambda _1}\) и \({\lambda _2}.\) Оказывается, что в данном случае вся прямая, проходящая через начало координат и направленная вдоль вектора \({\mathbf{V}_2},\) состоит из точек равновесия (эти точки не имеют специального названия). Фазовые траектории представляют собой лучи, параллельные другому собственному вектору \({\mathbf{V}_1}.\) В зависимости от знака \({\lambda _1}\) движение при \(t \to \infty\) происходит либо в направлении прямой \({\mathbf{V}_2}\) (рис.\(14\)), либо от нее (рис.\(15\)).
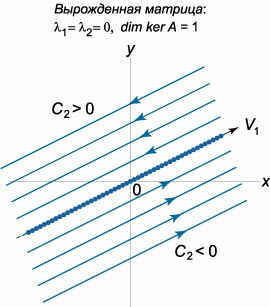
В этом случае размерность собственного подпространства матрицы равна \(2\) и, следовательно, существуют два собственных вектора \({\mathbf{V}_1}\) и \({\mathbf{V}_2}.\) Такая ситуация возможна при нулевой матрице \(A.\) Общее решение выражается формулой \[\mathbf{X}\left( t \right) = {C_1}{\mathbf{V}_1} + {C_2}{\mathbf{V}_2}.\] Отсюда следует, что любая точка плоскости является положением равновесия системы. Случай \({\lambda _1} = {\lambda _2} = 0, \dim \ker A = 1.\) Данный случай вырожденной матрицы отличается от предыдущего тем, что существует лишь \(1\) собственный вектор (Матрица \(A\) при этом будет ненулевой). Для построения базиса в качестве второго линейно независимого вектора можно взять вектор \({\mathbf{W}_1},\) присоединенный к \({\mathbf{V}_1}.\) Общее решение системы записывается в виде \[\mathbf{X}\left( t \right) = \left( {{C_1} + {C_2}t} \right){\mathbf{V}_1} + {C_2}{\mathbf{W}_1}.\] Здесь все точки прямой, проходящей через начало координат и направленной вдоль собственного вектора \({\mathbf{V}_1},\) являются неустойчивыми положениями равновесия. Фазовые траектории представляют собой прямые, параллельные \({\mathbf{V}_1}.\) Направление движения вдоль этих прямых при \(t \to \infty\) зависит от постоянной \({C_2}:\) при \({C_2} < 0\) движение происходит слева направо, а при \({C_2} > 0\) − в противоположную сторону (рис.\(16\)). Как видно, в случае вырожденной матрицы существует \(4\) различных фазовых портрета, Таким образом, линейная автономная система второго порядка допускает всего \(17\) различных фазовых портретов.
Бифуркационная диаграмма
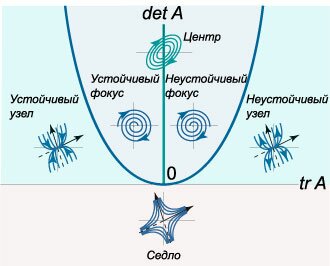
Выше мы рассмотрели классификацию положений равновесия линейной системы, основанную на собственных значениях. Однако тип точки равновесия можно определить и без вычисления собственных значений \({\lambda _1},{\lambda _2},\) а зная лишь только определитель матрицы \(\det A\) и ее след \(\text{tr}\,A.\)Напомним, что следом матрицы называется число, равное сумме диагональных элементов: \[ {A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right),}\;\; {\text{tr}\,A = {a_{11}} + {a_{22}},}\;\; {\det A = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}.} \] Действительно, характеристическое уравнение матрицы имеет следующий вид: \[{\lambda ^2} - \left( {{a_{11}} + {a_{22}}} \right)\lambda + {a_{11}}{a_{22}} - {a_{12}}{a_{21}} = 0.\] Его можно записать через определитель и след матрицы: \[{\lambda ^2} - \text{tr}\,A \cdot \lambda + \det A = 0.\] Дискриминант этого квадратного уравнения определяется соотношением \[D = {\left( {\text{tr}\,A} \right)^2} - 4\det A.\] Таким образом, бифуркационная кривая, разграничивающая различные режимы устойчивости, представляет собой параболу на плоскости \(\left( {\text{tr}\,A,\det A} \right)\) (рис.\(17\)): \[\det A = {\left( {\frac{\text{tr}\,A}{2}} \right)^2}.\] Выше параболы находятся точки равновесия типа фокус и центр. Точки типа "центр" расположены на положительной полуоси \(Oy,\) т.е. при условии \(\text{tr}\,A = 0.\) Ниже параболы находятся точки типа "узел" или "седло". Сама парабола содержит дикритические или вырожденные узлы. Устойчивые режимы движения существуют в левом верхнем квадранте бифуркационной диаграммы. Остальные три квадранта соответствуют неустойчивым положениям равновесия.
Алгоритм построения фазового портрета
Для схематического построения фазового портрета линейной автономной системы \(2\)-го порядка с постоянными коэффициентами \[ {\mathbf{X'} = A\mathbf{X},}\;\; {A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right),}\;\; {\mathbf{X} = \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right)} \] необходимо выполнить следующие действия:
Описанный алгоритм не является жесткой схемой. При исследовании конкретной системы вполне допустимы различные вариации и другие приемы, позволяющие в итоге изобразить фазовый портрет. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
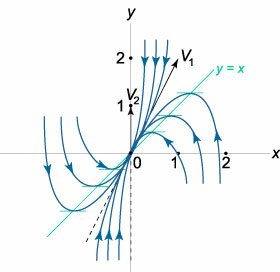
Исследовать положения равновесия линейной автономной системы и начертить ее фазовый портрет. \[\frac{{dx}}{{dt}} = - x,\;\;\frac{{dy}}{{dt}} = 2x - 2y.\]
Решение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
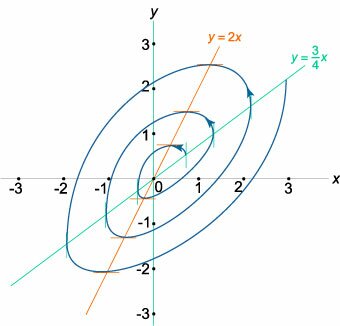
Исследовать положения равновесия динамической системы и схематически изобразить ее фазовый портрет. \[\frac{{dx}}{{dt}} = x + 3y,\;\;\frac{{dy}}{{dt}} = 2x.\]
Решение.
Убедимся сначала, что определитель матрицы не равен нулю: \[ {A = \left( {\begin{array}{*{20}{c}} 1&3\\ 2&0 \end{array}} \right),}\;\; {\det A = \left| {\begin{array}{*{20}{c}} 1&3\\ 2&0 \end{array}} \right| = - 6 \ne 0.} \] Следовательно, система имеет единственную точку равновесия в начале координат.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
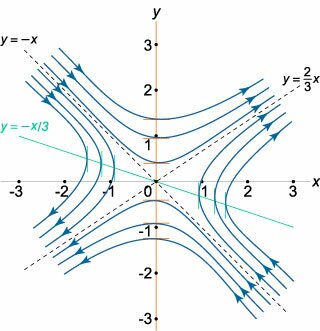
Исследовать точки равновесия и начертить фазовый портрет следующей системы: \[\frac{{dx}}{{dt}} = 3x - 4y,\;\;\frac{{dy}}{{dt}} = 2x - y.\]
Решение.
Определитель матрицы данной системы равен \[ {A = \left( {\begin{array}{*{20}{c}} 3&{ - 4}\\ 2&{ - 1} \end{array}} \right),}\;\; {\det A = \left| {\begin{array}{*{20}{c}} 3&{ - 4}\\ 2&{ - 1} \end{array}} \right| = 5 \ne 0.} \] Следовательно, система имеет единственное положение равновесия в точке \(\left( {0,0} \right).\)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Исследовать устойчивость системы в зависимости от параметра \(a:\) \[\frac{{dx}}{{dt}} = ax + y,\;\;\frac{{dy}}{{dt}} = x + ay.\]
Решение.
Вычислим след и определитель матрицы \(A:\) \[ {A = \left( {\begin{array}{*{20}{c}} a&1\\ 1&a \end{array}} \right),}\;\; {\text{tr}\,A = 2a,}\;\; {\det A = {a^2} - 1.} \] Характеристическое уравнение данной системы записывается в виде \[ {{\lambda ^2} - \text{tr}\,A \cdot \lambda + \det A = 0,}\;\; {\Rightarrow {\lambda ^2} - 2a\lambda + {a^2} - 1 = 0.} \] Дискриминант этого уравнения равен \[\require{cancel} {D = {\left( { - 2a} \right)^2} - 4\left( {{a^2} - 1} \right) } = {\cancel{4{a^2}} - \cancel{4{a^2}} + 4 = 4 > 0.} \] Поскольку дискриминант всегда положителен, то при любом \(a\) собственные значения будут действительными. Это значит, что при \(\det A \ne 0\) система имеет единственное положение равновесия в начале координат, которое будет являться либо седлом, либо узлом.Выясним, при каких значениях \(a\) нулевая точка будет седлом. Согласно бифуркационной диаграмме седло существует при условии \(\det A < 0.\) Получаем неравенство: \[\det A = {a^2} - 1 < 0,\;\; \Rightarrow a \in \left( { - 1,1} \right).\] Таким образом, при \(a \in \left( { - 1,1} \right)\) в начале координат будет существовать седло. Ясно, что положение равновесия типа "узел" существует при следующих значениях параметра \(a:\) \[a \in \left( { - \infty , - 1} \right) \cup \left( {1,\infty } \right).\] Причем, если \(\text{tr}\,A = 2a > 0\) или \(a > 0,\) то узел будет неустойчивым, а при \(\text{tr}\,A = 2a < 0\) или при \(a < 0\) − получаем устойчивый узел. В результате имеем: \[a \in \left( {1,\infty } \right) - \text{неустойчивый узел},\] \[a \in \left( {-\infty,-1 } \right) - \text{устойчивый узел}.\] Заметим, что ни при каких \(a\) мы не попадаем на саму параболу на бифуркационной диаграмме. Действительно, уравнение указанной параболы имеет вид \[\det A = {\left( {\frac{\text{tr}\,A}{2}} \right)^2}.\] При подстановке наших значений, получаем \[ {{a^2} - 1 = {\left( {\frac{{2a}}{2}} \right)^2},}\;\; {\Rightarrow {a^2} - 1 = {a^2},}\;\; {\Rightarrow - 1 = 0,} \] что неверно. Рассмотрим отдельно случаи в граничных точках \(a = \pm 1.\) При таких значениях \(a\) система становится вырожденной: \[\det A = {a^2} - 1 = 0.\] Пусть \(a = 1.\) Вычислим собственные значения матрицы: \[ {A = \left( {\begin{array}{*{20}{c}} 1&1\\ 1&1 \end{array}} \right),}\;\; {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} {1 - \lambda }&1\\ 1&{1 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\left( {\lambda - 1} \right)^2} - 1 = 0,}\;\; {\Rightarrow \left| {\lambda - 1} \right| = 1,}\;\; {\Rightarrow {\lambda _{1,2}} = 1 \pm 1 = 0,\;2.} \] Определим собственный вектор \({\mathbf{V}_1},\) соответствующий значению \({\lambda_1} = 0:\) \[ {\left( {\begin{array}{*{20}{c}} {1 - 0}&1\\ 1&{1 - 0} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{c}} 1&1\\ 1&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{V_{11}}}\\ {{V_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow {V_{11}} + {V_{21}} = 0,}\;\; {\Rightarrow {V_{21}} = 1,\;{V_{11}} = - 1,}\;\; {\Rightarrow {\mathbf{V}_1} = \left( {\begin{array}{*{20}{c}} { - 1}\\ 1 \end{array}} \right).} \] Следовательно, прямая, параллельная вектору \({\mathbf{V}_1},\) и проходящая через начало координат, имеет уравнение \(y = -x.\) Любая точка этой прямой является точкой равновесия, причем эти положения равновесия являются неустойчивыми, поскольку второе собственное значение положительное: \({\lambda_2} = 2 > 0.\) Пусть теперь \(a = -1.\) Аналогично найдем собственные значения матрицы при этом \(a:\) \[ {A = \left( {\begin{array}{*{20}{r}} { - 1}&1\\ 1&{ - 1} \end{array}} \right),}\;\; {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - 1 - \lambda }&1\\ 1&{ - 1 - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow {\left( {\lambda + 1} \right)^2} - 1 = 0,}\;\; {\Rightarrow \left| {\lambda + 1} \right| = 1,}\;\; {\Rightarrow {\lambda _{1,2}} = - 1 \pm 1 = 0,\; - 2.} \] Вычислим собственный вектор \({\mathbf{U}_1} = {\left( {{U_{11}},{U_{21}}} \right)^T},\) соответствующий числу \({\lambda_1} = 0:\) \[ {\left( {\begin{array}{*{20}{c}} { - 1 - 0}&1\\ 1&{ - 1 - 0} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{U_{11}}}\\ {{U_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left( {\begin{array}{*{20}{r}} { - 1}&1\\ 1&{ - 1} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{U_{11}}}\\ {{U_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow - {U_{11}} + {U_{21}} = 0,}\;\; {\Rightarrow {U_{21}} = 1,\;{U_{11}} = 1,}\;\; {\Rightarrow {\mathbf{U}_1} = \left( {\begin{array}{*{20}{c}} {{U_{11}}}\\ {{U_{21}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right).} \] Этому вектору соответствует прямая \(y = x,\) проходящая через начало координат. Все точки этой прямой являются положениями равновесия. Данное равновесие будет устойчивым, поскольку \({\lambda_2} = -2 < 0.\) Собирая вместе полученные результаты, запишем окончательный ответ. Система имеет следующие положения равновесия в зависимости от параметра \(a:\)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||