|
Повторные интегралы
|
||||||
|
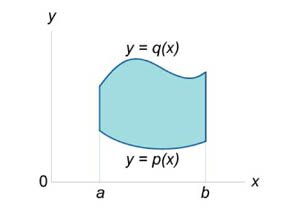
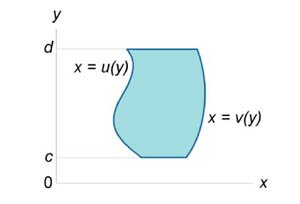
Области интегрирования \(I\) и \(II\) типа
Двойные интегралы вычисляются, как правило, с помощью повторных интегралов. Однако переход от двойных к повторным интегралам возможен не для произвольной области интегрирования \(R,\) а для областей определенного типа. Введем понятия областей интегрирования типа \(I\) и \(II.\)Определение \(1\). Говорят, что область \(R\) на плоскости относится к типу \(I\) или является элементарной относительно оси \(Oy\), если она лежит между графиками двух непрерывных функций, зависящих от \(x\) (рисунок \(1\)), и описывается множеством: \[R = \left\{ {\left( {x,y} \right)|\;a \le x \le b,\;p\left( x \right) \le y \le q\left( x \right)} \right\}.\] Определение \(2\). Говорят, что область \(R\) на плоскости относится к типу \(II\) или является элементарной относительно оси \(Ox\), если она лежит между графиками двух непрерывных функций, зависящих от \(y\) (рисунок \(2\)), и описывается множеством: \[R = \left\{ {\left( {x,y} \right)|\;u\left( y \right) \le x \le v\left( y \right),\;c \le y \le d} \right\}.\]
Связь между двойными и повторными интегралами
Пусть \(f\left( {x,y} \right)\) является непрерывной функцией в области \(R\) типа \(I:\) \[R = \left\{ {\left( {x,y} \right)|\;a \le x \le b,\;p\left( x \right) \le y \le q\left( x \right)} \right\}.\] Тогда двойной интеграл от функции \(f\left( {x,y} \right)\) в данной области выражается через повторный интеграл в виде \[ {\iint\limits_R {f\left( {x,y} \right)dA} } = {\int\limits_a^b {\int\limits_{p\left( x \right)}^{q\left( x \right)} {f\left( {x,y} \right)dydx} } .} \] Для области интегрирования типа \(II\) существует аналогичная формула. Если \(f\left( {x,y} \right)\) является непрерывной функцией в области \(R\) типа \(II:\) \[R = \left\{ {\left( {x,y} \right)|\;u\left( y \right) \le x \le v\left( y \right),\;c \le y \le d} \right\},\] то справедливо соотношение \[ {\iint\limits_R {f\left( {x,y} \right)dA} } = {\int\limits_c^d {\int\limits_{u\left( y \right)}^{v\left( y \right)} {f\left( {x,y} \right)dxdy} } .} \] Приведенные формулы (в англоязычной литературе они известны как теорема Фубини) позволяют вычислять двойные интегралы через повторные. В повторных интегралах сначала находится внутренний интеграл, а затем - внешний. |
||||||
|
Пример 1
|
||||||
|
Найти повторный интеграл \(\int\limits_0^1 {\int\limits_1^2 {xydydx} } .\)
Решение. |
||||||
|
Пример 2
|
||||||
|
Найти повторный интеграл \(\int\limits_0^1 {\int\limits_y^{{y^2}} {\left( {x + 2y} \right)dxdy} }.\)
Решение. |
||||||
|
Пример 3
|
||||||
|
Вычислить \(\int\limits_1^2 {\int\limits_0^y {x\sqrt {{y^2} + {x^2}} dxdy} }.\)
Решение. |
||||||
|
Пример 4
|
||||||
|
Вычислить \(\int\limits_0^1 {\int\limits_0^y {\ln \left( {{y^2} + 1} \right)dxdy} } .\)
Решение. |
||||||
|
Пример 5
|
||||||
|
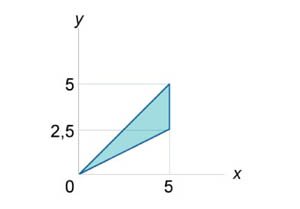
Изменить порядок интегрирования в повторном интеграле \(I = \int\limits_0^5 {\int\limits_{\frac{x}{2}}^x {f\left( {x,y} \right)dydx} } .\)
Решение.
|
||||||