Поверхностные интегралы второго рода

Рассмотрим векторное поле \(\mathbf{F}\left( {x,y,z} \right)\) и поверхность \(S,\) которая описывается вектором \[ {\mathbf{r}\left( {u,v} \right) } = {x\left( {u,v} \right) \cdot \mathbf{i} + y\left( {u,v} \right) \cdot \mathbf{j} + z\left( {u,v} \right) \cdot \mathbf{k}.} \] Предполагается, что функции \(x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)\) являются непрерывно дифференцируемыми в некоторой области \(D\left( {u,v} \right),\) и что ранг матрицы \[\left( {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial z}}{{\partial u}}}\\ {\frac{{\partial x}}{{\partial v}}}&{\frac{{\partial y}}{{\partial v}}}&{\frac{{\partial z}}{{\partial v}}} \end{array}} \right)\] равен \(2.\)

Обозначим через \(\mathbf{n}\left( {x,y,z} \right)\) единичный нормальный вектор к поверхности \(S\) в точке \(\left( {x,y,z} \right).\) Если поверхность \(S\) гладкая и векторная функция \(\mathbf{n}\left( {x,y,z} \right)\) непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора: \[\mathbf{n}\left( {x,y,z} \right)\;\;\text{или}\;\; - \mathbf{n}\left( {x,y,z} \right).\] Выбор одного из них называется ориентацией поверхности.

Если \(S\) является границей ограниченной области, то ее можно ориентировать внешней или внутренней нормалями. Поверхность \(S,\) ориентированную внешней нормалью, называют ее внешней стороной, а ориентированную внутренней нормалью, − ее внутренней стороной.

Поверхностный интеграл второго рода от векторного поля \(\mathbf{F}\) по ориентированной поверхности \(S\) (или поток векторного поля \(\mathbf{F}\) через поверхность \(S\)) может быть записан в одной из следующих форм:

• Если поверхность \(S\) ориентирована внешней нормалью, то \[ {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot \mathbf{n}dS} } = {\iint\limits_{D\left( {u,v} \right)} {\mathbf{F}\left( {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right) \cdot \left[ {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right]dudv} ;} \]

• Если поверхность \(S\) ориентирована внутренней нормалью, то \[ {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot \mathbf{n}dS} } = {\iint\limits_{D\left( {u,v} \right)} {\mathbf{F}\left( {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right) \cdot \left[ {\frac{{\partial \mathbf{r}}}{{\partial v}} \times \frac{{\partial \mathbf{r}}}{{\partial u}}} \right]dudv}.} \]

Величина \(d\mathbf{S} = \mathbf{n}dS\) называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом: \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} } = {\frac{{\partial x}}{{\partial u}}\left( {u,v} \right) \cdot \mathbf{i} + \frac{{\partial y}}{{\partial u}}\left( {u,v} \right) \cdot \mathbf{j} + \frac{{\partial z}}{{\partial u}}\left( {u,v} \right) \cdot \mathbf{k},} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial v}} } = {\frac{{\partial x}}{{\partial v}}\left( {u,v} \right) \cdot \mathbf{i} + \frac{{\partial y}}{{\partial v}}\left( {u,v} \right) \cdot \mathbf{j} + \frac{{\partial z}}{{\partial v}}\left( {u,v} \right) \cdot \mathbf{k}.} \] Если поверхность \(S\) задана явно в виде уравнения \(z = z\left( {x,y} \right),\) где \(z\left( {x,y} \right)\) − дифференцируемая функция в области \(D\left( {x,y} \right),\) то поверхностный интеграл второго рода от векторного поля \(\mathbf{F}\) по поверхности \(S\) записывается в одной из следующих форм:

• Если поверхность \(S\) ориентирована внешней нормалью (\(k\)-компонент вектора нормали является положительным), то \[ {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot \mathbf{n}dS} } = {\iint\limits_{D\left( {x,y} \right)} {\mathbf{F}\left( {x,y,z} \right) \cdot \left( { - \frac{{\partial z}}{{\partial x}}\mathbf{i} - \frac{{\partial z}}{{\partial y}}\mathbf{j} + \mathbf{k}} \right)dxdy} ;} \]

• Если поверхность \(S\) ориентирована внутренней нормалью (\(k\)-компонент вектора нормали является отрицательным), то \[ {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot d\mathbf{S}} } = {\iint\limits_S {\mathbf{F}\left( {x,y,z} \right) \cdot \mathbf{n}dS} } = {\iint\limits_{D\left( {x,y} \right)} {\mathbf{F}\left( {x,y,z} \right) \cdot \left( { \frac{{\partial z}}{{\partial x}}\mathbf{i} + \frac{{\partial z}}{{\partial y}}\mathbf{j} - \mathbf{k}} \right)dxdy}.} \]

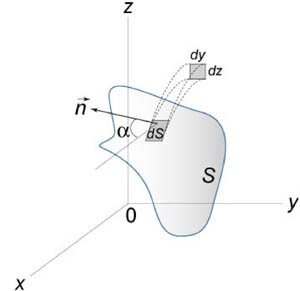
Поверхностный интеграл второго рода можно записать также в координатной форме. Пусть \(P\left( {x,y,z} \right),\) \(Q\left( {x,y,z} \right),\) \(R\left( {x,y,z} \right)\) являются компонентами векторного поля \(\mathbf{F}.\) Введем \(\cos \alpha,\) \(\cos \beta,\) \(\cos \gamma\) − направляющие косинусы внешней нормали \(\mathbf{n}\) к поверхности \(S.\) Тогда скалярное произведение \(\mathbf{F} \cdot \mathbf{n}\) равно \[ {\mathbf{F} \cdot \mathbf{n} } = {\mathbf{F}\left( {P\left( {x,y,z} \right),Q\left( {x,y,z} \right),R\left( {x,y,z} \right)} \right) \cdot \mathbf{n}\left( {\cos \alpha ,\cos \beta ,\cos \gamma } \right) } = {P\cos \alpha + Q\cos \beta + R\cos \gamma .} \] Следовательно, поверхностный интеграл можно записать в виде \[ {\iint\limits_S {\left( {\mathbf{F} \cdot \mathbf{n}} \right)dS} } = {\iint\limits_S {\left( {P\cos \alpha + Q\cos \beta + R\cos \gamma } \right)dS} .} \] Поскольку \(\cos \alpha \cdot dS = dydz\) (рисунок \(1\)), и, аналогично, \(\cos \beta \cdot dS = dzdx,\) \(\cos \gamma \cdot dS = dxdy,\) получаем следующую формулу для вычисления поверхностного интеграла \(II\) рода: \[ {\iint\limits_S {\left( {\mathbf{F} \cdot \mathbf{n}} \right)dS} } = {\iint\limits_S {\left( {P\cos \alpha + Q\cos \beta + R\cos \gamma } \right)dS} } = {\iint\limits_S {Pdydz + Qdzdx + Rdxdy} .} \] Если поверхность \(S\) задана в параметрической форме с помощью вектора \(\mathbf{r}\left( {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right),\) то последняя формула принимает вид \[ {\iint\limits_S {\left( {\mathbf{F} \cdot \mathbf{n}} \right)dS} } = {\iint\limits_S {Pdydz + Qdzdx + Rdxdy} } = {\iint\limits_{D\left( {u,v} \right)} {\left| {\begin{array}{*{20}{c}} P&Q&R\\ {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial z}}{{\partial u}}}\\ {\frac{{\partial x}}{{\partial v}}}&{\frac{{\partial y}}{{\partial v}}}&{\frac{{\partial z}}{{\partial v}}} \end{array}} \right|dudv} ,} \] где \(\left( {u,v} \right)\) изменяются в пределах области интегрирования \(D\left( {u,v} \right).\) Если поверхность \(S\) не представима в явном или параметрическом виде, то ее можно попробовать разбить на конечное число частей, каждая из которых представима в таком виде. В этом случае справедливо свойство аддитивности: поверхностный интеграл второго рода по поверхности \(S\) будет равен сумме интегралов по ее частям.

   Пример 1

Вычислить поверхностный интеграл от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {x, - 1,z} \right)\) по внутренне ориентированной поверхности \(S,\) заданной уравнением \(z = x\cos y,\) где \(0 \le x \le 1,\) \(\large\frac{\pi }{4}\normalsize \le y \le \large\frac{\pi }{3}\normalsize.\) Применим формулу \[ {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iint\limits_{D\left( {x,y} \right)} {\mathbf{F} \cdot \left( {\frac{{\partial z}}{{\partial x}}\mathbf{i} + \frac{{\partial z}}{{\partial y}}\mathbf{j} - \mathbf{k}} \right)dxdy} .} \] Поскольку \[ {\frac{{\partial z}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {x\cos y} \right) = \cos y,}\;\; {\frac{{\partial z}}{{\partial y}} = \frac{\partial }{{\partial y}}\left( {x\cos y} \right) = - x\sin y,} \] то поверхностный интеграл можно записать в виде \[\require{cancel} {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iint\limits_{D\left( {x,y} \right)} {\left[ {x \cdot \cos y + \left( { - 1} \right) \cdot \left( { - x\sin y} \right) + z \cdot \left( { - 1} \right)} \right]dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {\left( {\cancel{x\cos y} + x\sin y - \cancel{x\cos y}} \right)dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {x\sin ydxdy} .} \] В результате простых вычислений находим ответ: \[ {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\int\limits_0^1 {xdx} \int\limits_{\large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{3}\normalsize} {\sin ydy} } = {\left[ {\left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^1} \right] \cdot \left[ {\left. {\left( { - \cos y} \right)} \right|_{\large\frac{\pi }{4}\normalsize}^{\large\frac{\pi }{3}\normalsize}} \right] } = {\frac{1}{2}\left( { - \cos \frac{\pi }{3} + \cos \frac{\pi }{4}} \right) } = {\frac{1}{2}\left( { - \frac{1}{2} + \frac{{\sqrt 2 }}{2}} \right) } = {\frac{{\sqrt 2 - 1}}{4}.} \]

   Пример 2

Найти интеграл от векторного поля \(\mathbf{F}\left( {x,y,z} \right) = \left( {y,x,z} \right)\) по поверхности \(S,\) заданной в параметрической форме вектором \(\mathbf{r}\left( {u,v} \right) = \left( {\cos v,\sin v,u} \right),\) \(0 \le u \le 2,\) \(\large\frac{\pi }{2}\normalsize \le v \le \pi .\) Сначала найдем частные производные. \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} = \left( {0,0,1} \right),}\;\; {\frac{{\partial \mathbf{r}}}{{\partial v}} = \left( { - \sin v,\cos v,0} \right).} \] Отсюда следует, что \[ {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ 0&0&1\\ { - \sin v}&{\cos v}&0 \end{array}} \right| } = { - \cos v \cdot \mathbf{i} - \sin v \cdot \mathbf{j}.} \] Следовательно, векторный элемент площади равен \[ {d\mathbf{S} = \left[ {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right]dudv } = {\left( { - \cos v, - \sin v,0} \right)dudv.} \] Так как \(x = \cos v, y = \sin v\) и \(z = v,\) то векторное поле \(\mathbf{F}\) можно представить в виде: \[\mathbf{F}\left( {r,u,v} \right) = \left( {\sin v,\cos v,u} \right).\] Тогда исходный поверхностный интеграл равен \[ {\iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iint\limits_{D\left( {u,v} \right)} {\left[ {\sin v \cdot \left( { - \cos v} \right) + \cos v \cdot \left( { - \sin v} \right) + 0} \right]dudv} } = {\iint\limits_{D\left( {u,v} \right)} {\left( { - 2\sin v\cos v} \right)dudv} } = { - \int\limits_0^2 {du} \int\limits_{\large\frac{\pi }{2}\normalsize}^\pi {\sin 2vdv} } = { - 2 \cdot \left[ {\left. {\left( { - \frac{{\cos 2v}}{2}} \right)} \right|_{\large\frac{\pi }{2}\normalsize}^\pi } \right] } = {\cos 2\pi - \cos \pi = 2.} \]

   Пример 3

Оценить поток векторного поля \(\mathbf{F} = y \cdot \mathbf{i} - x \cdot \mathbf{j} + z \cdot \mathbf{k}\) через коническую поверхность \(z = \sqrt {{x^2} + {y^2}} ,\) \(0 \le z \le 2,\) ориентированную внешней стороной. Поверхность конуса можно описать вектором \(\mathbf{r}:\) \[\mathbf{r}\left( {x,y} \right) = x \cdot \mathbf{i} + y \cdot \mathbf{j} + \sqrt {{x^2} + {y^2}} \cdot \mathbf{k}.\] Область интегрирования \(D\left( {x,y} \right)\) представляет собой круг \({{x^2} + {y^2}} \le 4.\)
Найдем векторный элемент площади \(d\mathbf{S},\) перпендикулярный поверхности и направленный во внешнюю сторону. Определим частные производные: \[ {\frac{{\partial \mathbf{r}}}{{\partial x}} = 1 \cdot \mathbf{i} + \frac{x}{{\sqrt {{x^2} + {y^2}} }} \cdot \mathbf{k},}\;\; {\frac{{\partial \mathbf{r}}}{{\partial y}} = 1 \cdot \mathbf{j} + \frac{y}{{\sqrt {{x^2} + {y^2}} }} \cdot \mathbf{k}.} \] Тогда \[ {\frac{{\partial \mathbf{r}}}{{\partial x}} \times \frac{{\partial \mathbf{r}}}{{\partial y}} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ 1 & 0 & {\frac{x}{{\sqrt {{x^2} + {y^2}} }}}\\ 0 & 1 & {\frac{y}{{\sqrt {{x^2} + {y^2}} }}} \end{array}} \right| } = { - \frac{x}{{\sqrt {{x^2} + {y^2}} }} \cdot \mathbf{i} - \frac{y}{{\sqrt {{x^2} + {y^2}} }} \cdot \mathbf{j} + \mathbf{k},} \] и векторный элемент равен \[d\mathbf{S} = \left( { - \frac{x}{{\sqrt {{x^2} + {y^2}} }}, - \frac{y}{{\sqrt {{x^2} + {y^2}} }},1} \right)dxdy.\] Векторное поле \(\mathbf{F}\) на поверхности конуса можно записать в виде \[ {\mathbf{F}\left( {x,y,z} \right) } = {y \cdot \mathbf{i} - x \cdot \mathbf{j} + \sqrt {{x^2} + {y^2}} \cdot \mathbf{k}.} \] Отсюда следует, что поток векторного поля через поверхность \(S\) (или, другими словами, поверхностный интеграл \(II\) рода) равен \[ {I = \iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} } = {\iint\limits_{D\left( {x,y} \right)} {\left[ {y \cdot \left( { - \frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right) + \left( { - x} \right) \cdot \left( { - \frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right) + \sqrt {{x^2} + {y^2}} \cdot 1} \right]dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {{x^2} + {y^2}} dxdy} .} \] Значение последнего интеграла легко вычисляется в полярных координатах. \[ {I = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^1 {{r^2}dr} } = {2\pi \cdot \left[ {\left. {\left( {\frac{{{r^3}}}{3}} \right)} \right|_0^1} \right] } = {\frac{{2\pi }}{3}.} \]

   Пример 4

Оценить поток векторного поля \(\mathbf{F}\left( {x,y,z} \right) = - y \cdot \mathbf{i} + x \cdot \mathbf{j} - z \cdot \mathbf{k}\) через внутреннюю сторону единичной сферы \({x^2} + {y^2} + {z^2} = 1.\) Запишем уравнение единичной сферы в сферических координатах: \[\mathbf{r}\left( {\psi ,\theta } \right) = \cos \psi \sin \theta \cdot \mathbf{i} + \sin \psi \sin \theta \cdot \mathbf{j} + \cos \theta \cdot \mathbf{k},\] где \(0 \le \psi \le 2\pi ,\) \(0 \le \theta \le \pi.\) В результате вектор \(\mathbf{F}\) на заданной поверхности можно записать в виде \[ {\mathbf{F}\left( {r,\psi ,\theta } \right) } = { - \sin \psi \sin \theta \cdot \mathbf{i} + \cos \psi \sin \theta \cdot \mathbf{j} - \cos \theta \cdot \mathbf{k},} \] Вычислим векторный элемент площади \(d\mathbf{S}.\) Частные производные равны \[ {\frac{{\partial \mathbf{r}}}{{\partial \psi }} } = { - \sin \psi \sin \theta \cdot \mathbf{i} + \cos \psi \sin \theta \cdot \mathbf{j} + 0 \cdot \mathbf{k},} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial \theta }} } = {\cos \psi \sin \theta \cdot \mathbf{i} + \sin \psi \cos \theta \cdot \mathbf{j} - \sin \theta \cdot \mathbf{k}.} \] Следовательно, \[ {\frac{{\partial \mathbf{r}}}{{\partial \psi }} \times \frac{{\partial \mathbf{r}}}{{\partial \theta }} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ { - \sin \psi \sin \theta } & {\cos \psi \sin \theta } & 0\\ {\cos \psi \cos \theta } & {\sin \psi \cos \theta } & { - \sin \theta } \end{array}} \right|\; } = { - \cos \psi \,{\sin ^2}\theta \cdot \mathbf{i} - \sin \psi \,{\sin ^2}\theta \cdot \mathbf{j} } - {\left( {{{\sin }^2}\psi \sin \theta \cos \theta + {{\cos }^2}\psi \sin \theta \cos \theta } \right) \cdot \mathbf{k} } = { - \cos \psi \,{\sin ^2}\theta \cdot \mathbf{i} - \sin \psi \,{\sin ^2}\theta \cdot \mathbf{j} } - {\sin \theta \cos \theta \cdot \mathbf{k}.} \] Таким образом, получаем \[ {d\mathbf{S} } = {\left( { - \cos \psi \,{{\sin }^2}\theta , - \sin \psi \,{{\sin }^2}\theta , - \sin\theta \cos \theta } \right)d\psi d\theta .} \] (Этот вектор соответствует внутренней ориентации поверхности.) Находим поток векторного поля через заданную поверхность (или поверхностный интеграл второго рода): \[ {\iint\limits_S {\mathbf{F}\left( {r,\psi ,\theta } \right) \cdot d\mathbf{S}} } = {\iint\limits_{D\left( {\psi ,\theta } \right)} {\left[ {\left( { - \sin \psi \sin \theta } \right) \cdot \left( { - \cos \psi \,{{\sin }^2}\theta } \right)} \right.} } + {\cos \psi \sin \theta \cdot \left( { - \sin \psi \,{{\sin }^2}\theta } \right) } + {\left. {\left( { - \cos \theta } \right) \cdot \left( { - \cos \theta \sin \theta } \right)} \right]d\psi d\theta } = {\int\limits_{D\left( {\psi ,\theta } \right)} {\left[ {\sin \psi \cos \psi \,{{\sin }^3}\theta - \sin \psi \cos \psi \,{{\sin }^3}\theta } \right.} } {\left. { + \sin \theta \,{{\cos }^2}\theta } \right]d\psi d\theta } = {\int\limits_{D\left( {\psi ,\theta } \right)} {\sin \theta \,{{\cos }^2}\theta d\psi d\theta } } = {\int\limits_0^{2\pi } {d\psi } \int\limits_0^\pi {\sin \theta \,{{\cos }^2}\theta d\theta } } = { - 2\pi \int\limits_0^\pi {{{\cos }^2}\theta d\left( {\cos \theta } \right)} } = { - 2\pi \left[ {\left. {\left( {\frac{{{{\cos }^3}\theta }}{3}} \right)} \right|_0^\pi } \right] } = { - \frac{{2\pi }}{3}\left( {{{\cos }^3}\pi - {{\cos }^3}0} \right) } = {\frac{{4\pi }}{3}.} \]

   Пример 5

Вычислить интеграл \(\iint\limits_S {\large\frac{{dydz}}{x}\normalsize + \large\frac{{dzdx}}{y}\normalsize + \large\frac{{dxdy}}{z}\normalsize} ,\) где \(S\) − часть внутренней поверхности эллипсоида, заданного параметрически в виде \(\mathbf{r}\left( {u,v} \right) = \left( {a\cos u\cos v,b\sin u\cos v,c\sin v} \right).\) Параметры \(u, v\) изменяются в интервалах \(0 \le u \le 1,\) \(0 \le v \le \large\frac{\pi }{2}\normalsize.\) Воспользуемся формулой \[ {\iint\limits_S {Pdydz + Qdzdx + Rdxdy} } = {\iint\limits_{D\left( {u,v} \right)} {\left| {\begin{array}{*{20}{c}} P & Q & R\\ {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial z}}{{\partial u}}}\\ {\frac{{\partial x}}{{\partial v}}}&{\frac{{\partial y}}{{\partial v}}}&{\frac{{\partial z}}{{\partial v}}} \end{array}} \right|dudv} .} \] Поскольку \[\frac{{\partial x}}{{\partial u}} = \frac{\partial }{{\partial u}}\left( {a\cos u\cos v} \right) = - a\sin u\cos v,\] \[\frac{{\partial y}}{{\partial u}} = \frac{\partial }{{\partial u}}\left( {b\sin u\cos v} \right) = b\cos u\cos v,\] \[\frac{{\partial z}}{{\partial u}} = \frac{\partial }{{\partial u}}\left( {c\sin v} \right) = 0,\] \[\frac{{\partial x}}{{\partial v}} = \frac{\partial }{{\partial v}}\left( {a\cos u\cos v} \right) = - a\cos u\sin v,\] \[\frac{{\partial y}}{{\partial v}} = \frac{\partial }{{\partial v}}\left( {b\sin u\cos v} \right) = - b\sin u\sin v,\] \[\frac{{\partial z}}{{\partial v}} = \frac{\partial }{{\partial v}}\left( {c\sin v} \right) = c\cos v,\] то определитель можно записать в таком виде: \[ {\left| {\begin{array}{*{20}{c}} {\frac{1}{x}}&{\frac{1}{y}}&{\frac{1}{z}}\\ {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial z}}{{\partial u}}}\\ {\frac{{\partial x}}{{\partial v}}}&{\frac{{\partial y}}{{\partial v}}}&{\frac{{\partial z}}{{\partial v}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{1}{{a\cos u\cos v}}}&{\frac{1}{{b\sin u\cos v}}}&{\frac{1}{{c\sin v}}}\\ { - a\sin u\cos v}&{b\cos u\cos v}&0\\ { - a\cos u\sin v}&{ - b\sin u\sin v}&{c\cos v} \end{array}} \right| } = {\frac{1}{{a\cos u\cos v}} \cdot b\cos u\cos v \cdot c\cos v } + {\frac{1}{{b\sin u\cos v}} \cdot a\sin u\cos v \cdot c\cos v } + {\frac{1}{{c\sin v}} \cdot \left( {a\sin u\cos v \cdot b\sin u\sin v} \right. } + {\left. {a\cos u\sin v \cdot b\cos u\cos v} \right) } = {\frac{{bc}}{a}\cos v + \frac{{ac}}{b}\cos v + \frac{{ab}}{c}\left( {{{\sin }^2}u\cos v + {{\cos }^2}u\cos v} \right) } = {\left( {\frac{{ab}}{c} + \frac{{ac}}{b} + \frac{{bc}}{a}} \right)\cos v.} \] Следовательно, поверхностный интеграл равен \[ {I = \iint\limits_{D\left( {u,v} \right)} {\left( {\frac{{ab}}{c} + \frac{{ac}}{b} + \frac{{bc}}{a}} \right)\cos vdudv} } = {\left( {\frac{{ab}}{c} + \frac{{ac}}{b} + \frac{{bc}}{a}} \right)\int\limits_0^1 {du} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\cos vdv} } = {\left( {\frac{{ab}}{c} + \frac{{ac}}{b} + \frac{{bc}}{a}} \right) \cdot \left[ {\left. {\left( {\sin v} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{{ab}}{c} + \frac{{ac}}{b} + \frac{{bc}}{a}.} \]

   Пример 6

Найти интеграл \(\iint\limits_S {2xdydz},\) где \(S\) − внутренняя поверхность сферы \({x^2} + {y^2} + {z^2} = {a^2}.\) Запишем компоненты векторного поля \(\mathbf{F}:\) \[\mathbf{F}\left( {P,Q,R} \right) = \left( {2x,0,0} \right).\] Уравнение сферы удобно преобразовать в сферические координаты: \[ {\mathbf{r}\left( {\psi ,\theta } \right) } = {a\cos \psi \sin \theta \cdot \mathbf{i} + a\sin \psi \sin \theta \cdot \mathbf{j} + a\cos \theta \cdot \mathbf{k},} \] где \(0 \le \psi \le 2\pi ,\) \(0 \le \theta \le \pi.\) Применим формулу \[ {\iint\limits_S {Pdydz + Qdzdx + Rdxdy} } = {\iint\limits_{D\left( {\psi ,\theta } \right)} {\left| {\begin{array}{*{20}{c}} P&Q&R\\ {\frac{{\partial x}}{{\partial \psi }}}&{\frac{{\partial y}}{{\partial \psi }}}&{\frac{{\partial z}}{{\partial \psi }}}\\ {\frac{{\partial x}}{{\partial \theta }}}&{\frac{{\partial y}}{{\partial \theta }}}&{\frac{{\partial z}}{{\partial \theta }}} \end{array}} \right|d\psi d\theta } .} \] Так как \[\frac{{\partial x}}{{\partial \psi }} = \frac{\partial }{{\partial \psi }}\left( {a\cos \psi \sin \theta } \right) = - a\sin \psi \sin \theta ,\] \[\frac{{\partial y}}{{\partial \psi }} = \frac{\partial }{{\partial \psi }}\left( {a\sin \psi \sin \theta } \right) = a\cos \psi \sin \theta ,\] \[\frac{{\partial z}}{{\partial \psi }} = \frac{\partial }{{\partial \psi }}\left( {a\cos \theta } \right) = 0,\] \[\frac{{\partial x}}{{\partial \theta }} = \frac{\partial }{{\partial \theta }}\left( {a\cos \psi \sin \theta } \right) = a\cos \psi \cos \theta ,\] \[\frac{{\partial y}}{{\partial \theta }} = \frac{\partial }{{\partial \theta }}\left( {a\sin \psi \sin \theta } \right) = a\cos \psi \cos \theta ,\] \[\frac{{\partial z}}{{\partial \theta }} = \frac{\partial }{{\partial \theta }}\left( {a\cos \theta } \right) = - a\sin \theta ,\] то определитель под знаком двойного интеграла будет равен \[ {\left| {\begin{array}{*{20}{c}} P&Q&R\\ {\frac{{\partial x}}{{\partial \psi }}}&{\frac{{\partial y}}{{\partial \psi }}}&{\frac{{\partial z}}{{\partial \psi }}}\\ {\frac{{\partial x}}{{\partial \theta }}}&{\frac{{\partial y}}{{\partial \theta }}}&{\frac{{\partial z}}{{\partial \theta }}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {2a\cos \psi \sin \theta }&0&0\\ { - a\sin \psi \sin \theta }&{a\cos \psi \sin \theta }&0\\ {a\cos \psi \cos \theta }&{a\sin \psi \cos \theta }&{ - a\sin \theta } \end{array}} \right| } = {2a\cos \psi \sin \theta \cdot a\cos \psi \sin \theta \cdot \left( { - a\sin \theta } \right) } = { - 2{a^3}{\cos ^2}\psi \,{\sin ^3}\theta .} \] Это значение соответствует внутренней ориентации поверхности.

Искомый поверхностный интеграл будет равен \[ {I = 2\iint\limits_S {xdydz} } = { - 4\iint\limits_S {{a^3}{{\cos }^2}\psi \,{{\sin }^3}\theta d\psi d\theta } } = { - 4{a^3}\int\limits_0^{2\pi } {{{\cos }^2}\psi d\psi } \int\limits_0^\pi {{{\sin }^3}\theta d\theta } .} \] Вычислим последние два интеграла отдельно. \[ {\int\limits_0^{2\pi } {{{\cos }^2}\psi d\psi } } = {\frac{1}{2}\int\limits_0^{2\pi } {\left( {1 + \cos 2\psi } \right)d\psi } } = {\frac{1}{2}\left[ {\left. {\left( {\psi + \frac{{\sin 2\psi }}{2}} \right)} \right|_0^{2\pi }} \right] = \pi ,} \] \[ {\int\limits_0^\pi {{{\sin }^3}\theta d\theta } } = {\int\limits_0^\pi {{{\sin }^2}\theta \sin \theta d\theta } } = {\int\limits_0^\pi {\left( {{\cos^2}\theta - 1} \right)d\left( {\cos \theta } \right)} } = {\left. {\left( {\frac{{{\cos^3}\theta }}{3} - \cos \theta } \right)} \right|_0^\pi } = {\left( {\frac{{{\cos^3}\pi }}{3} - \cos \pi } \right) - \left( {\frac{{{\cos^3}0}}{3} - \cos 0} \right) } = {\left( { - \frac{1}{3} + 1} \right) - \left( {\frac{1}{3} - 1} \right) } = {\frac{4}{3}.} \] Следовательно, поверхностный интеграл имеет значение \[I = - 4{a^3} \cdot \pi \cdot \frac{4}{3} = - \frac{{16{a^3}\pi }}{3}.\]