Особые решения дифференциальных уравнений

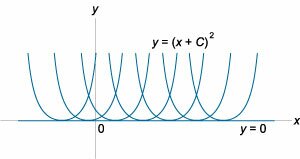
Функция \(\varphi \left( x \right)\) называется особым решением дифференциального уравнения \(F\left( {x,y,y'} \right) = 0,\) если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения. Геометрически это означает, что через каждую соответствующую точку \(\left( {{x_0},{y_0}} \right)\) проходит более одной интегральной кривой с общей касательной.

Примечание: Иногда используется более слабое определение особого решения, когда единственность решения нарушается лишь в некоторых точках.

Особое решение дифференциального уравнения не описывается общим интегралом. Поэтому, оно не выводится из общего решения ни при каком значении постоянной \(C.\) Это можно проиллюстрировать следующим примером:

Пусть требуется решить уравнение \({\left( {y'} \right)^2} - 4y = 0.\) Видно, что общее решение данного уравнения описывается функцией \(y = {\left( {x + C} \right)^2}.\) Графически общее решение представляется в виде семейства парабол (Рисунок \(1\)). Кроме этого, функция \(y = 0\) также удовлетворяет дифференциальному уравнению. Однако эта функция не содержится в общем решении! Поскольку через каждую точку прямой \(y = 0\) проходит более одной интегральной кривой, то единственность решения на этой прямой нарушается, и, следовательно, данная прямая является особым решением дифференциального уравнения. Одним из способов нахождения особого решения является исследование так называемого \(p\)-дискриминанта дифференциального уравнения. Если функция \(F\left( {x,y,y'} \right)\) и ее частные производные \({\large\frac{{\partial F}}{{\partial y}}\normalsize}, {\large\frac{{\partial F}}{{\partial y'}}\normalsize}\) непрерывны в области определения дифференциального уравнения, то особое решение находится из системы уравнений: \[\left\{ \begin{array}{l} F\left( {x,y,y'} \right) = 0\\ \frac{{\partial F\left( {x,y,y'} \right)}}{{\partial y'}} = 0 \end{array} \right..\] Уравнение \(\psi \left( {x,y} \right) = 0,\) которое получается при решении данной системы, называется \(p\)-дискриминантом дифференциального уравнения. Соответствующая кривая, определенная этим уравнением, называется \(p\)-дискриминантной кривой.

После нахождения \(p\)-дискриминантной кривой необходимо проверить следующее:

1. Является ли \(p\)-дискриминант решением дифференциального уравнения?

2. Является ли \(p\)-дискриминант особым решением, то есть существуют ли другие интегральные кривые дифференциального уравнения, которые касаются \(p\)-дискриминантной кривой в каждой точке?

Это можно сделать следующим образом:

• Сначала нужно найти общее решение дифференциального уравнения (обозначим его как \({y_1}\));

• Затем нужно записать условия касания кривой особого решения (обозначим его как \({y_2}\)) и семейства интегральных кривых общего решения \({y_1}\) в произвольной точке \({x_0}:\) \[\left\{ \begin{array}{l} {y_1}\left( {{x_0}} \right) = {y_2}\left( {{x_0}} \right)\\ {y'_1}\left( {{x_0}} \right) = {y'_2} \left( {{x_0}} \right) \end{array} \right.;\]

Если данная система имеет решение в произвольной точке \({x_0},\) то функция \({y_2}\) будет являться особым решением. Особое решение обычно соответствует огибающей семейства интегральных кривых общего решения дифференциального уравнения. Другой способ нахождения особого решения в виде огибающей семейства интегральных кривых основан на использовании \(C\)-дискриминанта.

Пусть \(\Phi \left( {x,y,C} \right)\) является общим решением дифференциального уравнения \(F\left( {x,y,y'} \right) = 0.\) Графически уравнение \(\Phi \left( {x,y,C} \right) = 0\) соответствует семейству интегральных кривых на плоскости \(xy.\) Если функция \(\Phi \left( {x,y,C} \right)\) и ее частные производные непрерывны, то огибающая семейства интегральных кривых общего решения определяется системой уравнений: \[\left\{ \begin{array}{l} \Phi \left( {x,y,C} \right) = 0\\ \frac{{\partial \Phi \left( {x,y,C} \right)}}{{\partial C}} = 0 \end{array} \right..\] Чтобы убедиться, что решение данной системы уравнений действительно является огибающей, можно воспользоваться методом, рассмотренным в предыдущем пункте. Более общий способ нахождения особых точек дифференциального уравнения основан на одновременном использовании \(p\)-дискриминанта и \(C\)-дискриминанта.

Сначала мы определяем уравнения \(p\)-дискриминанта и \(C\)-дискриминанта:

• \({\psi_p}\left( {x,y} \right) = 0\) − уравнение \(p\)-дискриминанта;

• \({\psi_C}\left( {x,y} \right) = 0\) − уравнение \(C\)-дискриминанта.

Оказывается, что эти уравнения имеют определенную структуру. В общем случае, уравнение \(p\)-дискриминанта представляется в виде произведения трех функций: \[{\psi _p}\left( {x,y} \right) = E \times {T^2} \times C = 0,\] где \(E\) означает уравнение огибающей, \(T\) − уравнение точек прикосновения и \(C\) − уравнение точек заострения.

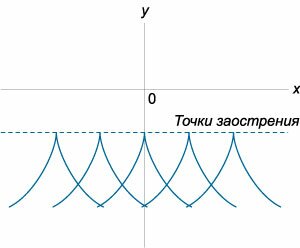
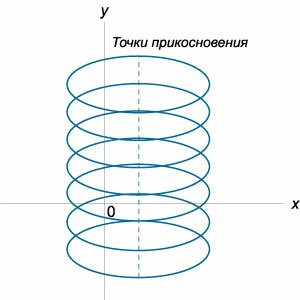
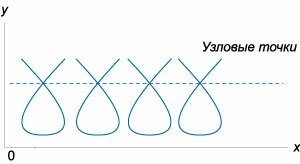
Аналогично, уравнение \(C\)-дискриминанта также раскладывается на произведение трех функций: \[{\psi _C}\left( {x,y} \right) = E \times {N^2} \times {C^3} = 0,\] где \(E\) − уравнение огибающей, \(N\) − уравнение узловых точек, а \(C\) − уравнение точек заострения.

Здесь мы имеем дело с новыми типами особых точек: \(C\) - точки заострения, \(T\) - точки прикосновения и \(N\) - узловые точки. Их вид в плоскости \(xy\) схематически представлен на рисунках \(2-4.\) Три типа особых точек из четырех, а именно: точки заострения, точки прикосновения и узловые точки, − являются внешними, то есть они не удовлетворяют дифференциальному уравнению и, поэтому, не являются особыми решениями дифференциального уравнения. Только уравнение огибающей будет являться особым решением. Поскольку огибающая входит в уравнения обоих дискриминантов в виде множителя в первой степени, то ее уравнение легко определяется из данной системы.

   Пример 1

Найти особые решения уравнения \(1 + {\left( {y'} \right)^2} = {\large\frac{1}{{{y^2}}}\normalsize}.\) Будем использовать \(p\)-дискриминант для исследования особых точек. Дифференцируя заданное уравнение по производной \(y',\) получаем: \[2y' = 0,\;\; \Rightarrow y' = 0.\] Подставляя это в дифференциальное уравнение, находим уравнение \(p\)-дискриминанта: \[1 + 0 = \frac{1}{{{y^2}}}.\] Отсюда следует, что уравнение \(p\)-дискриминанта описывает две горизонтальных прямые: \(y = \pm 1.\) Легко проверить, что это решение удовлетворяет дифференциальному уравнению: \[ {y = \pm 1,\;\; \Rightarrow y' = 0,}\;\; {\Rightarrow 1 + {0^2} = \frac{1}{{{1^2}}},}\;\; {\Rightarrow 1 = 1.} \] Теперь определим общее решение дифференциального уравнения. Мы можем записать его в следующей форме: \[ {{\left( {y'} \right)^2} = \frac{1}{{{y^2}}} - 1 = \frac{{1 - {y^2}}}{{{y^2}}},}\;\; {\Rightarrow y' = \pm \frac{{\sqrt {1 - {y^2}} }}{y},}\;\; {\Rightarrow \frac{{ydy}}{{\sqrt {1 - {y^2}} }} = \pm dx.} \] Сделаем замену: \[ {1 - {y^2} = t,\;\; \Rightarrow - 2ydy = dt,}\;\; {\Rightarrow ydy = - \frac{{dt}}{2}.} \] В результате имеем: \[\frac{{\left( { - \frac{{dt}}{2}} \right)}}{{\sqrt t }} = \pm dx.\] После интегрирования получаем общее решение дифференциального уравнения: \[ {\int {\frac{{dt}}{{2\sqrt t }}} = \pm \int {dx} ,}\;\; {\Rightarrow \sqrt t = \pm x + C,}\;\; {\Rightarrow \sqrt {1 - {y^2}} = \pm \left( {x + C} \right),} \] где \(C\) − произвольная постоянная.

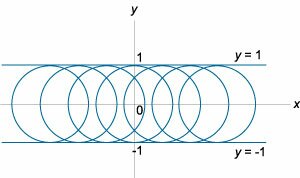
Последнее выражение можно записать в следующем виде: \[{\left( {x + C} \right)^2} + {y^2} = 1.\] Это уравнение описывает семейство окружностей радиусом \(1,\) заполняющих полосу \(-1 \le y \le 1\) (рисунок \(5\)). Как видно из рисунка, прямые линии \(p\)-дискриминанта \(y = \pm 1\) являются огибающими для данного семейства окружностей. Однако необходимо формально проверить, что на этих прямых нарушается единственность решения.

Возьмем произвольную точку \({x_0}.\) Запишем условие касания двух интегральных кривых в этой точке: \[ \left\{ \begin{array}{l} {y_1}\left( {{x_0}} \right) = {y_2}\left( {{x_0}} \right)\\ {y'_1}\left( {{x_0}} \right) = {y'_2} \left( {{x_0}} \right) \end{array} \right.. \] Здесь через \({y_1}\left( x \right)\) обозначено общее решение, которое для верхней полуокружности имеет вид: \[{y_1}\left( x \right) = \sqrt {1 - {{\left( {x + C} \right)}^2}} .\] Функция \({y_2}\left( x \right)\) соответствует горизонтальной прямой \(y = 1.\) Обе кривые будут соприкасаться в точке \({x_0},\) если выполняются следующие условия: \[\left\{ \begin{array}{l} \sqrt {1 - {{\left( {{x_0} + C} \right)}^2}} = 1\\ \frac{{ - {x_0} - C}}{{\sqrt {1 - {x_0} + C} }} = 0 \end{array} \right..\] Эти условия будут удовлетворяться, если положить \(C = - {x_0}.\)

Таким образом, мы доказали, что в каждой точке \({x_0}\) прямой линии \(y = 1\) существует касательная окружность с параметром \(C = - {x_0}.\) Следовательно, единственность решения нарушается в каждой точке прямой линии. Поэтому, прямая \(y = 1\) является особым решением заданного дифференциального уравнения. Аналогично можно доказать, что прямая \(y = -1\) также будет являться особым решением.

   Пример 2

Найти особое решение дифференциального уравнения \(y = {\left( {y'} \right)^2} - 3xy' + 3{x^2}.\) Общее решение данного уравнения известно и определяется функцией \(y = Cx + {C^2} + {x^2}.\) Будем использовать \(С\)-дискриминант для нахождения особого решения. Поскольку общее решение дифференциального уравнения известно, то можно записать: \[\Phi \left( {x,y,C} \right) = y - Cx - {C^2} - {x^2}.\] Частная производная по \(C\) имеет вид: \[\frac{{\partial \Phi \left( {x,y,C} \right)}}{{\partial C}} = - x - 2C.\] В результате получаем следующую систему уравнений: \[\left\{ \begin{array}{l} y = Cx - {C^2} - {x^2}\\ - x - 2C = 0 \end{array} \right..\] Из второго уравнения следует, что \(C = - \large\frac{x}{2}\normalsize.\) Подставляя это в первое уравнение, находим \(C\)-дискриминантную кривую, которая является параболой: \[ {y = \left( { - \frac{x}{2}} \right) \cdot x - {\left( { - \frac{x}{2}} \right)^2} - {x^2} } = {\frac{3}{4}{x^2}.} \] Убедимся, что эта функция действительно будет одним из решений исходного дифференциального уравнения: \[ {y = \frac{3}{4}{x^2},}\;\; {\Rightarrow y' = \frac{3}{2}x,}\;\; {\Rightarrow \frac{3}{4}{x^2} = {\left( {\frac{3}{2}x} \right)^2} - 3x \cdot \frac{3}{2}x + 3{x^2},}\;\; {\Rightarrow \frac{3}{4}{x^2} = \frac{9}{4}{x^2} - \frac{9}{2}{x^2} + 3{x^2},}\;\; {\Rightarrow \frac{3}{4}{x^2} = \frac{3}{4}{x^2}.} \] Теперь проверим, что на этой кривой нарушается единственность решения. Обозначим \[{y_1} = Cx + {C^2} + {x^2},\;\;{y_2} = \frac{3}{4}{x^2}.\] Запишем условия касания двух кривых в некоторой произвольной точке \({x_0}:\) \[ \left\{ \begin{array}{l} {y_1}\left( {{x_0}} \right) = {y_2}\left( {{x_0}} \right)\\ {y'_1}\left( {{x_0}} \right) = {y'_2} \left( {{x_0}} \right) \end{array} \right.. \] В результате имеем: \[\left\{ \begin{array}{l} C{x_0} + {C^2} + x_0^2 = \frac{3}{4}x_0^2\\ C + 2{x_0} = \frac{3}{2}{x_0} \end{array} \right..\] Данная система уравнений совместна, если постоянная \(C\) в каждой точке \({x_0}\) равна \[C = - \frac{{{x_0}}}{2}.\] Таким образом, мы доказали, что \(C\)-дискриминантная кривая \(y = {\large\frac{3}{4}\normalsize}{x^2}\) является огибающей (т.е. особым решением) для семейства парабол \(y = Cx + {C^2} + {x^2},\) представляющих общее решение дифференциального уравнения.

   Пример 3

Исследовать особые решения дифференциального уравнения \({\left( {y'} \right)^2}{\left( {1 - y} \right)^2} = 2 - y.\) Сначала найдем \(p\)-дискриминант данного уравнения. Дифференцируя уравнение по \(x,\) получаем: \[2y'{\left( {1 - y} \right)^2} = 0.\] Исключим производную \(y'\) из системы уравнений \[\left\{ \begin{array}{l} {\left( {y'} \right)^2}{\left( {1 - y} \right)^2} = 2 - y\\ y'{\left( {1 - y} \right)^2} = 0 \end{array} \right..\] В результате имеем: \[ {{\left( {y'} \right)^2} = \frac{{2 - y}}{{{{\left( {1 - y} \right)}^2}}},}\;\; {\Rightarrow \frac{{2 - y}}{{{{\left( {1 - y} \right)}^2}}} \cdot {\left( {1 - y} \right)^4} = 0,}\;\; {\Rightarrow {\left( {1 - y} \right)^2}\left( {2 - y} \right) = 0.} \] Теперь определим \(C\)-дискриминант. К сожалению, для этого необходимо найти общее решение дифференциального уравнения :(. Перепишем уравнение в следующем виде: \[ {{\left( {\frac{{dy}}{{dx}}} \right)^2} = \frac{{2 - y}}{{{{\left( {1 - y} \right)}^2}}},}\;\; {\Rightarrow \frac{{dy}}{{dx}} = \pm \frac{{\sqrt {2 - y} }}{{1 - y}},}\;\; {\Rightarrow \frac{{\left( {1 - y} \right)dy}}{{\sqrt {2 - y} }} = \pm dx.} \] Интегрируем обе части: \[\int {\frac{{\left( {1 - y} \right)dy}}{{\sqrt {2 - y} }}} = \pm \int {dx} + C.\] В левом интеграле сделаем замену переменной: \[ {2 - y = t,\;\; \Rightarrow dy = - dt,}\;\; {\Rightarrow 1 - y = t - 1.} \] В результате получаем: \[ {\int {\frac{{\left( {t - 1} \right)\left( { - dt} \right)}}{{\sqrt t }}} = \pm x + C,}\;\; {\Rightarrow \int {\left( {\sqrt t - \frac{1}{{\sqrt t }}} \right)dt} = \mp x - C,}\;\; {\Rightarrow \frac{{{t^{\large\frac{3}{2}\normalsize}}}}{{\frac{3}{2}}} - \frac{{{t^{\large\frac{1}{2}\normalsize}}}}{{\frac{1}{2}}} = \mp x - C,}\;\; {\Rightarrow \frac{2}{3}{t^{\large\frac{3}{2}\normalsize}} - 2{t^{\large\frac{1}{2}\normalsize}} = \mp x - C,}\;\; {\Rightarrow \frac{2}{3}{\left( {2 - y} \right)^{\large\frac{3}{2}\normalsize}} - 2{\left( {2 - y} \right)^{\large\frac{1}{2}\normalsize}} = \mp x - C,}\;\; {\Rightarrow \frac{2}{3}\sqrt {2 - y} \left( {2 - y - 3} \right) = \mp x - C,}\;\; {\Rightarrow \frac{4}{9}\left( {2 - y} \right){\left( {y + 1} \right)^2} = {\left( {x + C} \right)^2},}\;\; {\Rightarrow 4\left( {2 - y} \right){\left( {y + 1} \right)^2} = 9{\left( {x + C} \right)^2}.} \] Дифференцируем общее решение по \(C:\) \[0 = 18\left( {x + C} \right).\] Подставляя \(x + C = 0\) снова в общее решение, находим уравнение \(C\)-дискриминанта: \[{\left( {y + 1} \right)^2}\left( {2 - y} \right) = 0.\] Теперь запишем вместе уравнения обоих дискриминантов: \[{\psi _p}\left( y \right) = {\left( {1 - y} \right)^2}\left( {2 - y} \right) = 0,\] \[{\psi _C}\left( y \right) = {\left( {y + 1} \right)^2}\left( {2 - y} \right) = 0.\] Из структуры уравнений дискриминантов следует, что \(2 - y = 0\) является уравнением огибающей, поскольку это выражение содержится в обоих дискриминантах в первой степени.

Из выражения для \(p\)-дискриминанта можно также определить уравнение точек прикосновения: \[{\left( {1 - y} \right)^2} = 0,\;\; \Rightarrow y = 1.\] Аналогично, из формулы для \(C\)-дискриминанта находим уравнение узловых точек: \[{\left( {y + 1} \right)^2} = 0,\;\; \Rightarrow y = - 1.\] В данном примере лишь огибающая \(y = 2\) будет являться особым решением дифференциального уравнения.