Определенный интеграл. Формула Ньютона-Лейбница.

Пусть функция \(f\left( x \right)\) непрерывна на замкнутом интервале \(\left[ {a,b} \right].\) Разобьем данный отрезок на \(n\) частичных интервалов. В каждом интервале выберем произвольную точку \({\xi_i}\) и составим интегральную сумму \(\sum\limits_{i = 1}^n {f\left( {{\xi _i}} \right)\Delta {x_i}} \), где \(\Delta {x_i}\) − длина \(i\)-го интервала. Определенный интеграл от функции \(f\left( x \right)\) в пределах от \(a\) до \(b\) вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю: \[\require{AMSmath.js} \int\limits_a^b {f\left( x \right)dx} = \lim\limits_{\substack{ n \to \infty \\ \text{max}\,\Delta {x_i} \to 0}} \sum\limits_{i = 1}^n {f\left( {{\xi _i}} \right)\Delta {x_i}} ,\] где \(\Delta {x_i} = {x_i} - {x_{i - 1}},\) \({x_{i - 1}} \le {\xi _i} \le {x_i}.\) Ниже предполагается, что \(f\left( x \right)\) и \(g\left( x \right)\) - непрерывные функции на замкнутом интервале \(\left[ {a,b} \right].\)

1. \(\int\limits_a^b {1dx} = b - a\)

2. \(\int\limits_a^b {kf\left( x \right)dx} = k \int\limits_a^b {f\left( x \right)dx} ,\;\) где \(k\) - константа;

3. \( {\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} } = {\int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} } \)

4. \( {\int\limits_a^b {f\left( x \right)dx} } = {\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} ,\;}\) где \(a < c < b;\)

5. Если \(0 \le f\left( x \right) \le g\left( x \right)\) для всех \(x \in \left[ {a,b} \right],\) то \(0 \le \int\limits_a^b {f\left( x \right)dx} \le \int\limits_a^b {g\left( x \right)dx} .\)

6. \(\int\limits_a^a {f\left( x \right)dx} = 0\)

7. \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx}\)

8. Если \(f\left( x \right) \ge 0\) в интервале \(\left[ {a,b} \right],\) то \(\int\limits_a^b {f\left( x \right)dx} \ge 0\)

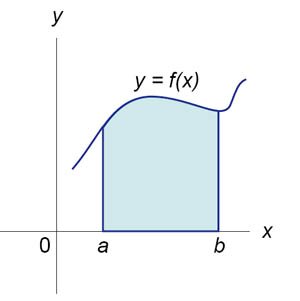
Пусть функция \(f\left( x \right)\) непрерывна на замкнутом интервале \(\left[ {a,b} \right].\) Если \(F\left( x \right)\) - первообразная функции \(f\left( x \right)\) на \(\left[ {a,b} \right],\) то \[ {\int\limits_a^b {f\left( x \right)dx} } = {\left. 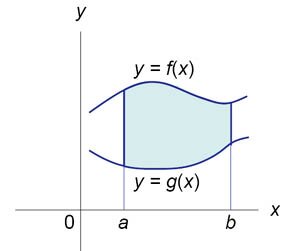{F\left( x \right)} \right|_a^b } = {F\left( b \right) - F\left( a \right).} \] Площадь фигуры, ограниченной осью \(Ox,\) двумя вертикальными прямыми \(x = a,\) \(x = b\) и графиком функции \(f\left( x \right)\) (рисунок \(1\)), определяется по формуле \[S = \int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right).\] Пусть \(F\left( x \right)\) и \(G\left( x \right)\) - первообразные функций \(f\left( x \right)\) и \(g\left( x \right),\) соответственно. Если \(f\left( x \right) \ge g\left( x \right)\) на замкнутом интервале \(\left[ {a,b} \right],\) то площадь области, ограниченной двумя кривыми \(y = f\left( x \right),\) \(y = g\left( x \right)\) и вертикальными линиями \(x = a,\) \(x = b\) (рисунок \(2\)), определяется формулой \[ {S = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } = {F\left( b \right) - G\left( b \right) - F\left( a \right) + G\left( a \right).} \] Определенный интеграл \(\int\limits_a^b {f\left( x \right)dx} \) по переменной \(x\) можно преобразовать в определенный интеграл относительно переменной \(t\) с помощью подстановки \(x = g\left( t \right):\) \[\int\limits_a^b {f\left( x \right)dx} = \int\limits_c^d {f\left( {g\left( t \right)} \right)g'\left( t \right)dt} .\] Новые пределы интегрирования по переменной \(t\) определяются выражениями \[c = {g^{ - 1}}\left( a \right),\;\;d = {g^{ - 1}}\left( b \right),\] где \({g^{ - 1}}\) − обратная функция к \(g,\) т.е. \(t = {g^{ - 1}}\left( x \right).\)


В этом случае формула интегрирования по частям имеет вид: \[\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} ,\] где \(\left. {uv} \right|_a^b\) означает разность значений произведения функций \(uv\) при \(x = b\) и \(x = a.\)

   Пример 1

Вычислить интеграл \(\int\limits_0^2 {\left( {{x^3} - {x^2}} \right)dx} .\) Применяя формулу Ньютона-Лейбница, получаем \[ {\int\limits_0^2 {\left( {{x^3} - {x^2}} \right)dx} } = {\left. {\left( {\frac{{{x^4}}}{4} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 } = {\left( {\frac{{16}}{4} - \frac{8}{3}} \right) - 0 = \frac{4}{3}.} \]

   Пример 2

Вычислить интеграл \(\int\limits_0^1 {\left( {\sqrt[\large 3\normalsize]{t} - \sqrt t } \right)dt} .\) \[ {\int\limits_0^1 {\left( {\sqrt[\large 3\normalsize]{t} - \sqrt t } \right)dt} } = {\int\limits_0^1 {\left( {{t^{\large\frac{1}{3}\normalsize}} - {t^{\large\frac{1}{2}\normalsize}}} \right)dt} } = {\left. {\left( {\frac{{{t^{\large\frac{1}{3}\normalsize + 1}}}}{{\frac{1}{3} + 1}} - \frac{{{t^{\large\frac{1}{2}\normalsize + 1}}}}{{\frac{1}{2} + 1}}} \right)} \right|_0^1 } = {\left. {\left( {\frac{{3{t^{\large\frac{4}{3}\normalsize}}}}{4} - \frac{{2{t^{\large\frac{3}{2}\normalsize}}}}{3}} \right)} \right|_0^1 } = {\left( {\frac{3}{4} - \frac{2}{3}} \right) - 0 = \frac{1}{{12}}.} \]

   Пример 3

Вычислить интеграл \(\int\limits_0^1 {{\large\frac{x}{{{{\left( {3{x^2} - 1} \right)}^4}}}\normalsize} dx}.\) Сделаем замену: \[ {t = 3{x^2} - 1,}\;\; {\Rightarrow dt = 6xdx,}\;\; {\Rightarrow xdx = \frac{{dt}}{6}.} \] Пересчитаем пределы интегрирования. Если \(x = 0,\) то \(t = -1.\) Если же \(x = 1,\) то \(t = 2.\) Тогда интеграл через новую переменную \(t\) легко вычисляется: \[ {\int\limits_0^1 {\frac{x}{{{{\left( {3{x^2} - 1} \right)}^4}}}dx} } = {\int\limits_{ - 1}^2 {\frac{{\frac{{dt}}{6}}}{{{t^4}}}} } = {\frac{1}{6}\int {{t^{ - 4}}dt} } = {\frac{1}{6}\left. {\left( {\frac{{{t^{ - 3}}}}{{ - 3}}} \right)} \right|_{ - 1}^2 } = { - \frac{1}{{18}}\left( {\frac{1}{8} - 1} \right) } = {\frac{7}{{144}}.} \]

   Пример 4

Вычислить интеграл \(\int\limits_0^{\ln 2} {x{e^{ - x}}dx}.\) Запишем интеграл в виде \[ {I = \int\limits_0^{\ln 2} {x{e^{ - x}}dx} } = { - \int\limits_0^{\ln 2} {xd\left( {{e^{ - x}}} \right)} .} \] Используем интегрирование по частям: \({\large\int\normalsize} {udv} = uv - {\large\int\normalsize} {vdu} .\) В нашем случае пусть будет \[ {u = x,\;\;dv = d\left( {{e^{ - x}}} \right),}\;\; {\Rightarrow du = 1,\;\;v = {e^{ - x}}.} \] Следовательно, интеграл равен \[ {I = - \int\limits_0^{\ln 2} {xd\left( {{e^{ - x}}} \right)} } = { - \left[ {\left. {\left( {x{e^{ - x}}} \right)} \right|_0^{\ln 2} - \int\limits_0^{\ln 2} {{e^{ - x}}dx} } \right] } = { - \left. {\left( {x{e^{ - x}}} \right)} \right|_0^{\ln 2} + \int\limits_0^{\ln 2} {{e^{ - x}}dx} } = { - \left. {\left( {x{e^{ - x}}} \right)} \right|_0^{\ln 2} - \left. {\left( {{e^{ - x}}} \right)} \right|_0^{\ln 2} } = { - \left. {\left[ {{e^{ - x}}\left( {x + 1} \right)} \right]} \right|_0^{\ln 2} } = { - {e^{ - \ln 2}}\left( {\ln 2 + 1} \right) + {e^0} \cdot 1 } = { - \frac{{\ln 2}}{2} - \frac{{\ln e}}{2} + \ln e } = {\frac{{\ln e}}{2} - \frac{{\ln 2}}{2} } = {\frac{1}{2}\left( {\ln e - \ln 2} \right) } = {\frac{1}{2}\ln \frac{e}{2}.} \]

   Пример 5

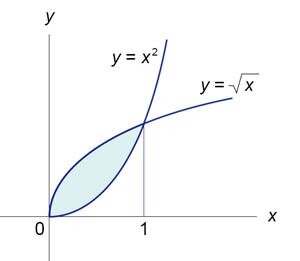
Найти площадь фигуры, ограниченной кривыми \(y = {x^2}\) и \(y = \sqrt x .\) Сначала определим точки пересечения двух кривых (рисунок \(3\)). \[ {{x^2} = \sqrt x ,}\;\; {\Rightarrow {x^2} - \sqrt x = 0,}\;\; {\Rightarrow \sqrt x \left( {{x^{\large\frac{3}{2}\normalsize}} - 1} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = 1.} \] Таким образом, данные кривые пересекаются в точках \(\left( {0,0} \right)\) и \(\left( {1,1}\right).\) Следовательно, площадь фигуры равна \[ {S = \int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)dx} } = {\left. {\left( {\frac{{{x^{\large\frac{1}{2}\normalsize + 1}}}}{{\frac{1}{2} + 1}} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 } = {\frac{1}{3}\left. {\left( {2\sqrt {{x^3}} - {x^3}} \right)} \right|_0^1 = \frac{1}{3}.} \]

   Пример 6

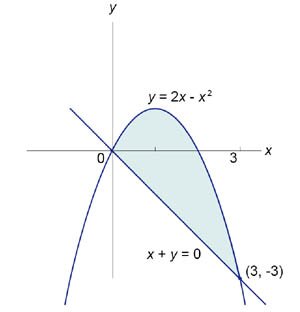
Найти площадь фигуры, ограниченную графиками функций \(y = 2x - {x^2}\) и \(x + y = 0.\) Найдем координаты точек пересечения кривых (рисунок \(4\)). \[ {2x - {x^2} = - x,}\;\; {\Rightarrow {x^2} - 3x = 0,}\;\; {\Rightarrow x\left( {x - 3} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = 3.} \] Данная область ограничивается сверху параболой \(y = 2x - {x^2},\) а снизу − прямой линией \(y = -x.\) Следовательно, площадь этой области равна \[ {S = \int\limits_0^3 {\left[ {2x - {x^2} - \left( { - x} \right)} \right]dx} } = {\int\limits_0^3 {\left( {2x - {x^2} + x} \right)dx} } = {\left. {\left( {{x^2} - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right)} \right|_0^3 } = {\left. {\left( {\frac{{3{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)} \right|_0^3 } = {\frac{{27}}{2} - \frac{{27}}{3} = \frac{9}{2}.} \]

   Пример 7

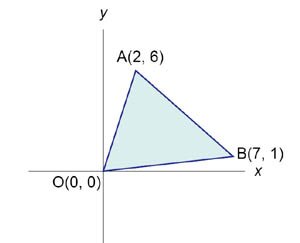
Найти площадь треугольника с вершинами в точках \(\left( {0,0} \right),\) \(\left( {2,6} \right)\) и \(\left( {7,1} \right).\) Найдем сначала уравнение стороны \(OA\) (рисунок \(5\)). \[ {\frac{{x - {x_O}}}{{{x_A} - {x_O}}} = \frac{{y - {y_O}}}{{{y_A} - {y_O}}},}\;\; {\Rightarrow \frac{{x - 0}}{{2 - 0}} = \frac{{y - 0}}{{6 - 0}},}\;\; {\Rightarrow \frac{x}{2} = \frac{y}{6},}\;\; {\Rightarrow y = 3x.} \] Аналогично, получим уравнение стороны \(OB.\) \[ {\frac{{x - {x_O}}}{{{x_B} - {x_O}}} = \frac{{y - {y_O}}}{{{y_B} - {y_O}}},}\;\; {\Rightarrow \frac{{x - 0}}{{7 - 0}} = \frac{{y - 0}}{{1 - 0}},}\;\; {\Rightarrow \frac{x}{7} = \frac{y}{1},}\;\; {\Rightarrow y = \frac{x}{7}.} \] Наконец, найдем уравнение третьей стороны \(AB.\) \[ {\frac{{x - {x_B}}}{{{x_A} - {x_B}}} = \frac{{y - {y_B}}}{{{y_A} - {y_B}}},}\;\; {\Rightarrow \frac{{x - 2}}{{7 - 2}} = \frac{{y - 6}}{{1 - 6}},}\;\; {\Rightarrow \frac{{x - 2}}{5} = \frac{{y - 6}}{{ - 5}},}\;\; {\Rightarrow y = 8 - x.} \] Как видно из рисунка \(5,\) площадь треугольника равна сумме двух интегралов: \[ {S = {I_1} + {I_2} } = {\int\limits_0^2 {\left( {3x - \frac{x}{7}} \right)dx} + \int\limits_2^7 {\left( {8 - x - \frac{x}{7}} \right)dx} } = {\left. {\left( {\frac{{10{x^2}}}{7}} \right)} \right|_0^2 + \left. {\left( {8x - \frac{{4{x^2}}}{7}} \right)} \right|_2^7 } = {\frac{{10 \cdot 4}}{7} + \left( {56 - \frac{{4 \cdot 49}}{7}} \right) - \left( {16 - \frac{{4 \cdot 4}}{7}} \right) = 20.} \]

   Пример 8

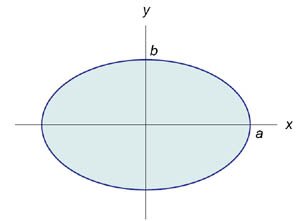
Вычислить площадь эллипса \({\large\frac{{{x^2}}}{{{a^2}}}\normalsize} + {\large\frac{{{y^2}}}{{{b^2}}}\normalsize} = 1.\) В силу симметрии (см. рисунок \(6\)), достаточно вычислить площадь полуэллипса, расположенного выше оси \(Ox,\) и затем результат умножить на \(2.\) Площадь полуэллипса равна \[ {{S_{\frac{1}{2}}} = \int\limits_{ - a}^a {\sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} dx} } = {\frac{b}{a}\int\limits_{ - a}^a {\sqrt {{a^2} - {x^2}} dx} .} \] Для вычисления данного интеграла используем тригонометрическую подстановку \(x = a\sin t,\) \(dx = a\cos tdt.\) Уточним пределы интегрирования. Если \(x = -a,\) то \(\sin t = -1\) и \(t = - \large\frac{\pi }{2}\normalsize.\) Если \(x = a,\) то \(\sin t = 1\) и \(t = \large\frac{\pi }{2}\normalsize.\) Таким образом, мы получаем \[ {{S_{\frac{1}{2}}} = \frac{b}{a}\int\limits_{ - a}^a {\sqrt {{a^2} - {x^2}} dx} } = {\frac{b}{a}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\sqrt {{a^2} - {a^2}{{\sin }^2}t}\,a\cos tdt} } = {ab\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {{{\cos }^2}tdt} } = {ab\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\frac{{1 + \cos 2t}}{2}dt} } = {\frac{{ab}}{2}\int\limits_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} {\left( {1 + \cos 2t} \right)dt} } = {\frac{{ab}}{2}\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_{ - \large\frac{\pi }{2}\normalsize}^{\large\frac{\pi }{2}\normalsize} } = {\frac{{ab}}{2}\left[ {\frac{\pi }{2} + \frac{{\sin \pi }}{2} - \left( { - \frac{\pi }{2}} \right) - \frac{{\sin \left( { - \pi } \right)}}{2}} \right] } = {\frac{{\pi ab}}{2}.} \] Следовательно, полная площадь эллипса равна \(\pi ab.\)