Определение предела функции

Пусть функция \(f\left( x \right)\) определена на некотором открытом интервале \(X\), содержащем точку \(x = a\). (При этом не требуется, чтобы значение \(f\left( a \right)\) было обязательно определено.)

Число \(L\) называется пределом функции \(f\left( x \right)\) при \(x \to a\), если для каждого \(\varepsilon > 0\) существует такое число \(\delta > 0\), что \[\left| {f\left( x \right) - L} \right| < \varepsilon ,\] при условии \[0 < \left| {x - a} \right| < \delta .\] Данное определение предела известно как \(\varepsilon-\delta-\) определение или определение Коши.

Существует также определение предела функции по Гейне, согласно которому функция \(f\left( x \right)\) имеет предел \(L\) в точке \(x = a\), если для каждой последовательности \(\left\{ {{x_n}} \right\}\), сходящейся к точке \(a\), последовательность \(f\left( {{x_n}} \right)\) сходится к \(L\). Определения предела функции по Коши и Гейне эквивалентны.

Символом \(\lim\limits_{x \to a - 0} \) обозначается левосторонний предел, в котором переменная \(x\), приближаясь к \(a\), принимает значения \(x < a\). Соответствующий предел \(\lim\limits_{x \to a - 0} f\left( x \right)\) называется левосторонним пределом функции \(f\left( x \right)\) в точке \(x = a\).

Аналогично, символом \(\lim\limits_{x \to a + 0} \) обозначается правосторонний предел, в котором переменная \(x\), приближаясь к \(a\), принимает значения \(x > a\). Соответствующий предел \(\lim\limits_{x \to a + 0} f\left( x \right)\) называется правосторонним пределом функции \(f\left( x \right)\) в точке \(x = a\).

Отметим, что двусторонний предел \(\lim\limits_{x \to a} f\left( x \right)\) существуют лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть \(\lim\limits_{x \to a - 0}f\left( x \right) = \lim\limits_{x \to a + 0}f\left( x \right) \). В этом случае \[\lim\limits_{x \to a}f\left( x \right) = \lim\limits_{x \to a - 0}f\left( x \right) = \lim\limits_{x \to a + 0}f\left( x \right).\]

   Пример 1

Используя \(\varepsilon-\delta-\) определение предела, показать что \(\lim\limits_{x \to 3} \left( {3x - 2} \right) = 7\). Пусть \(\varepsilon > 0\) является произвольным положительным числом. Выберем \(\delta = \large\frac{\varepsilon }{3}\normalsize\). Очевидно, что если \[0 < \left| {x - 3} \right| < \delta, \] то \[\left| {f\left( x \right) - L} \right| = \left| {\left( {3x - 2} \right) - 7} \right| = \left| {3x - 9} \right| ={ 3\left| {x - 3} \right| < 3\delta = 3 \cdot \frac{\varepsilon }{3} = \varepsilon .} \] Данный предел доказан в соответствии с определением Коши.

   Пример 2

Используя \(\varepsilon-\delta-\) определение предела, показать что \(\lim\limits_{x \to 2} {x^2} = 4\). Положим для простоты, что \(\delta = 1\), т.е. \[\left| {x - 2} \right| < 1.\] Пусть \(\varepsilon > 0\) является произвольным положительным числом. Тогда можно записать следующее неравенство: \[\left| {{x^2} - 4} \right| < \varepsilon ,\;\; {\Rightarrow \left| {x - 2} \right|\left| {x + 2} \right| < \varepsilon ,\;\; } {\Rightarrow \left| {x - 2} \right|\left( {x + 2} \right) < \varepsilon .} \] Так как максимальное значение \(x\) равно 3 (в соответствии с выбранным выше значением \(\delta\) ), то получаем \[5\left| {x - 2} \right| < \varepsilon \;\;(\text{если } \left| {x - 2} \right| < 1),\; {\text{или}\;\left| {x - 2} \right| < \frac{\varepsilon }{2}.} \] Тогда для любого произвольного числа \(\varepsilon > 0\) мы можем выбрать число \(\delta\) такое, что \[\delta = \min \left( {\frac{\varepsilon }{2},1} \right).\] В результате неравенства в определении предела будут выполнены. Искомый предел доказан.

   Пример 3

Используя \(\varepsilon-\delta-\) определение предела, найти значение \(\delta\), соответствующее заданному числу \(\varepsilon\) для следующего предела \[\lim\limits_{x \to 7} \sqrt {x + 2} = 3,\;\;\varepsilon = 0.2\] В соответствии с определением предела можно записать \[\left| {f\left( x \right) - 3} \right| < \varepsilon ,\;\text{если}\;\left| {x - 7} \right| < \delta .\] Подставляя \({f\left( x \right)}\) и \(\varepsilon\), получаем \[ {\left| {\sqrt {x + 2} - 3} \right| < 0.2,}\;\; {\Rightarrow - 0.2 < \sqrt {x + 2} - 3 < 0.2,} \;\; {\Rightarrow 3 - 0.2 < \sqrt {x + 2} < 3 + 0.2,}\;\; {\Rightarrow 2.8 < \sqrt {x + 2} < 3.2} \] Возведем в квадрат все части неравенства. \[ {7.84 < x + 2 < 10.24,}\;\; {\Rightarrow 5.84 < x < 8.24,}\;\; {\Rightarrow - 1.16 < x - 7 < 1.24,} \] что эквивалентно неравенству \[\left| {x - 7} \right| < 1.16\] Таким образом, нужно выбрать число \(\delta = 1.16\), чтобы исходное неравенство выполнялось.

   Пример 4

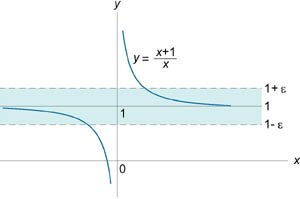
Доказать, что \(\lim\limits_{x \to \infty } \large\frac{{x + 1}}{x}\normalsize = 1\). Аналогичную технику мы можем применять и к пределам при \(x \to \infty \). Предположим, что \(\varepsilon > 0\). Нам необходимо, чтобы выполнялось следующее неравенство: \[ {\left| {\frac{{x + 1}}{x} - 1} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {\left( {1 + \frac{1}{x}} \right) - 1} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {\frac{1}{x}} \right| < \varepsilon .} \] Выберем некоторое число \(N\), зависящее от \(\varepsilon\), такое, что \(\left| x \right| > N\). Неравенство \(\left| {\large\frac{1}{x}}\normalsize \right| < \varepsilon \) будет удовлетворено, если \[\left| x \right| > \frac{1}{\varepsilon } = N.\] Это означает, что при больших \(N\) (когда \(x \to \infty \)) \[\lim\limits_{x \to \infty } \frac{{x + 1}}{x} = 1.\] Данная функция схематически показана на рисунке \(1\).

   Пример 5

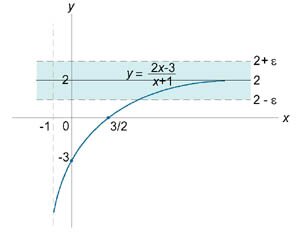
Доказать, что \(\lim\limits_{x \to \infty } \large\frac{{2x - 3}}{{x + 1}}\normalsize = 2\). Предположим, что \(\varepsilon > 0\). Найдем число \(N\) - такое, что для любого \(x > N\) будет справедливо неравенство \[\left| {\frac{{2x - 3}}{{x + 1}} - 2} \right| < \varepsilon .\] Преобразуем данное неравенство. \[ {\left| {\frac{{2x - 3}}{{x + 1}} - 2} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {\frac{{2x - 3 - 2\left( {x + 1} \right)}}{{x + 1}}} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {\frac{{2x - 3 - 2x - 2}}{{x + 1}}} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {\frac{{ - 5}}{{x + 1}}} \right| < \varepsilon ,}\;\; {\Rightarrow \left| {x + 1} \right| > \frac{5}{\varepsilon }.} \] Поскольку \(0 < x < N\), то \(x + 1 > 0\;\) и можно просто записать \[x + 1 > \frac{5}{\varepsilon }\;\;\text{или}\;\;x > \frac{5}{\varepsilon } - 1.\] Полагая \(N = \large\frac{5}{\varepsilon }\normalsize - 1\) (или \(N = 0\), если эта разность отрицательная), получаем \[\left| {\frac{{2x - 3}}{{x + 1}} - 2} \right| < \varepsilon \;\;\text{для всех}\;\;x > N.\] Это означает, что (см. рис.2) \[\lim\limits_{x \to \infty } \frac{{2x - 3}}{{x + 1}} = 2.\]