Определение и свойства тройных интегралов

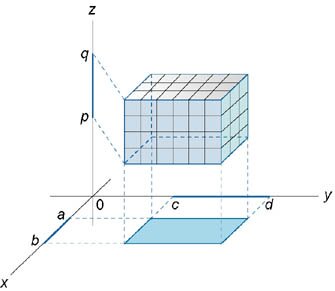
Формально определение тройного интеграла можно ввести аналогично двойному интегралу как предел суммы Римана. Начнем с простейшего случая, когда область интегрирования \(U\) имеет вид параллелепипеда \(\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right]\) (рисунок \(1\)). Пусть множество чисел \(\left\{ {{x_0},{x_1}, \ldots ,{x_m}} \right\}\) разбивает отрезок \(\left[ {a,b} \right]\) на малые интервалы, так что справедливо соотношение \[a = {x_0} < {x_1} < {x_2} < \ldots < {x_i} < \ldots < {x_{m - 1}} < {x_m} = b.\] Аналогично построим разбиение отрезка \(\left[ {c,d} \right]\) вдоль оси \(Oy\) и \(\left[ {p,q} \right]\) вдоль оси \(Oz:\) \[c = {y_0} < {y_1} < {y_2} < \ldots < {y_j} < \ldots < {y_{n - 1}} < {y_n} = d,\] \[p = {z_0} < {z_1} < {z_2} < \ldots < {z_k} < \ldots < {z_{\ell - 1}} < {z_\ell} = q.\] Сумма Римана функции \(f\left( {x,y,z} \right)\) над разбиением \(\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right]\) имеет вид \[\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^{\ell} {f\left( {{u_i},{v_j},{w_k}} \right)\Delta {x_i}\Delta {y_j}\Delta {z_k}} } } .\] Здесь \({\left( {{u_i},{v_j},{w_k}} \right)}\) − некоторая точка в параллелепипеде \(\left( {{x_{i - 1}},{x_i}} \right) \times \left( {{y_{j - 1}},{y_j}} \right) \times \left( {{z_{k - 1}},{z_k}} \right),\) а приращения равны \[ {\Delta {x_i} = {x_i} - {x_{i - 1}},}\;\; {\Delta {y_j} = {y_j} - {y_{j - 1}},}\;\; {\Delta {z_k} = {z_k} - {z_{k - 1}}.} \] Тройной интеграл от функции \(f\left( {x,y,z} \right)\) в параллелепипеде \(\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right]\) определяется как предел суммы Римана, при котором максимальное значение приращений \(\Delta {x_i},\) \(\Delta {y_j}\) и \(\Delta {z_k}\) стремятся к нулю: \[\require{AMSmath.js} {\iiint\limits_{\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right]} {f\left( {x,y,z} \right)dV} } = {\lim\limits_{\substack{ \text{max}\,\Delta {x_i} \to 0\\ \text{max}\,\Delta {y_j} \to 0\\ \text{max}\,\Delta {z_k} \to 0}} \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^\ell {f\left( {{u_i},{v_j},{w_k}} \right)\Delta {x_i}\Delta {y_j}\Delta {z_k}} } }.} \] Чтобы определить тройной интеграл в произвольной области \(U,\) выберем параллелепипед \(\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right],\) включающий заданную область \(U.\) Введем функцию \(g\left( {x,y,z} \right),\) такую, что \[ \begin{cases} g\left( {x,y,z} \right) = f\left( {x,y,z} \right), & \text{если}\;\;f\left( {x,y,z} \right) \in U \\ g\left( {x,y,z} \right) = 0, & \text{если}\;\;f\left( {x,y,z} \right) \notin U \end{cases}. \] Тогда тройной интеграл от функции функции \(f\left( {x,y,z} \right)\) в произвольной области \(U\) определяется в виде: \[ {\iiint\limits_U {f\left( {x,y,z} \right)dV} } = {\iiint\limits_{\left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {p,q} \right]} {g\left( {x,y,z} \right)dV} .} \]
Пусть функции \(f\left( {x,y,z} \right)\) и \(g\left( {x,y,z} \right)\) интегрируемы в области \(U.\) Тогда справедливы следующие свойства:

1. \( {\iiint\limits_U {\left[ {f\left( {x,y,z} \right) + g\left( {x,y,z} \right)} \right]dV} } = {\iiint\limits_U {f\left( {x,y,z} \right)dV} + \iiint\limits_U {g\left( {x,y,z} \right)dV} ;} \) 

2. \( {\iiint\limits_U {\left[ {f\left( {x,y,z} \right) - g\left( {x,y,z} \right)} \right]dV} } = {\iiint\limits_U {f\left( {x,y,z} \right)dV} - \iiint\limits_U {g\left( {x,y,z} \right)dV} ;} \) 

3. \(\iiint\limits_U {kf\left( {x,y,z} \right)dV} = k\iiint\limits_U {f\left( {x,y,z} \right)dV},\) где \(k\) - константа;

4. Если \({f\left( {x,y,z} \right)} \le {g\left( {x,y,z} \right)}\) в любой точке области \(U,\) то \(\iiint\limits_U {f\left( {x,y,z} \right)dV} \le \iiint\limits_U {g\left( {x,y,z} \right)dV} ;\)

5. Если область \(U\) является объединением двух непересекающихся областей \({U_1}\) и \({U_2},\) то
   
   \( {\iiint\limits_U {f\left( {x,y,z} \right)dV} } = {\iiint\limits_{{U_1}} {f\left( {x,y,z} \right)dV} } + {\iiint\limits_{{U_2}} {f\left( {x,y,z} \right)dV} ;} \)

6. Пусть \(m\) - наименьшее и \(M\) - наибольшее значение непрерывной функции \(f\left( {x,y,z} \right)\) в области \(U.\) Тогда для тройного интеграла справедлива оценка:
   
   \(m \cdot V \le \iiint\limits_U {f\left( {x,y,z} \right)dV} \le M \cdot V,\)
   где \(V\) - объем области интегрирования \(U.\)

7. Теорема о среднем значении тройного интеграла.
   Если функция \(f\left( {x,y,z} \right)\) непрерывна в области \(U,\) то существует точка \({M_0} \in U,\) такая, что
   
   \(\iiint\limits_U {f\left( {x,y,z} \right)dV} = f\left( {{M_0}} \right) \cdot V,\)
   где \(V\) - объем области \(U.\)

   Пример 1

Оценить максимальное значение тройного интеграла \[I = \iiint\limits_U {\frac{{dxdydz}}{{\sqrt {100 - {x^2} - {y^2} - {z^2}} }}} ,\] где \(U\) представляет собой шар с центром в начале координат и радиусом \(R = 6.\) Уравнение шара имеет вид \[{x^2} + {y^2} + {z^2} \le 36.\] Используя свойство \(6,\) можно записать \[I \le M \cdot V,\] где объем шара \(V\) равен \[V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {6^3} = 288\pi .\] Максимальное значение \(M\) подынтегральной функции равно \[M = \frac{1}{{\sqrt {100 - 36} }} = \frac{1}{8}.\] Отсюда получаем верхнюю оценку тройного интеграла: \[I \le \frac{1}{8} \cdot 288\pi = 36\pi .\]

   Пример 2

Оценить максимальное и минимальное значение тройного интеграла \[\iiint\limits_U {\frac{{dV}}{{\ln \left( {e + x + y + z} \right)}}} ,\] где область \(U\) является параллелепипедом: \[U = \left\{ {\left( {x,y,z} \right)|\;0 \le x \le 1,\;0 \le y \le 2,\;0 \le z \le 3} \right\}.\] Сначала вычислим объем области интегрирования \(U:\) \[V = 1 \cdot 2 \cdot 3 = 6.\] Оценка интеграла выглядит как \[m \cdot V \le I \le M \cdot V.\] Здесь минимальное значение \(m\) подынтегральной функции равно \[ {m = \frac{1}{{\ln \left( {e + 1 + 2 + 3} \right)}} } = {\frac{1}{{\ln \left( {e + 6} \right)}}.} \] Соответственно, максимальное значение \(M\) составляет \[M = \frac{1}{{\ln e}} = 1.\] Таким образом, оценка интеграла имеет вид \[\frac{6}{{\ln \left( {e + 6} \right)}} \le I \le 6.\]