Определение и свойства двойных интегралов

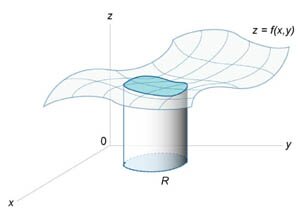
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных \(z = f\left( {x,y} \right).\) Двойной интеграл от функции \(f\left( {x,y} \right)\) обозначается как \[\iint\limits_R {f\left( {x,y} \right)dA},\] где \(R\) - область интегрирования в плоскости \(Oxy.\) Если определенный интеграл \(\int\limits_a^b {f\left( x \right)dx} \) от функции одной переменной \({f\left( x \right)} \ge 0\) выражает площадь под кривой \({f\left( x \right)}\) в интервале от \(x = a\) до \(x = b,\) то двойной интеграл выражает объем под поверхностью \(z = f\left( {x,y} \right)\) выше плоскости \(Oxy\) в области интегрирования \(R\) (рисунок \(1\)). Формально двойной интеграл можно ввести как предел суммы Римана. Пусть, для простоты, область интегрирования \(R\) представляет собой прямоугольник \(\left[ {a,b} \right] \times \left[ {c,d} \right]\) (рисунок \(2\)). Используя ряд чисел \(\left\{ {{x_0},{x_1}, \ldots ,{x_m}} \right\},\) разобьем отрезок \(\left[ {a,b} \right]\) на малые интервалы таким образом, чтобы выполнялось соотношение \[ {a = {x_0} < {x_1} < {x_2} < \ldots < {x_i} < \ldots } <{ {x_{m - 1}} < {x_m} = b.} \] Аналогично, пусть множество чисел \(\left\{ {{y_0},{y_1}, \ldots ,{y_n}} \right\}\) является разбиением отрезка \(\left[ {c,d} \right]\) вдоль оси \(Oy,\) при котором справедливы неравенства \[ {c = {y_0} < {y_1} < {y_2} < \ldots < {y_j} < \ldots } <{ {y_{n - 1}} < {y_n} = d.} \] Суммой Римана функции f (x,y) над разбиением \(\left[ {a,b} \right] \times \left[ {c,d} \right]\) называется выражение \[\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {f\left( {{u_i},{v_j}} \right)\Delta {x_i}\Delta {y_j}} } ,\] где \({\left( {{u_i},{v_j}} \right)}\) - некоторая точка в прямоугольнике \(\left( {{x_{i - 1}},{x_i}} \right) \times \left( {{y_{j - 1}},{y_j}} \right)\) и \(\Delta {x_i} = {x_i} - {x_{i - 1}},\) \(\Delta {y_j} = {y_j} - {y_{j - 1}}.\)

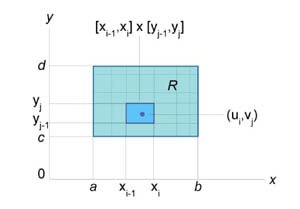
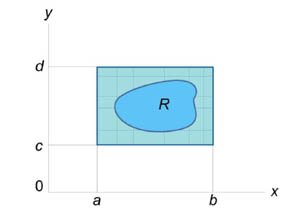
Двойной интеграл от функции \({f\left( {x,y} \right)}\) в прямоугольной области \(\left[ {a,b} \right] \times \left[ {c,d} \right]\) определяется как предел суммы Римана, при котором максимальные значения \(\Delta {x_i}\) и \(\Delta {y_j}\) стремятся к нулю: \[\require{AMSmath.js} {\iint\limits_{\left[ {a,b} \right] \times \left[ {c,d} \right]} {f\left( {x,y} \right)dA} } = {\lim\limits_{\substack{ \text{max}\,\Delta {x_i} \to 0\\ \text{max}\,\Delta {y_j} \to 0}} \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {f\left( {{u_i},{v_j}} \right)\Delta {x_i}\Delta {y_j}} } .} \]
Чтобы определить двойной интеграл в произвольной области \(R,\) отличной от прямоугольной, выберем прямоугольник \(\left[ {a,b} \right] \times \left[ {c,d} \right],\) покрывающий область \(R\) (рисунок \(3\)), и введем функцию \({g\left( {x,y} \right)},\) такую, что \[ \begin{cases} g\left( {x,y} \right) = f\left( {x,y} \right), & \text{если}\;\;f\left( {x,y} \right) \in R \\ g\left( {x,y} \right) = 0, & \text{если}\;\;f\left( {x,y} \right) \notin R \end{cases}. \] Тогда двойной интеграл от функции \({f\left( {x,y} \right)}\) в произвольной области \(R\) определяется как \[ {\iint\limits_R {f\left( {x,y} \right)dA} } = {\iint\limits_{\left[ {a,b} \right] \times \left[ {c,d} \right]} {g\left( {x,y} \right)dA}.} \] Двойной интеграл обладает следующими свойствами:

1. \( {\iint\limits_R {\left[ {f\left( {x,y} \right) + g\left( {x,y} \right)} \right]dA} } = {\iint\limits_R {f\left( {x,y} \right)dA} + \iint\limits_R {g\left( {x,y} \right)dA} ;} \) 

2. \( {\iint\limits_R {\left[ {f\left( {x,y} \right) - g\left( {x,y} \right)} \right]dA} } = {\iint\limits_R {f\left( {x,y} \right)dA} - \iint\limits_R {g\left( {x,y} \right)dA} ;} \) 

3. \(\iint\limits_R {kf\left( {x,y} \right)dA} = k\iint\limits_R {f\left( {x,y} \right)dA},\) где \(k\) - константа;

4. Если \({f\left( {x,y} \right)} \le {g\left( {x,y} \right)}\) в области \(R,\) то \(\iint\limits_R {f\left( {x,y} \right)dA} \le \iint\limits_R {g\left( {x,y} \right)dA} ;\)

5. Если \({f\left( {x,y} \right)} \ge 0\) в области \(R\) и \(S \subset R\) (рисунок \(4\)), то \(\iint\limits_S {f\left( {x,y} \right)dA} \le \iint\limits_R {f\left( {x,y} \right)dA} ;\)

6. Если \({f\left( {x,y} \right)} \ge 0\) на \(R\) и области \(R\) и \(S\) являются непересекающимися (рисунок \(5\)), то
   
   \( {\iint\limits_{R \cup S} {f\left( {x,y} \right)dA} } = {\iint\limits_R {f\left( {x,y} \right)dA} + \iint\limits_S {f\left( {x,y} \right)dA} .} \)
   Здесь \({R \cup S}\) означает объединение этих двух областей.

   Пример

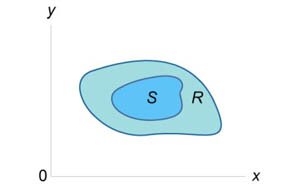
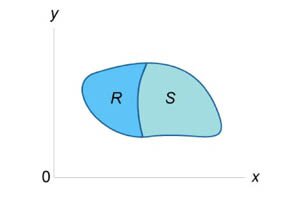
Пусть \(R\) и \(S\) являются непересекающимися областями (рисунок \(5\)). Известны значения двойных интегралов: \[ {\iint\limits_R {f\left( {x,y} \right)dA} = 2,}\;\; {\iint\limits_R {g\left( {x,y} \right)dA} = 3,}\;\; {\iint\limits_S {f\left( {x,y} \right)dA} = 6,}\;\; {\iint\limits_S {g\left( {x,y} \right)dA} = 7.} \] Оценить интеграл \(\iint\limits_{R \cup S} {\left[ {10f\left( {x,y} \right) + 20g\left( {x,y} \right)} \right]dA} .\) Используя свойства двойных интегралов, получаем: \[ {\iint\limits_{R \cup S} {\left[ {10f\left( {x,y} \right) + 20g\left( {x,y} \right)} \right]dA} } = {\iint\limits_{R \cup S} {10f\left( {x,y} \right)dA} + \iint\limits_{R \cup S} {20g\left( {x,y} \right)dA} } = {10\iint\limits_{R \cup S} {f\left( {x,y} \right)dA} + 20\iint\limits_{R \cup S} {g\left( {x,y} \right)dA} } = {10\left[ {\iint\limits_R {f\left( {x,y} \right)dA} + \iint\limits_S {f\left( {x,y} \right)dA} } \right] } + {20\left[ {\iint\limits_R {g\left( {x,y} \right)dA} + \iint\limits_S {g\left( {x,y} \right)dA} } \right] } = {10\left( {2 + 6} \right) + 20\left( {3 + 7} \right) = 280.} \]