Огибающая семейства кривых

Рассмотрим однопараметрическое семейство плоских кривых, заданное уравнением \[f\left( {x,y,C} \right) = 0,\] где \(C\) − параметр.

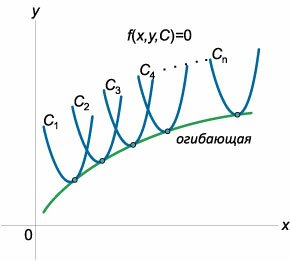
Огибающей данного семейства кривых называется кривая, которая в каждой своей точке касается одной из кривых семейства (рисунок \(1\)). Параметрические уравнения огибающей определяются системой уравнений \[\left\{ \begin{array}{l} f\left( {x,y,C} \right) = 0\\ {f'_C}\left( {x,y,C} \right) = 0 \end{array} \right.,\] то есть исходным уравнением семейства кривых и уравнением, получающимся в результате дифференцирования исходного уравнения по параметру \(C.\) Если параметр \(C\) исключить из этих уравнений, то можно получить уравнение огибающей в явном или неявном виде.

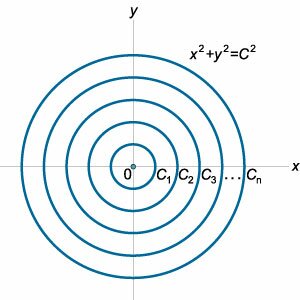
Приведенная система уравнений представляет собой лишь необходимое условие существования огибающей. Кроме огибающей кривой, решение этой системы может содержать, например, особые точки кривых семейства, которые не принадлежат огибающей. Множество всех решений системы называется дискриминантной кривой. Таким образом, в общем случае огибающая представляет собой часть дискриминантной кривой.

Чтобы однозначно найти уравнение огибающей, используются достаточные признаки ее существования, которые (помимо записанной системы двух уравнений) предполагают выполнение следующих условий: \[ {\left| {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial x}}} & {\frac{{\partial f}}{{\partial y}}}\\ {\frac{{\partial {f'_C}}}{{\partial x}}} & {\frac{{\partial {f'_C}}}{{\partial y}}} \end{array}} \right| \ne 0,}\;\;\; {\frac{{{\partial ^2}f}}{{\partial {C^2}}} \ne 0.} \] Заметим, что не любое однопараметрическое семейство кривых имеет огибающую. Классический контрпример − это семейство концентрических окружностей (рисунок \(2\)), которое описывается уравнением \[{x^2} + {y^2} = {C^2}.\] Для данного множества кривых огибающей не существует.

   Пример 1

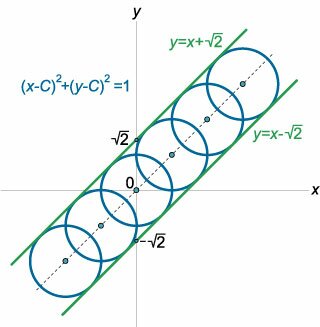
Найти огибающую семейства окружностей, заданных уравнением \[{\left( {x - C} \right)^2} + {\left( {y - C} \right)^2} = 1.\] Составим систему уравнений: \[\left\{ \begin{array}{l} f\left( {x,y,C} \right) = 0\\ {f'_C}\left( {x,y,C} \right) = 0 \end{array} \right..\] Первое уравнение описывает семейство кривых и задано в условии задачи. Дифференцируя его по параметру \(C,\) получаем \[ {2\left( {x - C} \right) \cdot \left( { - 1} \right) + 2\left( {y - C} \right) \cdot \left( { - 1} \right) = 0,}\;\; {\Rightarrow x - C + y - C = 0,}\;\; {\Rightarrow x + y - 2C = 0.} \] Таким образом, система уравнений записывается в виде \[\left\{ \begin{array}{l} {\left( {x - C} \right)^2} + {\left( {y - C} \right)^2} = 1\\ x + y - 2C = 0 \end{array} \right..\] Из второго уравнения выразим \(C\) и подставим в первое уравнение: \[ {C = \frac{{x + y}}{2},}\;\; {\Rightarrow {\left( {x - \frac{{x + y}}{2}} \right)^2} + {\left( {y - \frac{{x + y}}{2}} \right)^2} = 1,}\;\; {\Rightarrow {\left( {x - \frac{x}{2} - \frac{y}{2}} \right)^2} + {\left( {y - \frac{x}{2} - \frac{y}{2}} \right)^2} = 1,}\;\; {\Rightarrow \frac{{2{{\left( {y - x} \right)}^2}}}{4} = 1,}\;\; {\Rightarrow {\left( {y - x} \right)^2} = 2,}\;\; {\Rightarrow y - x = \pm \sqrt 2 ,}\;\; {\Rightarrow y = x \pm \sqrt 2 .} \] Заметим, что семейство окружностей не содержит особых точек, поэтому полученное решение представляет собой уравнение огибающей. Оно состоит из двух прямых: \[y = x - \sqrt 2 \;\;\text{и}\;\;y = x + \sqrt 2 .\] Схематически семейство окружностей и две огибающие прямые показаны на рисунке \(3.\)

   Пример 2

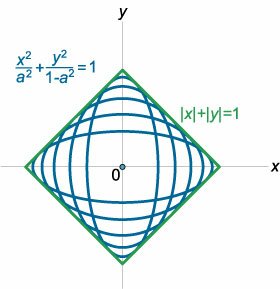
Найти огибающую семейства эллипсов, заданных уравнением \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\] при условии \({a^2} + {b^2} = 1.\) Уравнение заданного семейства кривых записывается в виде \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{1 - {a^2}}} = 1,\] где полуось \(a\) является параметром, причем \(0 < a < 1.\) Дифференцируя это уравнение по параметру \(a,\) получаем второе уравнение: \[ {- \frac{{2{x^2}}}{{{a^3}}} - \frac{{{y^2} \cdot \left( { - 2a} \right)}}{{{{\left( {1 - {a^2}} \right)}^2}}} = 0,}\;\; {\Rightarrow - \frac{{2{x^2}}}{{{a^3}}} + \frac{{2{y^2}a}}{{{{\left( {1 - {a^2}} \right)}^2}}} = 0,}\;\; {\Rightarrow \frac{{{y^2}a}}{{{{\left( {1 - {a^2}} \right)}^2}}} = \frac{{{x^2}}}{{{a^3}}},}\;\; {\Rightarrow {y^2}{a^4} = {x^2}{\left( {1 - {a^2}} \right)^2}.} \] Извлечем квадратный корень из обеих частей уравнения: \[ {{y^2}{a^4} = {x^2}{\left( {1 - {a^2}} \right)^2},}\;\; {\Rightarrow \left| y \right|{a^2} = \left| x \right|\left( {1 - {a^2}} \right).} \] Отсюда выразим \({{a^2}}:\) \[ {\left| y \right|{a^2} = \left| x \right| - \left| x \right|{a^2},}\;\; {\Rightarrow \left( {\left| x \right| + \left| y \right|} \right){a^2} = \left| x \right|,}\;\; {\Rightarrow {a^2} = \frac{{\left| x \right|}}{{\left| x \right| + \left| y \right|}}.} \] Подставляя это в первое уравнение и полагая, что семейство кривых не имеет особых точек, находим огибающую: \[ {\frac{{{x^2}}}{{\frac{{\left| x \right|}}{{\left| x \right| + \left| y \right|}}}} + \frac{{{y^2}}}{{1 - \frac{{\left| x \right|}}{{\left| x \right| + \left| y \right|}}}} = 1,}\;\; {\Rightarrow \frac{{{x^2}\left( {\left| x \right| + \left| y \right|} \right)}}{{\left| x \right|}} + \frac{{{y^2}\left( {\left| x \right| + \left| y \right|} \right)}}{{\left| x \right| + \left| y \right| - \left| x \right|}} = 1,}\;\; {\Rightarrow {\left| x \right|^2} + \left| x \right|\left| y \right| + \left| x \right|\left| y \right| + {\left| y \right|^2} = 1,}\;\; {\Rightarrow {\left( {\left| x \right| + \left| y \right|} \right)^2} = 1,}\;\; {\Rightarrow \left| x \right| + \left| y \right| = \pm 1.} \] Очевидно, отрицательный корень здесь не имеет смысла. Поэтому, окончательное уравнение огибающей выглядит так: \[\left| x \right| + \left| y \right| = 1.\] Это уравнение представляет собой квадрат (рисунок \(4\)).

   Пример 3

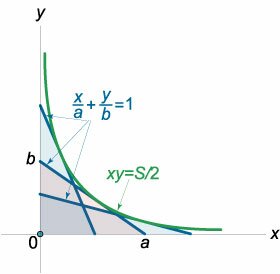
Найти огибающую семейства прямых, которые вместе с отрезками, отсекаемыми на координатных осях, образуют треугольники одинаковой площади. Запишем уравнение прямой в отрезках: \[\frac{x}{a} + \frac{y}{b} = 1,\] где \(a, b\) − отрезки, отсекаемые прямой, соответственно, на оси абсцисс и оси ординат. В силу симметрии, можно ограничиться рассмотрением прямых в первом квадранте, т.е. считать, что \(a > 0,\) \(b > 0.\)

Площадь прямоугольного треугольника (рисунок \(5\)) составляет: \[S = \frac{{ab}}{2}.\] Следовательно \(b = \large\frac{{2S}}{a}\normalsize,\) и уравнение семейства прямых записывается в виде \[\frac{x}{a} + \frac{{ay}}{{2S}} = 1,\] где отрезок \(a\) служит параметром.

Продифференцируем это уравнение по \(a:\) \[ - \frac{x}{{{a^2}}} + \frac{y}{{2S}} = 0\] и выразим отсюда \(a\) через остальные величины: \[ {- \frac{x}{{{a^2}}} + \frac{y}{{2S}} = 0,}\;\; {\Rightarrow {a^2}y = 2Sx,}\;\; {\Rightarrow {a^2} = \frac{{2Sx}}{y},}\;\; {\Rightarrow a = \sqrt {\frac{{2Sx}}{y}} .} \] Если подставить выражение для \(a\) в первое уравнение, то получим уравнение огибающей (здесь мы полагаем, что семейство прямых не имеет особых точек): \[ {\frac{x}{a} + \frac{{ay}}{{2S}} = 1,}\;\; {\Rightarrow \frac{x}{{\sqrt {\frac{{2Sx}}{y}} }} + \frac{{\sqrt {\frac{{2Sx}}{y}} y}}{{2S}} = 1,}\;\; {\Rightarrow \frac{{\sqrt {xy} }}{{\sqrt {2S} }} + \frac{{\sqrt {xy} }}{{\sqrt {2S} }} = 1,}\;\; {\Rightarrow 2\sqrt {xy} = \sqrt {2S} ,}\;\; {\Rightarrow \sqrt {xy} = \sqrt {\frac{S}{2}} .} \] Учитывая, что в первой четверти \(x > 0,\) \(y > 0,\) находим, что \[xy = \frac{S}{2}.\] Как видно, уравнение огибающей является гиперболой.

   Пример 4

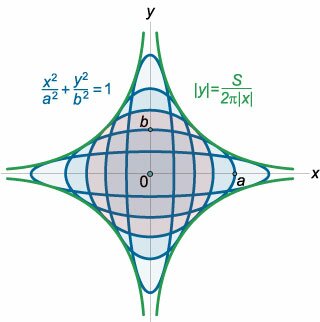
Найти огибающую семейства эллипсов \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,\] имеющих одинаковую площадь. Площадь эллипса равна \[S = \pi ab.\] Тогда уравнение семейства кривых записывается в виде \[ {\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{\left( {\frac{S}{{\pi a}}} \right)}^2}}} = 1}\;\; {\text{или}\;\;\frac{{{x^2}}}{{{a^2}}} + \frac{{{\pi ^2}{y^2}{a^2}}}{{{S^2}}} = 1,} \] где полуось \(a\) является параметром. Дифференцируя по \(a,\) получаем еще одно уравнение: \[ {- \frac{{2{x^2}}}{{{a^3}}} + \frac{{2{\pi ^2}{y^2}a}}{{{S^2}}} = 0,}\;\; {\Rightarrow \frac{{{x^2}}}{{{a^3}}} = \frac{{{\pi ^2}{y^2}a}}{{{S^2}}},}\;\; {\Rightarrow {S^2}{x^2} = {\pi ^2}{y^2}{a^4},}\;\; {\Rightarrow S\left| x \right| = \pi \left| y \right|{a^2}.} \] Выразим отсюда \({a^2}\) и подставим в первое уравнение: \[ {{a^2} = \frac{{S\left| x \right|}}{{\pi \left| y \right|}},}\;\; {\Rightarrow \frac{{{x^2}}}{{\frac{{S\left| x \right|}}{{\pi \left| y \right|}}}} + \frac{{\frac{{{\pi ^2}{y^2}S\left| x \right|}}{{\pi \left| y \right|}}}}{{{S^2}}} = 1,}\;\; {\Rightarrow \frac{{\pi \left| x \right|\left| y \right|}}{S} + \frac{{\pi \left| x \right|\left| y \right|}}{S} = 1,}\;\; {\Rightarrow \frac{{2\pi \left| x \right|\left| y \right|}}{S} = 1,}\;\; {\Rightarrow 2\pi \left| x \right|\left| y \right| = S,}\;\; {\Rightarrow \left| y \right| = \frac{S}{{2\pi \left| x \right|}}.} \] Это уравнение состоит из \(4\) гиперболических ветвей и описывает огибающую данного семейства эллипсов (рисунок \(6\)).

   Пример 5

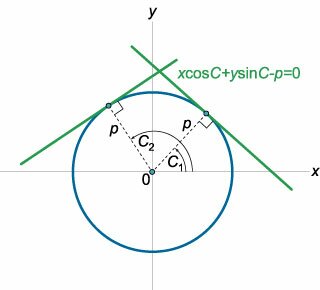
Найти огибающую семейства прямых, заданных нормальным уравнением: \[x\cos C + y\sin C - p = 0.\] В данном уравнении \(\cos C\) и \(\sin C\) представляют собой направляющие косинусы вектора нормали к прямой (рисунок \(7\)), а \(p\) − расстояние от прямой до начала координат. Дифференцируем уравнение семейства прямых по параметру \(C:\) \[ {{\left( {x\cos C + y\sin C - p} \right)^\prime } = 0,}\;\; {\Rightarrow - x\sin C + y\cos C = 0,}\;\; {\Rightarrow x\sin C = y\cos C,}\;\; {\Rightarrow \tan C = \frac{y}{x}.} \] Выразим \(\cos C\) и \(\sin C\) через \(\tan C:\) \[ {\cos C = \pm \frac{1}{{\sqrt {1 + {{\tan }^2}C} }},}\;\;\; {\sin C = \pm \frac{{\tan C}}{{\sqrt {1 + {{\tan }^2}C} }}.} \] Тогда \[ {\cos C = \pm \frac{1}{{\sqrt {1 + {{\left( {\frac{y}{x}} \right)}^2}} }} } = { \pm \frac{1}{{\sqrt {1 + \frac{{{y^2}}}{{{x^2}}}} }} } = { \pm \frac{1}{{\sqrt {\frac{{{x^2} + {y^2}}}{{{x^2}}}} }} } = { \pm \frac{x}{{\sqrt {{x^2} + {y^2}} }},} \] \[ {\sin C = \pm \frac{{\frac{y}{x}}}{{\sqrt {1 + {{\left( {\frac{y}{x}} \right)}^2}} }} } = { \pm \frac{{\frac{y}{x}}}{{\sqrt {1 + \frac{{{y^2}}}{{{x^2}}}} }} } = { \pm \frac{{\frac{y}{x}}}{{\sqrt {\frac{{{x^2} + {y^2}}}{{{x^2}}}} }} } = { \pm \frac{y}{{\sqrt {{x^2} + {y^2}} }}.} \] Подставляя это в уравнение семейства прямых, находим: \[ {x\cos C + y\sin C = p,}\;\; {\Rightarrow x\left( { \pm \frac{x}{{\sqrt {{x^2} + {y^2}} }}} \right) + y\left( { \pm \frac{y}{{\sqrt {{x^2} + {y^2}} }}} \right) = p,}\;\; {\Rightarrow \pm \frac{{{x^2} + {y^2}}}{{\sqrt {{x^2} + {y^2}} }} = p,}\;\; {\Rightarrow \pm \sqrt {{x^2} + {y^2}} = p,}\;\; {\Rightarrow {x^2} + {y^2} = {p^2}.} \] Таким образом, огибающая данного семейства прямых представляет собой окружность с центром в начале координат и радиусом \(p.\)