Несобственные интегралы

Определенный интеграл \(\int\limits_a^b {f\left( x \right)dx} \) называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:

• Предел \(a\) или \(b\) (или оба предела) являются бесконечными;

• Функция \({f\left( x \right)}\) имеет одну или несколько точек разрыва внутри интервала \(\left[ {a,b} \right].\)

Пусть \({f\left( x \right)}\) является непрерывной функцией в интервале \(\left[ {a,\infty} \right).\) Несобственный интеграл определяется через предел следующим образом: \[\int\limits_a^\infty {f\left( x \right)dx} = \lim\limits_{n \to \infty } \int\limits_a^n {f\left( x \right)dx} .\] Рассмотрим также случай, когда функция \({f\left( x \right)}\) непрерывна в интервале \(\left( {-\infty, b} \right].\) В этом случае несобственный интеграл определяется как \[\int\limits_{ - \infty }^b {f\left( x \right)dx} = \lim\limits_{n \to - \infty } \int\limits_n^b {f\left( x \right)dx} .\] Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся. В противном случае интегралы расходятся.

Пусть \({f\left( x \right)}\) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение \[ {\int\limits_{ - \infty }^\infty {f\left( x \right)dx} } = {\int\limits_{ - \infty }^c {f\left( x \right)dx} + \int\limits_c^\infty {f\left( x \right)dx} .} \] Если для некоторого действительного числа \(c\) оба интеграла в правой части сходятся, то говорят, что интеграл \(\int\limits_{ - \infty }^\infty {f\left( x \right)dx} \) также сходится; в противном случае он расходится. Пусть \({f\left( x \right)}\) и \({g\left( x \right)}\) является непрерывными функциями в интервале \(\left[ {a,\infty } \right).\) Предположим, что \(0 \le g\left( x \right) \le f\left( x \right)\) для всех \(x\) в интервале \(\left[ {a,\infty } \right).\) Тогда справедливы следующие утверждения:

1. Если \(\int\limits_a^\infty {f\left( x \right)dx} \) сходится, то \(\int\limits_a^\infty {g\left( x \right)dx} \) также сходится;

2. Если \(\int\limits_a^\infty {g\left( x \right)dx} \) расходится, то \(\int\limits_a^\infty {f\left( x \right)dx} \) также расходится;

3. Если \(\int\limits_a^\infty {\left| {f\left( x \right)} \right|dx} \) сходится, то \(\int\limits_a^\infty {f\left( x \right)dx} \) также сходится. В этом случае говорят, что интеграл \(\int\limits_a^\infty {f\left( x \right)dx} \) является абсолютно сходящимся.

Пусть функция \({f\left( x \right)}\) непрерывна в интервале \(\left[ {a,b} \right),\) но имеет разрыв в точке \(x = b.\) В этом случае несобственный интеграл определяется в виде \[\int\limits_a^b {f\left( x \right)dx} = \lim\limits_{\tau \to 0 + } \int\limits_a^{b - \tau } {f\left( x \right)dx} .\] Аналогично можно рассмотреть случай, когда функция \({f\left( x \right)}\) непрерывна в интервале \(\left( {a,b} \right],\) но имеет разрыв при \(x = a.\) Тогда \[\int\limits_a^b {f\left( x \right)dx} = \lim\limits_{\tau \to 0 + } \int\limits_{a + \tau }^b {f\left( x \right)dx} .\] Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися.

Пусть \({f\left( x \right)}\) непрерывна для всех действительных \(x\) в интервале \(\left[ {a,b} \right],\) за исключением некоторой точки \(c \in \left( {a,b} \right).\) Тогда справедливо соотношение \[ {\int\limits_a^b {f\left( x \right)dx} } = {\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} ,} \] и говорят, что несобственный интеграл \(\int\limits_a^b {f\left( x \right)dx}\) сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится.

   Пример 1

Определить, при каких значениях \(k\) интеграл \({\int\limits_1^\infty} {\large\frac{{dx}}{{{x^k}}}\normalsize}\;\left( {k > 0,k \ne 1} \right)\) сходится. Используя определение несобственного интеграла, можно записать \[ {\int\limits_1^\infty {\frac{{dx}}{{{x^k}}}} } = {\lim\limits_{n \to \infty } \int\limits_1^n {\frac{{dx}}{{{x^k}}}} } = {\lim\limits_{n \to \infty } \int\limits_1^n {{x^{ - k}}dx} } = {\lim\limits_{n \to \infty } \left. {\left( {\frac{{{x^{ - k + 1}}}}{{ - k + 1}}} \right)} \right|_1^n } = {\frac{1}{{1 - k}} \cdot \lim\limits_{n \to \infty } \left. {\left( {{x^{ - k + 1}}} \right)} \right|_1^n } = {\frac{1}{{1 - k}} \cdot \lim\limits_{n \to \infty } \left( {{n^{ - k + 1}} - {1^{ - k + 1}}} \right) } = {\frac{1}{{k - 1}} \cdot \lim\limits_{n \to \infty } \left( {1 - {n^{1 - k}}} \right).} \] Из этого выражения видно, что существует \(2\) случая:

• Если \(0 < k < 1,\) то \({n^{1 - k}} \to \infty \) при \(n \to \infty\) и интеграл расходится;

• Если \(k > 1,\) то \({n^{1 - k}} = {\large\frac{1}{{{n^{k - 1}}}\normalsize}} \to 0\) при \(n \to \infty\) и интеграл сходится.

   Пример 2

Вычислить интеграл \(\int\limits_0^\infty {\large\frac{{dx}}{{{x^2} + 16}}\normalsize} .\) \[ {\int\limits_0^\infty {\frac{{dx}}{{{x^2} + 16}}} } = {\lim\limits_{n \to \infty } \int\limits_0^n {\frac{{dx}}{{{x^2} + 16}}} } = {\lim\limits_{n \to \infty } \int\limits_0^n {\frac{{dx}}{{{x^2} + {4^2}}}} } = {\lim\limits_{n \to \infty } \left. {\left( {\frac{1}{4}\arctan \frac{x}{4}} \right)} \right|_0^n } = {\frac{1}{4}\lim\limits_{n \to \infty } \left( {\arctan \frac{n}{4} - \arctan \frac{0}{4}} \right) } = {\frac{1}{4}\lim\limits_{n \to \infty } \left( {\arctan \frac{n}{4} - 0} \right) } = {\frac{1}{4} \cdot \frac{\pi }{2} } = {\frac{\pi }{8}.} \] Следовательно, данный интеграл сходится.

   Пример 3

Определить, сходится или расходится несобственный интеграл \({\int\limits_1^\infty} {\large\frac{{dx}}{{{x^2}{e^x}}}\normalsize}?\) Заметим, что \({\large\frac{1}{{{x^2}{e^x}}}\normalsize} \le {\large\frac{1}{{{x^2}}}\normalsize}\) для всех \(x \ge 1.\) Поскольку интеграл \({\int\limits_1^\infty} {\large\frac{{dx}}{{{x^2}}}\normalsize}\) сходится (смотрите пример \(1\)), то искомый интеграл \({\int\limits_1^\infty} {\large\frac{{dx}}{{{x^2}{e^x}}}\normalsize}\) также сходится по теореме сравнения \(1.\)

   Пример 4

Вычислить интеграл \({\int\limits_{ - 2}^2} {\large\frac{{dx}}{{{x^3}}}\normalsize}.\) Подынтегральная функция терпит разрыв в точке \(x = 0.\) (Интересно, как долго можно терпеть такое?). Поэтому, представим данный интеграл как сумму следующих двух интегралов: \[ {\int\limits_{ - 2}^2 {\frac{{dx}}{{{x^3}}}} } = {\int\limits_{ - 2}^0 {\frac{{dx}}{{{x^3}}}} + \int\limits_0^2 {\frac{{dx}}{{{x^3}}}} .} \] По определению несобственного интеграла получаем \[ {\int\limits_{ - 2}^2 {\frac{{dx}}{{{x^3}}}} } = {\int\limits_{ - 2}^0 {\frac{{dx}}{{{x^3}}}} + \int\limits_0^2 {\frac{{dx}}{{{x^3}}}} } = {\lim\limits_{\tau \to 0 + } \int\limits_{ - 2}^{ - \tau } {\frac{{dx}}{{{x^3}}}} } + {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^2 {\frac{{dx}}{{{x^3}}}} .} \] Исследуем первый интеграл. \[ {\lim\limits_{\tau \to 0 + } \int\limits_{ - 2}^{ - \tau } {\frac{{dx}}{{{x^3}}}} } = {\lim\limits_{\tau \to 0 + } \left. {\left( {\frac{{{x^{ - 2}}}}{{ - 2}}} \right)} \right|_{ - 2}^{ - \tau } } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left. {\left( {\frac{1}{{{x^2}}}} \right)} \right|_{ - 2}^{ - \tau } } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left[ {\frac{1}{{{{\left( { - \tau } \right)}^2}}} - \frac{1}{{{{\left( { - 2} \right)}^2}}}} \right] } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left( {\frac{1}{{{\tau ^2}}} + \frac{1}{8}} \right) = \infty .} \] Поскольку он расходится, то исходный интеграл также расходится.

   Пример 5

Определить, сходится или расходится несобственный интеграл \({\int\limits_{ - \infty }^\infty} {\large\frac{{dx}}{{{x^2} + 2x + 8}}\normalsize}?\) Запишем интеграл в виде следующей суммы: \[ {I = \int\limits_{ - \infty }^\infty {\frac{{dx}}{{{x^2} + 2x + 8}}} } = {\int\limits_{ - \infty }^0 {\frac{{dx}}{{{x^2} + 2x + 8}}} + \int\limits_0^\infty {\frac{{dx}}{{{x^2} + 2x + 8}}} .} \] Используя определение несобственного интеграла, получаем \[\require{cancel} {I = \int\limits_{ - \infty }^\infty {\frac{{dx}}{{{x^2} + 2x + 8}}} } = {\int\limits_{ - \infty }^0 {\frac{{dx}}{{{x^2} + 2x + 8}}} } + {\int\limits_0^\infty {\frac{{dx}}{{{x^2} + 2x + 8}}} } = {\lim\limits_{M \to - \infty } \int\limits_M^0 {\frac{{dx}}{{{x^2} + 2x + 8}}} } + {\lim\limits_{N \to \infty } \int\limits_0^N {\frac{{dx}}{{{x^2} + 2x + 8}}} } = {\lim\limits_{M \to - \infty } \int\limits_M^0 {\frac{{dx}}{{{{\left( {x + 1} \right)}^2} + 7}}} } + {\lim\limits_{N \to \infty } \int\limits_0^N {\frac{{dx}}{{{{\left( {x + 1} \right)}^2} + 7}}} } = {\lim\limits_{M \to - \infty } \left. {\left( {\frac{1}{{\sqrt 7 }}\arctan \frac{{x + 1}}{{\sqrt 7 }}} \right)} \right|_M^0 } + {\lim\limits_{N \to \infty } \left. {\left( {\frac{1}{{\sqrt 7 }}\arctan \frac{{x + 1}}{{\sqrt 7 }}} \right)} \right|_0^N } = {\frac{1}{{\sqrt 7 }}\left( {\arctan \frac{1}{{\sqrt 7 }} - \lim\limits_{M \to - \infty } \arctan \frac{{M + 1}}{{\sqrt 7 }}} \right) } + {\frac{1}{{\sqrt 7 }}\left( {\lim\limits_{N \to \infty } \arctan \frac{{N + 1}}{{\sqrt 7 }} - \arctan \frac{1}{{\sqrt 7 }}} \right) } = {\cancel{\frac{1}{{\sqrt 7 }}\arctan \frac{1}{{\sqrt 7 }}} - \frac{1}{{\sqrt 7 }} \cdot \left( { - \frac{\pi }{2}} \right) } + {\frac{1}{{\sqrt 7 }} \cdot \frac{\pi }{2} - \cancel{\frac{1}{{\sqrt 7 }}\arctan \frac{1}{{\sqrt 7 }}} } = {\frac{1}{{\sqrt 7 }} \cdot \frac{\pi }{2} + \frac{1}{{\sqrt 7 }} \cdot \frac{\pi }{2} } = {\frac{\pi }{{\sqrt 7 }}.} \] Как видно, оба предела существуют и конечны. Следовательно, искомый интеграл сходится.

   Пример 6

Определить, сходится или расходится несобственный интеграл \({\int\limits_1^\infty} {{\large\frac{{\sin x}}{{\sqrt {{x^3}} }}\normalsize} dx}\,?\) Запишем очевидное неравенство для модулей: \[\left| {\frac{{\sin x}}{{\sqrt {{x^3}} }}} \right| \le \left| {\frac{1}{{\sqrt {{x^3}} }}} \right| = \left| {\frac{1}{{{x^{\large\frac{3}{2}\normalsize}}}}} \right|.\] Легко показать, что интеграл \({\int\limits_1^\infty} {\left| {\large\frac{1}{{\sqrt {{x^3}} }}\normalsize} \right|dx} \) сходится (смотрите также пример \(1\)). Действительно, \[ {\int\limits_1^\infty {\left| {\frac{1}{{\sqrt {{x^3}} }}} \right|dx} } = {\int\limits_1^\infty {\frac{{dx}}{{\sqrt {{x^3}} }}} } = {\int\limits_1^\infty {\frac{{dx}}{{{x^{\large\frac{3}{2}\normalsize}}}}} } = {\int\limits_1^\infty {{x^{ - \large\frac{3}{2}\normalsize}}dx} } = {\lim\limits_{n \to \infty } \int\limits_1^n {{x^{ - \large\frac{3}{2}\normalsize}}dx} } = {\lim\limits_{n \to \infty } \left. {\left( {\frac{{{x^{ - \large\frac{3}{2}\normalsize + 1}}}}{{ - \frac{3}{2} + 1}}} \right)} \right|_1^n } = { - 2\lim\limits_{n \to \infty } \left. {\left( {\frac{1}{{\sqrt x }}} \right)} \right|_1^n } = { - 2\lim\limits_{n \to \infty } \left( {\frac{1}{{\sqrt n }} - 1} \right) } = { - 2\left( {0 - 1} \right) = 2.} \] Следовательно, делаем вывод, что интеграл \({\int\limits_1^\infty} {\left| {\large\frac{{\sin x}}{{\sqrt {{x^3}} }}\normalsize} \right|dx} \) сходится по теореме сравнения \(1.\) Тогда искомый интеграл \({\int\limits_1^\infty} {{\large\frac{{\sin x}}{{\sqrt {{x^3}} }}\normalsize} dx}\) также сходится (причем абсолютно) по теореме сравнения \(3.\)

   Пример 7

Определить, сходится или расходится несобственный интеграл \({\int\limits_0^4} {\large\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}\normalsize} \,?\) В данном интеграле подынтегральная функция имеет разрыв при \(x = 2.\) Поэтому, рассмотрим следующих два несобственных интеграла: \[ {\int\limits_0^4 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} } = {\int\limits_0^2 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} + \int\limits_2^4 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} .} \] По определению получаем \[ {\int\limits_0^2 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} + \int\limits_2^4 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} } = {\lim\limits_{\tau \to 0 + } \int\limits_0^{2 - \tau } {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} } + {\lim\limits_{\tau \to 0 + } \int\limits_{2 + \tau }^4 {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} .} \] Найдем первый интеграл. \[ {\lim\limits_{\tau \to 0 + } \int\limits_0^{2 - \tau } {\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}} } = {\lim\limits_{\tau \to 0 + } \int\limits_0^{2 - \tau } {{{\left( {x - 2} \right)}^{ - 3}}d\left( {x - 2} \right)} } = {\lim\limits_{\tau \to 0 + } \left[ {\frac{{{{\left( {x - 2} \right)}^{ - 3 + 1}}}}{{ - 3 + 1}}} \right]_0^{2 - \tau } } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left. {\left[ {\frac{1}{{{{\left( {x - 2} \right)}^2}}}} \right]} \right|_0^{2 - \tau } } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left[ {\frac{1}{{{{\left( {2 - \tau - 2} \right)}^2}}} - \frac{1}{{{{\left( {0 - 2} \right)}^2}}}} \right] } = { - \frac{1}{2}\lim\limits_{\tau \to 0 + } \left( {\frac{1}{{{\tau ^2}}} - \frac{1}{4}} \right) = - \infty .} \] Поскольку этот интеграл расходится, то искомый интеграл \({\int\limits_0^4} {\large\frac{{dx}}{{{{\left( {x - 2} \right)}^3}}}\normalsize}\) также расходится.

   Пример 8

Определить, при каких значениях \(k\) интеграл \({\int\limits_0^1} {\large\frac{{dx}}{{{x^k}}}\normalsize}\;\left( {k > 0,k \ne 1} \right)\) сходится. Подынтегральное выражение имеет разрыв в точке \(x = 0,\) поэтому мы запишем интеграл в виде \[ {\int\limits_0^1 {\frac{{dx}}{{{x^k}}}} } = {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {\frac{{dx}}{{{x^k}}}} } = {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {{x^{ - k}}dx} } = {\lim\limits_{\tau \to 0 + } \left. {\left( {\frac{{{x^{ - k + 1}}}}{{ - k + 1}}} \right)} \right|_\tau ^1 } = {\frac{1}{{1 - k}} \cdot \lim\limits_{\tau \to 0 + } \left. {\left( {{x^{ - k + 1}}} \right)} \right|_\tau ^1 } = {\frac{1}{{1 - k}} \cdot \lim\limits_{\tau \to 0 + } \left( {{1^{ - k + 1}} - {\tau ^{ - k + 1}}} \right) } = {\frac{1}{{1 - k}} \cdot \lim\limits_{\tau \to 0 + } \left( {1 - {\tau ^{1 - k}}} \right).} \] Как видно из полученного выражения, возможны \(2\) случая:

• Если \(0 < k < 1,\) то \(\lim\limits_{\tau \to 0 + } {\tau ^{1 - k}} = 0\) и интеграл сходится;

• Если \(k > 1,\) то \(\lim\limits_{\tau \to 0 + } {\tau ^{1 - k}} = \lim\limits_{\tau \to 0 + } {\large\frac{1}{{{\tau ^{k - 1}}}}\normalsize} = \infty \) и интеграл расходится.

   Пример 9

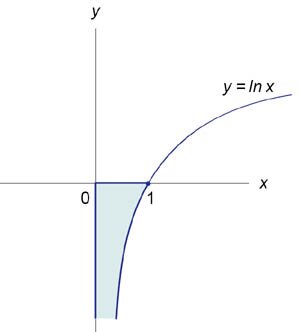
Найти площадь под кривой \(y = \ln x\) в интервале от \(x = 0\) до \(x =1.\) Данная область схематически изображена на рисунке \(1.\) Для нахождения площади этой бесконечной области нужно вычислить несобственный интеграл \[\int\limits_0^1 {\ln xdx} = \lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {\ln xdx} .\] Интегрируем по частям. Пусть \(u = \ln x,\) \(dv = dx.\) Тогда \(du = \large\frac{{dx}}{x}\normalsize,\;v = x.\) Следовательно, \[ {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {\ln xdx} } = {\lim\limits_{\tau \to 0 + } \left[ {\left. {\left( {x\ln x} \right)} \right|_\tau ^1 - \int\limits_\tau ^1 {x\frac{{dx}}{x}} } \right] } = {\lim\limits_{\tau \to 0 + } \left. {\left[ {x\ln x - x} \right]} \right|_\tau ^1 } = {\lim\limits_{\tau \to 0 + } \left[ {\left( {\ln 1 - 1} \right) - \left( {\tau \ln \tau - \tau } \right)} \right] } = {\left( {0 - 1} \right) - \lim\limits_{\tau \to 0 + } \left[ {\tau \left( {\ln \tau - 1} \right)} \right] } = { - 1 - \lim\limits_{\tau \to 0 + } \frac{{\ln \tau - 1}}{{\frac{1}{\tau }}}.} \] Для вычисления полученного предела используем правило Лопиталя. \[ {\lim\limits_{\tau \to 0 + } \frac{{\ln \tau - 1}}{{\frac{1}{\tau }}} } = {\lim\limits_{\tau \to 0 + } \frac{{\frac{1}{\tau }}}{{ - \frac{1}{{{\tau ^2}}}}} } = { - \lim\limits_{\tau \to 0 + } \frac{{{\tau ^2}}}{\tau } } = { - \lim\limits_{\tau \to 0 + } \tau = 0.} \] Таким образом, несобственный интеграл равен \[ {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {\ln xdx} } = { - 1 - \lim\limits_{\tau \to 0 + } \frac{{\ln \tau - 1}}{{\frac{1}{\tau }}} } = { - 1 - 0 = - 1.} \] Из рисунка видно, что площадь фигуры равна \(S = \left| {\lim\limits_{\tau \to 0 + } \int\limits_\tau ^1 {\ln xdx} } \right| = 1.\)

   Пример 10

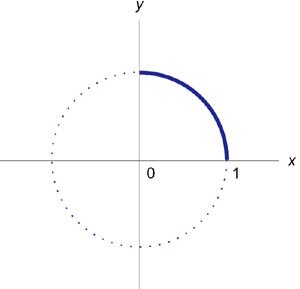
Вычислить периметр единичной окружности. Вычислим длину дуги окружности в первом квадранте между \(x = 0\) и \(x = 1\) и затем умножим результат на \(4.\)

Уравнение единичной окружности с центром в начале координат имеет вид \[{x^2} + {y^2} = 1.\] Дуга окружности в первой четверти (рисунок \(2\)) описывается функцией \[y = \sqrt {1 - {x^2}} ,\;\;0 \le x \le 1.\] Найдем производную данной функции. \[ {y' = \frac{d}{{dx}}\sqrt {1 - {x^2}} } = {\frac{{ - \cancel{2}x}}{{\cancel{2}\sqrt {1 - {x^2}} }} } = {\frac{{ - x}}{{\sqrt {1 - {x^2}} }}.} \] Длина дуги определяется формулой \(\int\limits_{x = \alpha }^{x = \beta } {\sqrt {1 + {{\left( {y'} \right)}^2}} dx} .\) Следовательно, \[ {\int\limits_0^1 {\sqrt {1 + {{\left( {\frac{{ - x}}{{\sqrt {1 - {x^2}} }}} \right)}^2}} dx} } = {\int\limits_0^1 {\sqrt {1 + \frac{{{x^2}}}{{1 - {x^2}}}} dx} } = {\int\limits_0^1 {\sqrt {\frac{{1 - \cancel{x^2} + \cancel{x^2}}}{{1 - {x^2}}}} dx} } = {\int\limits_0^1 {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} .} \] Теперь вычислим полученный несобственный интеграл \(\int\limits_0^1 {\large\frac{{dx}}{{\sqrt {1 - {x^2}} }}\normalsize}.\) \[ {\int\limits_0^1 {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} } = {\lim\limits_{\tau \to 0 + } \int\limits_0^{1 - \tau } {\frac{{dx}}{{\sqrt {1 - {x^2}} }}} } = {\lim\limits_{\tau \to 0 + } \left. {\left( {\arcsin x} \right)} \right|_0^{1 - \tau } } = {\lim\limits_{\tau \to 0 + } \left[ {\arcsin \left( {1 - \tau } \right) - \arcsin 0} \right] } = {\arcsin 1 - 0 = \frac{\pi }{2}.} \] Таким образом, периметр единичной окружности равен \({\large\frac{\pi }{2}\normalsize} \cdot 4 = 2\pi .\)