Нелинейный математический маятник

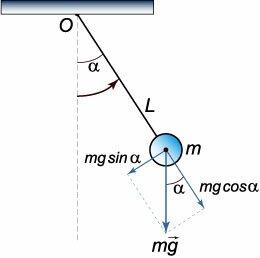
Математический маятник представляет собой идеальную модель, в которой материальная точка массой \(m\) подвешена на невесомой и нерастяжимой нити длиной \(L.\) В такой системе происходят периодические колебания, которые можно рассматривать как вращение маятника вокруг оси \(O\) (рисунок \(1\)). Динамика вращательного движения описывается дифференциальным уравнением \[\varepsilon = \frac{{{d^2}\alpha }}{{d{t^2}}} = \frac{M}{I},\] где \(\varepsilon\) − угловое ускорение, \(M\) − момент силы, вызывающий вращение, \(I\) − момент инерции тела относительно оси вращения.

В нашем случае момент силы определяется проекцией силы тяжести на тангенциальное направление, т.е. \[M = - mgL\sin \alpha .\] Знак минус означает, что при положительном угле поворота \(\alpha\) (против часовой стрелки) момент сил вызывает вращение в противоположном направлении.

Момент инерции маятника выражается формулой \[I = m{L^2}.\] Тогда уравнение динамики принимает вид: \[\require{cancel} {\frac{{{d^2}\alpha }}{{d{t^2}}} = \frac{{ - \cancel{m}g\cancel{L}\sin \alpha }}{{\cancel{m}{L^\cancel{2}}}} = - \frac{{g\sin \alpha }}{L},}\;\; {\Rightarrow \frac{{{d^2}\alpha }}{{d{t^2}}} + \frac{g}{L}\sin \alpha = 0.} \] В случае малых колебаний полагают \(\sin \alpha \approx \alpha.\) В результате возникает линейное дифференциальное уравнение \[ {\frac{{{d^2}\alpha }}{{d{t^2}}} + \frac{g}{L}\alpha = 0}\;\; {\text{или}\;\;\frac{{{d^2}\alpha }}{{d{t^2}}} + {\omega ^2}\alpha = 0,} \] где \(\omega = \sqrt {\large\frac{g}{L}\normalsize} \) − круговая частота колебаний.

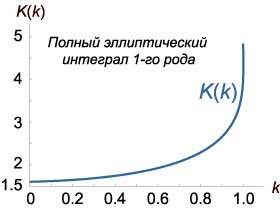
Период малых колебаний маятника описывается известной формулой \[T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{L}{g}} .\] Однако при увеличении амплитуды колебаний линейное приближение перестает быть справедливым. В этом случае для корректного описания колебательной системы нужно решать исходное нелинейное дифференциальное уравнение. Итак, пусть маятник описывается нелинейным дифференциальным уравнением второго порядка \[\frac{{{d^2}\alpha }}{{d{t^2}}} + \frac{g}{L}\sin \alpha = 0.\] Будем рассматривать колебания при начальных условиях \[\alpha \left( {t = 0} \right) = {\alpha _0},\;\;\frac{{d\alpha }}{{dt}}\left( {t = 0} \right) = 0.\] Угол \({\alpha _0}\) представляет собой амплитуду колебаний.

Порядок уравнения можно понизить, если подобрать подходящий интегрирующий множитель. Умножим данное уравнение на интегрирующий множитель \(\large\frac{{d\alpha }}{{dt}}\normalsize.\) Это приводит к уравнению \[ {\frac{{{d^2}\alpha }}{{d{t^2}}}\frac{{d\alpha }}{{dt}} + \frac{g}{L}\sin \alpha \frac{{d\alpha }}{{dt}} = 0,}\;\; {\Rightarrow \;\;\frac{d}{{dt}}\left[ {\frac{1}{2}{{\left( {\frac{{d\alpha }}{{dt}}} \right)}^2} - \frac{g}{L}\cos\alpha } \right] = 0.} \] После интегрирования получаем дифференциальное уравнение первого порядка: \[{\left( {\frac{{d\alpha }}{{dt}}} \right)^2} - \frac{{2g}}{L}\cos\alpha = C.\] С учетом начальных условий находим постоянную \(C:\) \[C = - \frac{{2g}}{L}\cos{\alpha _0}.\] Тогда уравнение принимает вид: \[{\left( {\frac{{d\alpha }}{{dt}}} \right)^2} = \frac{{2g}}{L}\left( {\cos\alpha - \cos{\alpha _0}} \right).\] Далее применим тригонометрическую формулу двойного угла \[\cos\alpha = 1 - 2\,{\sin ^2}\frac{\alpha }{2},\] что приводит к следующему дифференциальному уравнению: \[ {{\left( {\frac{{d\alpha }}{{dt}}} \right)^2} = \frac{{4g}}{L}\left( {{{\sin }^2}\frac{{{\alpha _0}}}{2} - {{\sin }^2}\frac{\alpha }{2}} \right),}\;\; {\Rightarrow \frac{{d\alpha }}{{dt}} = 2\sqrt {\frac{g}{L}} \sqrt {{{\sin }^2}\frac{{{\alpha _0}}}{2} - {{\sin }^2}\frac{\alpha }{2}} .} \] Интегрируя это уравнение, получаем \[\int {\frac{{d\left( {\frac{\alpha }{2}} \right)}}{{\sqrt {{{\sin }^2}\frac{{{\alpha _0}}}{2} - {{\sin }^2}\frac{\alpha }{2}} }}} = \sqrt {\frac{g}{L}} \int {dt} .\] Обозначим \(\sin {\large\frac{{{\alpha _0}}}{2}\normalsize} = k\) и введем новую переменную \(\theta\) вместо угла \(\alpha:\) \[\sin \frac{\alpha }{2} = \sin \frac{{{\alpha _0}}}{2}\sin \theta = k\sin \theta .\] Тогда \[ {d\left( {\sin \frac{\alpha }{2}} \right) = \cos \frac{\alpha }{2}d\left( {\frac{\alpha }{2}} \right) } = {\sqrt {1 - {{\sin }^2}\frac{\alpha }{2}} d\left( {\frac{\alpha }{2}} \right) } = {\sqrt {1 - {k^2}\,{{\sin }^2}\theta } \,d\left( {\frac{\alpha }{2}} \right) } = {k\cos \theta d\theta .} \] Отсюда следует, что \[d\left( {\frac{\alpha }{2}} \right) = \frac{{k\cos \theta d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } }}.\] В новых обозначениях наше уравнение записывается как \[ {\int {\frac{{k\cos \theta d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } \sqrt {{k^2} - {k^2}\,{{\sin }^2}\theta } }}} = \sqrt {\frac{g}{L}} \int {dt} ,}\;\; {\Rightarrow \int {\frac{{\cancel{k\cos \theta} d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta }\,\cancel{k\cos \theta} }}} = \sqrt {\frac{g}{L}} \int {dt} ,}\;\; {\Rightarrow \int {\frac{{d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } }}} = \sqrt {\frac{g}{L}} \int {dt} .} \] Обсудим пределы интегрирования. Прохождение маятником дуги от нижней точки \(\alpha = 0\) до максимального отклонения \(\alpha = {\alpha_0}\) соответствует четверти периода колебаний \(\large\frac{T}{4}\normalsize.\) Из соотношения между углами \(\alpha\) и \(\theta\) следует, что при \(\alpha = {\alpha_0}\) должно быть \(\sin \theta = 1\) или \(\theta = {\large\frac{\pi}{2}\normalsize}.\) Поэтому получаем следующее выражение для периода колебаний маятника: \[ {\sqrt {\frac{g}{L}} \frac{T}{4} = \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } }}} }\;\; {\text{или}\;\;T = 4\sqrt {\frac{L}{g}} \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } }}} .} \] Интеграл в правой части не выражается через элементарные функции. Он представляет собой так называемый полный эллиптический интеграл \(1\)-го рода: \[K\left( k \right) = \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\frac{{d\theta }}{{\sqrt {1 - {k^2}\,{{\sin }^2}\theta } }}} .\] Функция \(K\left( k \right)\) вычисляется в большинстве математических пакетов. Ее график приведен выше на рисунке \(2.\) Функцию \(K\left( k \right)\) можно представить также в виде степенного ряда: \[ {K\left( k \right) = \frac{\pi }{2}\left\{ {1 + {{\left( {\frac{1}{2}} \right)}^2}{k^2} + {{\left( {\frac{{1 \cdot 3}}{{2 \cdot 4}}} \right)}^2}{k^4} + {{\left( {\frac{{1 \cdot 3 \cdot 5}}{{2 \cdot 4 \cdot 6}}} \right)}^2}{k^6} + \ldots } \right.} {\left. {\;+ {{\left[ {\frac{{\left( {2n - 1} \right)!!}}{{\left( {2n} \right)!!}}} \right]}^2}{k^{2n}} + \ldots } \right\},} \] где двойные факториалы \({\left( {2n - 1} \right)!!}\) и \({\left( {2n} \right)!!}\) обозначают произведение, соответственно, натуральных нечетных и четных чисел.

Заметим, что если мы ограничимся нулевым членом разложения, полагая \(K\left( k \right) \approx {\large\frac{\pi }{2}\normalsize},\) то получим известную формулу для периода малых колебаний маятника: \[{T_0} = 4\sqrt {\frac{L}{g}} K\left( k \right) \approx 4\sqrt {\frac{L}{g}} \frac{\pi }{2} = 2\pi \sqrt {\frac{L}{g}} .\] Последующие члены ряда при \(n \ge 1\) как раз позволяют учесть ангармонизм колебаний маятника и нелинейную зависимость периода \(T\) от амплитуды колебаний \({\alpha_0}.\)

   Пример

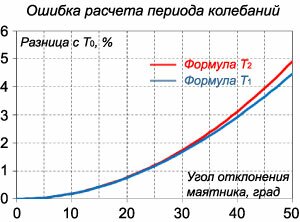
Оценить ошибку в расчете периода колебаний математического маятника в случае использования простейшей формулы \({T_0} = 2\pi \sqrt {\large\frac{L}{g}\normalsize} \) при различной амплитуде колебаний \({\alpha_0}.\)
Воспользуемся решением более общего нелинейного уравнения колебаний маятника, в котором выражение для периода \(T\) представляется в виде ряда. С учетом члена \(n = 1\) формула \(T\left( {{\alpha _0}} \right)\) выглядит так: \[ {{T_1}\left( {{\alpha _0}} \right) = 4\sqrt {\frac{L}{g}} K\left( k \right) } = {4\sqrt {\frac{L}{g}} K\left( {\sin {\alpha _0}} \right) } = {4\sqrt {\frac{L}{g}} \left[ {\frac{\pi }{2}\left( {1 + \frac{1}{4}{{\sin }^2}\frac{{{\alpha _0}}}{2}} \right)} \right] } = {{T_0}\left( {1 + \frac{1}{4}{{\sin }^2}\frac{{{\alpha _0}}}{2}} \right),} \] где \({T_0}\) − период колебаний, вычисляемый по стандартной формуле \[{T_0} = 2\pi \sqrt {\frac{L}{g}} .\] Таким образом, слагаемое \({{\large\frac{1}{4}\normalsize} {{\sin }^2}{\large\frac{{{\alpha _0}}}{2}\normalsize}}\) сразу же показывает отклонение от стандартной формулы (в долях единицы) в зависимости от угла \({\alpha_0}.\)

Аналогичным образом учтем вклад последующих членов ряда при \(n = 2\) и \(n = 3.\) Соответствующие формулы имеют вид: \[{T_2}\left( {{\alpha _0}} \right) = {T_0}\left( {1 + \frac{1}{4}{{\sin }^2}\frac{{{\alpha _0}}}{2} + \frac{9}{{64}}{{\sin }^4}\frac{{{\alpha _0}}}{2}} \right),\] \[ {{T_3}\left( {{\alpha _0}} \right) = {T_0}\left( {1 + \frac{1}{4}{{\sin }^2}\frac{{{\alpha _0}}}{2} + \frac{9}{{64}}{{\sin }^4}\frac{{{\alpha _0}}}{2}} \right.} {\left. {\;+\;\frac{{225}}{{2304}}{{\sin }^6}\frac{{{\alpha _0}}}{2}} \right).} \] Представленные на рисунке \(3\) графики показывают значение выражения в квадратных скобках для функций \({T_1}\) и \({T_2}\) (в процентах), т.е. фактически дают ошибку в определении периода колебаний при использовании стандартной формулы \({T_0}\) по сравнению с более точными приближениями. Видно, что степенной ряд хорошо сходится, и в диапазоне углов до \({\alpha_0} = 20^{\circ}\) вполне можно ограничиться в разложении первым членом ряда \(n = 1,\) чтобы обеспечить точность расчета около \(1\%.\)