Натуральный логарифм

Логарифм по основанию \(e\) (\(e\) - трансцендентное число, приближенно равное \(2.718281828\ldots\)) называется натуральным логарифмом. Натуральный логарифм числа x обозначается \(\ln x\). Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.

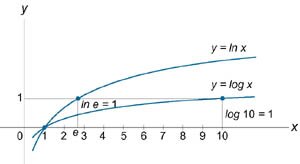
Пусть число \(a\) является основанием логарифма (\(a > 0\), \(a \ne 1\)), и пусть задана логарифмическая функция \[y = {\log _a}x.\] Отсюда следует, что \[{a^y} = x.\] Взяв натуральный логарифм от левой и правой части, получаем \[\ln {a^y} = \ln x,\;\; {\Rightarrow y\ln a = \ln x,}\;\; {\Rightarrow y = \frac{1}{{\ln a}}\ln x,}\;\; {\Rightarrow {\log _a}x = \frac{{\ln x}}{{\ln a}}.} \] Последняя формула выражает произвольный логарифм числа \(x\) по основанию \(a\) через натуральный логарифм этого числа. Полагая \(x = e\), можно записать \[{\log _a}e = \frac{1}{{\ln a}}\ln e = \frac{1}{{\ln a}}.\] Если \(a = 10\), то получаем десятичный логарифм: \[{\log _{10}}x = \lg x = M\,{\ln x} ,\;\; {\text{где}\;\;M = \frac{1}{{\ln a}} = \lg e \approx 0.43429 \ldots } \] Обратное соотношение имеет вид: \[\ln x = \frac{1}{M}\lg x,\;\; {\text{где}\;\;\frac{1}{M} = \ln 10 \approx 2.30258 \ldots } \] Графики функций \(y = \ln x\) и \(y = \lg x\) показаны на рисунке 1.

   Пример 1

Вычислить \(\ln \large\frac{1}{{\sqrt e }}\normalsize\). \[\ln \frac{1}{{\sqrt e }} = \ln {e^{ - \large\frac{1}{2}\normalsize}} = - \frac{1}{2}\ln e = - \frac{1}{2}.\]

   Пример 2

Записать в виде одного логарифма \(\large\frac{1}{3}\normalsize\ln \left( {x - 1} \right) - {\large\frac{1}{2}\normalsize\ln \left( {x + 1} \right)} + {2\ln x}\). \[\frac{1}{3}\ln \left( {x - 1} \right) - \frac{1}{2}\ln \left( {x + 1} \right) + 2\ln x = {\ln {\left( {x - 1} \right)^{\large\frac{1}{3}\normalsize}} - \ln {\left( {x + 1} \right)^{\large\frac{1}{2}\normalsize}} + \ln {x^2} } = {\ln \sqrt[\large 3\normalsize]{{x - 1}} - \ln \sqrt {x + 1} + \ln {x^2} } = {\ln \frac{{{x^2}\sqrt[3]{{x - 1}}}}{{\sqrt {x + 1} }}.} \]

   Пример 3

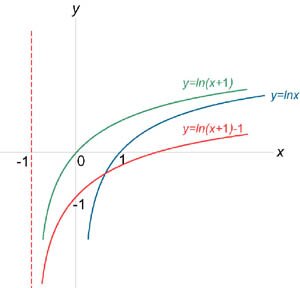
Схематически изобразить график функции \(y = \ln \left( {x + 1} \right) - 1\). График функции \(y = \ln \left( {x + 1} \right) - 1\) получается в результате сдвига графика функции \(y = \ln x\) на одну единицу влево (при этом мы получаем функцию \(y = \ln \left( {x + 1} \right)\)) и на одну единицу вниз (рисунок 2).

   Пример 4

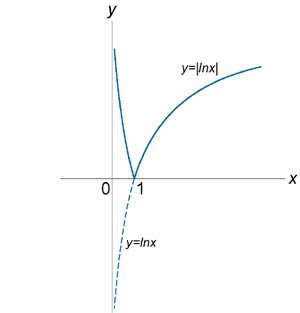
Схематически изобразить график функции \(y = \left| {\ln x} \right|\). График искомой функции (рисунок 3) получается в результате следующих преобразований. Часть графика функции \(y = \left| {\ln x} \right|\), лежащая в области \(x \ge 1\), совпадает с графиком функции \(y = \ln x\). Остальная часть, соответствующая \(y < 0\) (при \(0 < x < 1\)), отражается относительно оси \(Ox\) в верхнюю полуплоскость.

   Пример 5

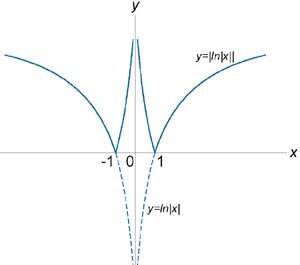
Схематически изобразить график функции \(y = \left| {\ln \left| x \right|} \right|\). Сначала мы построим график функции \(y = \left| {\ln x} \right|\), как описано в предыдущем примере. Затем отразим график этой функции относительно оси \(Oy\) в левую полуплоскость. Совокупность этих графиков и представляет собой график искомой функции \(y = \left| {\ln \left| x \right|} \right|\) (рисунок 4).