Наибольшее и наименьшее значения функции

Рассмотрим функцию \(y = f\left( x \right),\) которая является непрерывной на отрезке \(\left[ {a,b} \right].\) Если существует точка \({x_0} \in \left[ {a,b} \right],\) такая, что для всех \(x \in \left[ {a,b} \right]\) выполняется неравенство \(f\left( x \right) \le f\left( {{x_0}} \right),\) то говорят, что функция \(f\left( x \right)\) принимает в точке \({x_0}\) наибольшее (максимальное) значение на отрезке \(\left[ {a,b} \right].\)

Наибольшее значение функции \(f\left( x \right)\) на отрезке \(\left[ {a,b} \right]\) является одновременно точной верхней гранью множества значений функции на этом отрезке и обозначается как \[ {f\left( {{x_0}} \right) = \max\limits_{x \in \left[ {a,b} \right]} f\left( x \right) } = {\sup\limits_{x \in \left[ {a,b} \right]} f\left( x \right).} \] Аналогично, если существует точка \({x_0} \in \left[ {a,b} \right],\) такая, что для всех \(x \in \left[ {a,b} \right]\) выполняется неравенство \(f\left( x \right) \ge f\left( {{x_0}} \right),\) то функция \(f\left( x \right)\) принимает в точке \({x_0}\) наименьшее (минимальное) значение на отрезке \(\left[ {a,b} \right].\)

Наименьшее значение функции \(f\left( x \right)\) на отрезке \(\left[ {a,b} \right]\) является также точной нижней гранью множества значений функции на этом отрезке и записывается в виде \[ {f\left( {{x_0}} \right) = \min\limits_{x \in \left[ {a,b} \right]} f\left( x \right) } = {\inf\limits_{x \in \left[ {a,b} \right]} f\left( x \right).} \] Введенные понятия характеризуют поведение функции на конечном отрезке, в отличие от локального экстремума, который описывает свойства функции в малой окрестности точки. Поэтому наибольшее и наименьшее значения функции на отрезке часто называют также глобальным (абсолютным) максимумом или, соответственно, глобальным минимумом. Согласно второй теореме Вейерштрасса о непрерывных функциях, если функция \(f\left( x \right)\) непрерывна на отрезке \(\left[ {a,b} \right],\) то она достигает на нем своей точной верхней и нижней грани.

Доказательство этой теоремы опирается на первую теорему Вейерштрасса, которая формулируется так:

Если функция \(f\left( x \right)\) непрерывна на отрезке \(\left[ {a,b} \right],\) то она ограничена на нем, т.е. существует число \(M,\) такое, что \(\left| {f\left( x \right)} \right| \le M\) для всех \(x \in \left[ {a,b} \right].\)

Возвращаясь ко второй теореме Вейерштрасса, обозначим через \(M\) точную верхнюю грань множества значений функции (или наибольшее значение функции) на отрезке \(\left[ {a,b} \right].\) Предположим противное − что точная верхняя грань не достигается, т.е. допустим, что \[f\left( x \right) < M\;\forall \;x \in \left[ {a,b} \right].\] Рассмотрим вспомогательную функцию: \[\varphi \left( x \right) = \frac{1}{{M - f\left( x \right)}}.\] Поскольку знаменатель не равен нулю, то функция \(\varphi \left( x \right)\) также непрерывна на \(\left[ {a,b} \right]\) и, следовательно, по первой теореме Вейерштрасса ограничена на этом отрезке: \(\varphi \left( x \right) \le L,\) где \(L > 0.\) Отсюда получаем, что \[ {\varphi \left( x \right) \le L,}\;\; {\Rightarrow \frac{1}{{M - f\left( x \right)}} \le L,}\;\; {\Rightarrow M - f\left( x \right) \ge \frac{1}{L},}\;\; {\Rightarrow f\left( x \right) \le M - \frac{1}{L}\;\forall \;x \in \left[ {a,b} \right].} \] Другими словами, число \(M - \large\frac{1}{L}\normalsize\) будет являться точной верхней гранью функции \(f\left( x \right)\), что противоречит условию. (По условию, точная верхняя грань функции равна \(M.\))

Таким же образом можно доказать, что непрерывная на отрезке \(\left[ {a,b} \right]\) функция достигает свой точной нижней грани (или наименьшего значения).

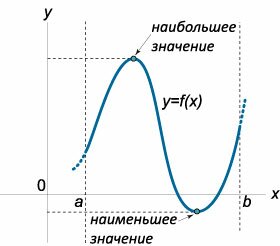
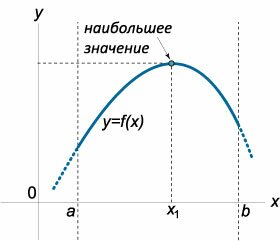
Итак, согласно второй теореме Вейерштрасса, непрерывная на отрезке функция всегда достигает своего наибольшего и наименьшего значения на этом отрезке. Пусть функция \(y = f\left( x \right)\) непрерывна на отрезке \(\left[ {a,b} \right].\)

Если функция на этом отрезке имеет локальные максимумы в точках \({x_1},{x_2}, \ldots ,{x_n},\) то наибольшее значение функции \(f\left( x \right)\) на отрезке \(\left[ {a,b} \right]\) равно наибольшему из чисел \[f\left( a \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right), \ldots ,f\left( {{x_n}} \right),f\left( b \right).\] Аналогично, если функция на этом отрезке имеет локальные минимумы в точках \({{\bar x}_1},{{\bar x}_2}, \ldots ,{{\bar x}_k},\) то наименьшее значение функции \(f\left( x \right)\) на отрезке \(\left[ {a,b} \right]\) равно наименьшему из чисел \[f\left( a \right),f\left( {{{\bar x}_1}} \right),f\left( {{{\bar x}_2}} \right), \ldots ,f\left( {{{\bar x}_k}} \right),f\left( b \right).\] Таким образом, наибольшее (наименьшее) значения функции могут достигаться либо на границе отрезка (рисунок \(1\)), либо в точках локального экстремума внутри отрезка (рисунок \(2\)). 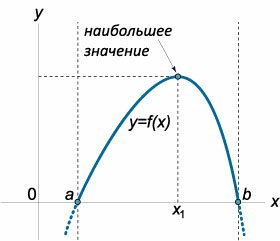Если внутри отрезка \(\left[ {a,b} \right]\) существует единственная точка экстремума \({x_1}\) и эта точка является локальным максимумом (минимумом), то в ней функция принимает наибольшее (наименьшее) значение (рисунок \(3\)). 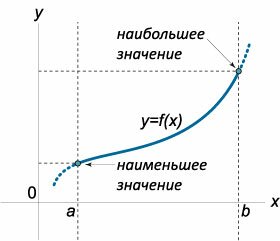Если функция \(y = f\left( x \right)\) не имеет критических точек на отрезке \(\left[ {a,b} \right],\) то функция принимает наименьшее значение на одном конце отрезка и наибольшее значение − на другом (рисунок \(4\)). На практике часто встречается случай, когда на отрезке \(\left[ {a,b} \right]\) задана дифференцируемая и положительно определенная функция \(f\left( x \right) > 0,\) причем в граничных точках она равна нулю: \(f\left( a \right) = f\left( b \right) = 0.\) Если такая функция имеет единственную стационарную точку \({x_1}\) (где \(f'\left( {{x_1}} \right) = 0,\)) то эта точка является не только локальным максимумом функции, но и ее наибольшим значением на отрезке \(\left[ {a,b} \right].\) (рисунок \(5\)). В примерах \(1-10\) найти наибольшее и наименьшее значения функции на заданном отрезке.

   Пример 1

\[f\left( x \right) = {x^2} - 2x + 5,\;\;x \in \left[ { - 1,4} \right].\] Данная функция определена и дифференцируема при всех \(x \in \mathbb{R}.\) Определим стационарные точки: \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow {\left( {{x^2} - 2x + 5} \right)^\prime } = 0,}\;\; {\Rightarrow 2x - 2 = 0,}\;\; {\Rightarrow x = 1.} \] Найденная точка локального экстремума принадлежит интервалу \(\left( { - 1,4} \right).\) Вычислим значения функции в точке \(x = 1\) и на концах отрезка: \[ {f\left( 1 \right) = {1^2} - 2 \cdot 1 + 5 = 4,}\;\;\; {f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2 \cdot \left( { - 1} \right) + 5 = 8,}\;\;\; {f\left( 4 \right) = {4^2} - 2 \cdot 4 + 5 = 13.} \] Следовательно, наибольшее значение функции равно \(f\left( 4 \right) = 13,\) а наименьшее значение составляет \(f\left( 1 \right) = 4.\)

   Пример 2

\[f\left( x \right) = x + \frac{2}{x},\;\;x \in \left[ {0.5,2} \right].\] Данная функция не определена при \(x = 0,\) но эта точка не входит в заданный отрезок. Дифференцируя функцию, находим точки экстремума: \[ {f'\left( x \right) = {\left( {x + \frac{2}{x}} \right)^\prime } } = {1 - \frac{2}{{{x^2}}};} \] \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow 1 - \frac{2}{{{x^2}}} = 0,}\;\; {\Rightarrow \frac{2}{{{x^2}}} = 1,}\;\; {\Rightarrow {x^2} = 2,}\;\; {\Rightarrow x = \pm \sqrt 2 .} \] В отрезок \(\left[ {0.5,2} \right]\) попадает лишь точка \(x = \sqrt 2 .\) Вычислим значения функции в точке экстремума \(x = \sqrt 2\) и в граничных точках отрезка: \[ {f\left( {\sqrt 2 } \right) = \sqrt 2 + \frac{2}{{\sqrt 2 }} = 2\sqrt 2 \approx 2.83;}\;\;\; {f\left( {0.5} \right) = 0.5 + \frac{2}{{0.5}} = 4.5;}\;\;\; {f\left( 2 \right) = 2 + \frac{2}{2} = 3.} \] Итак, наибольшее значение функции на данном отрезке равно \(4.5\) в точке \(x = 0.5,\) и наименьшее значение составляет \(2.83\) при \(x = \sqrt 2.\)

   Пример 3

\[f\left( x \right) = 3{x^4} - 6{x^2} + 2,\;\;x \in \left[ { - 2,2} \right].\] Данная функция определена и дифференцируема на всей числовой оси. В таком случае все локальные экстремумы находятся из уравнения \(f'\left( x \right) = 0:\) \[ {f'\left( x \right) = {\left( {3{x^4} - 6{x^2} + 2} \right)^\prime } } = {12{x^3} - 12x } = {12x\left( {{x^2} - 1} \right) } = {12x\left( {x - 1} \right)\left( {x + 1} \right);} \] \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow 12x\left( {x - 1} \right)\left( {x + 1} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = - 1,\;{x_3} = 1.} \] Как видно, функция имеет три локальных экстремума, причем все эти точки попадают в заданный отрезок \(\left[ { - 2,2} \right].\) Рассчитаем значения функции в точках экстремума и на концах отрезка: \[ {f\left( 0 \right) = 3 \cdot {0^4} - 6 \cdot {0^2} + 2 = 2;}\;\;\; {f\left( { - 1} \right) = 3 \cdot {\left( { - 1} \right)^4} - 6 \cdot {\left( { - 1} \right)^2} + 2 = - 1;}\;\;\; {f\left( { - 2} \right) = 3 \cdot {\left( { - 2} \right)^4} - 6 \cdot {\left( { - 2} \right)^2} + 2 = 26.} \] Поскольку функция является четной, то следовательно: \[ {f\left( 1 \right) = f\left( { - 1} \right) = - 1,}\;\;\; {f\left( 2 \right) = f\left( { - 2} \right) = 26.} \] Итак, функция принимает наименьшее значение \(-1\) сразу в двух точках: при \(x = -1\) и \(x = 1.\) Наибольшее значение \(26\) достигается также в двух точках: при \(x = -2\) и \(x = 2.\) Схематический график функции показан на рисунке \(7\).

   Пример 4

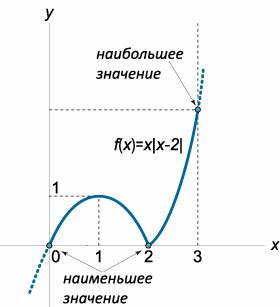
\[f\left( x \right) = x\left| {x - 2} \right|,\;\;x \in \left[ {0,3} \right].\] Раскрывая модуль, представим данную функцию в виде \[ f(x) = {\begin{cases} - x\left( {x - 2} \right), & x < 2 \\ x\left( {x - 2} \right), & x \ge 2 \end{cases},}\;\; {\Rightarrow f(x) = \begin{cases} - {x^2} + 2x, & x < 2 \\ {x^2} - 2x, & x \ge 2 \end{cases}.} \] Как видно, функция состоит из двух квадратичных функций: \({f_1}\left( x \right) = - {x^2} + 2x\) и \({f_2}\left( x \right) = {x^2} - 2x.\) В точке \(x = 2,\) где соединяются обе ветви, график функции имеет излом (рисунок \(8\)), т.е. в этой точке производной не существует.

Найдем другие критические точки обеих ветвей функции: \[ {{f'_1}\left( x \right) = 0,}\;\; {\Rightarrow {\left( { - {x^2} + 2x} \right)^\prime } = 0,}\;\; {\Rightarrow - 2x + 2 = 0,}\;\; {\Rightarrow x = 1;} \] \[ {{f'_2}\left( x \right) = 0,}\;\; {\Rightarrow {\left( {{x^2} - 2x} \right)^\prime } = 0,}\;\; {\Rightarrow 2x - 2 = 0,}\;\; {\Rightarrow x = 1.} \] Здесь корень \(x = 1\) имеет смысл лишь для первой ветви решений, которая существует при \(x < 2.\)

Определим значения функции в найденных критических точках \(x = 1,\) \(x = 2\) и на концах отрезка при \(x = 0\) и \(x = 3:\) \[ {f\left( 0 \right) = 0 \cdot \left| {0 - 2} \right| = 0,}\;\;\; {f\left( 1 \right) = 1 \cdot \left| {1 - 2} \right| = 1,}\;\;\; {f\left( 2 \right) = 2 \cdot \left| {2 - 2} \right| = 0,}\;\;\; {f\left( 3 \right) = 3 \cdot \left| {3 - 2} \right| = 3.}\;\;\; \] Отсюда видно, что функция принимает наименьшее значение \(y = 0\) в двух точках: при \(x = 0\) и \(x = 2.\) Наибольшее значение составляет \(f\left( 3 \right) = 3.\)

   Пример 5

\[f\left( x \right) = \sqrt {3 - 2x} ,\;\;x \in \left[ { - 3,1} \right].\] Функция определена при условии \[ {3 - 2x \ge 0,}\;\; {\Rightarrow 2x \le 3,}\;\; {\Rightarrow x \le \frac{3}{2}.} \] Заданный в условии отрезок попадает в область определения функции. На этом отрезке функция дифференцируема и ее экстремумы (если они существуют) определяются из условия \(f'\left( x \right) = 0.\) Найдем производную: \[\require{cancel} {f'\left( x \right) = {\left( {\sqrt {3 - 2x} } \right)^\prime } } = {\frac{{{{\left( {3 - 2x} \right)}^\prime }}}{{2\sqrt {3 - 2x} }} } = {\frac{{ - \cancel{2}}}{{\cancel{2}\sqrt {3 - 2x} }} } = { - \frac{1}{{\sqrt {3 - 2x} }}.} \] Отсюда следует, что уравнение \(f'\left( x \right) = 0\) не имеет решений, т.е. функция не имеет локальных экстремумов. Так как производная отрицательна, то функция \(f\left( x \right)\) монотонно убывает на отрезке \(\left[ { - 3,1} \right].\) Вычисляя значение функции в граничных точках: \[ {f\left( { - 3} \right) = \sqrt {3 - 2 \cdot \left( { - 3} \right)} = 3,}\;\;\; {f\left( 1 \right) = \sqrt {3 - 2 \cdot 1} = 1,} \] находим, что наибольшее значение равно \(3\) при \(x = -3,\) а наименьшее значение равно \(1\) при \(x = 1.\)

   Пример 6

\[f\left( x \right) = \frac{{{x^2}}}{{{2^x}}},\;\;x \in \left[ { - 1,3} \right].\] Видно, что функция определена и дифференцируема при всех \(x \in \mathbb{R}.\) Поэтому все критические точки находятся из условия \(f'\left( x \right) = 0:\) \[ {f'\left( x \right) = {\left( {\frac{{{x^2}}}{{{2^x}}}} \right)^\prime } } = {\frac{{{{\left( {{x^2}} \right)}^\prime }{2^x} - {x^2}{{\left( {{2^x}} \right)}^\prime }}}{{{{\left( {{2^x}} \right)}^2}}} } = {\frac{{2x \cdot {2^x} - {x^2} \cdot {2^x}\ln 2}}{{{{\left( {{2^x}} \right)}^2}}} } = {\frac{{\cancel{2^x}x\left( {2 - x\ln 2} \right)}}{{\cancel{2^x} \cdot {2^x}}} } = {\frac{{x\left( {2 - x\ln 2} \right)}}{{{2^x}}};} \] \[ {f'\left( x \right) = 0,}\;\; {\Rightarrow \frac{{x\left( {2 - x\ln 2} \right)}}{{{2^x}}} = 0,}\;\; {\Rightarrow x\left( {2 - x\ln 2} \right) = 0,}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = \frac{2}{{\ln 2}} \approx 2,885.} \] Найдено \(2\) точки локального экстремума: \({x_1} = 0\) и \({x_2} = \large\frac{2}{{\ln 2}}\normalsize.\) Вычислим значения функции в этих точках и на границах отрезка и определим наибольшее и наименьшее значения функции на заданном отрезке: \[ {f\left( 0 \right) = \frac{{{0^2}}}{{{2^0}}} = 0;}\;\;\; {f\left( {\frac{2}{{\ln 2}}} \right) = \frac{{{{\left( {\frac{2}{{\ln 2}}} \right)}^2}}}{{{2^{\frac{2}{{\ln 2}}}}}} } {\approx \frac{{{{\left( {2,885} \right)}^2}}}{{{2^{2,885}}}} \approx 1,127;}\;\;\; {f\left( { - 1} \right) = \frac{{{{\left( { - 1} \right)}^2}}}{{{2^{ - 1}}}} = 2;}\;\;\; {f\left( 3 \right) = \frac{{{3^2}}}{{{2^3}}} = 1,125.} \] Следовательно, наибольшее значение функции равно \(2\) при \(x = -1,\) наименьшее значение равно \(0\) при \(x = 0.\)

   Пример 7

\[f\left( x \right) = \sqrt[\large x\normalsize]{x},\;\;x \in \left[ {2,3} \right].\] Данная функция определена и дифференцируема при \(x > 0.\) Ее производную можно найти с помощью логарифмического дифференцирования: \[ {y = \sqrt[\large x\normalsize]{x} = {x^{\large\frac{1}{x}\normalsize}},}\;\; {\Rightarrow \ln y = \ln {x^{\large\frac{1}{x}\normalsize}},}\;\; {\Rightarrow \ln y = \frac{1}{x}\ln x,}\;\; {\Rightarrow {\left( {\ln y} \right)^\prime } = {\left( {\frac{1}{x}\ln x} \right)^\prime },}\;\; {\Rightarrow \frac{{y'}}{y} = {\left( {\frac{1}{x}} \right)^\prime }\ln x + \frac{1}{x}{\left( {\ln x} \right)^\prime },}\;\; {\Rightarrow \frac{{y'}}{y} = \left( { - \frac{1}{{{x^2}}}} \right) \cdot \ln x + \frac{1}{x} \cdot \frac{1}{x},}\;\; {\Rightarrow \frac{{y'}}{y} = \frac{1}{{{x^2}}}\left( {1 - \ln x} \right),}\;\; {\Rightarrow y' = {x^{\large\frac{1}{x}\normalsize}} \cdot \frac{1}{{{x^2}}}\left( {1 - \ln x} \right),}\;\; {\Rightarrow y' = {x^{\large\frac{1}{x}\normalsize - 2}}\left( {1 - \ln x} \right).} \] Приравнивая производную нулю, определим критические (точнее стационарные) точки функции: \[ {y' = 0,}\;\; {\Rightarrow {x^{\large\frac{1}{x}\normalsize - 2}}\left( {1 - \ln x} \right) = 0,}\;\; {\Rightarrow 1 - \ln x = 0,}\;\; {\Rightarrow \ln x = 1,}\;\; {\Rightarrow x = e.} \] Вычислим теперь значения функции в критической точке \(x = e\) (которая попадает в заданный отрезок) и на границах отрезка − в точках \(x = 2\) и \(x = 3:\) \[ {f\left( e \right) = {e^{\large\frac{1}{e}\normalsize}} \approx 1,445;}\;\;\; {f\left( 2 \right) = {2^{\large\frac{1}{2}\normalsize}} = \sqrt 2 \approx 1,414;}\;\;\; {f\left( 3 \right) = {3^{\large\frac{1}{3}\normalsize}} = \sqrt[\large 3\normalsize]{3} \approx 1,442.} \] Итак, наименьшее значение функции равно \(f\left( 2 \right) \approx 1,414,\) а наибольшее значение, соответственно, равно \(f\left( e \right) \approx 1,445.\)

   Пример 8

\[f\left( x \right) = {\cos ^2}x - 2\sin x,\;\;x \in \left[ {0,2\pi } \right].\] Производная функции имеет вид: \[ {f'\left( x \right) = {\left( {{{\cos }^2}x - 2\sin x} \right)^\prime } } = {2\cos x{\left( {\cos x} \right)^\prime } - 2\cos x } = { - 2\cos x\sin x - 2\cos x } = { - 2\cos x\left( {1 + \sin x} \right).} \] Найдем критические точки, полагая \(f'\left( x \right) = 0:\) \[f'\left( x \right) = 0,\;\; \Rightarrow - 2\cos x\left( {1 + \sin x} \right) = 0.\]

1. \( {2\cos x = 0,}\;\; {\Rightarrow \cos x = 0,}\;\; {\Rightarrow x = \large\frac{\pi }{2}\normalsize + \pi n,\;n \in \mathbb{Z};} \)

2. \( {1 + \sin x = 0,}\;\; {\Rightarrow \sin x = - 1,}\;\; {\Rightarrow x = \large\frac{{3\pi }}{2}\normalsize + 2\pi k,\;k \in \mathbb{Z}.} \)

В заданный отрезок \(\left[ {0,2\pi } \right]\) попадают следующие критические точки: \[x = \frac{\pi }{2},\;\;x = \frac{{3\pi }}{2}.\] Теперь достаточно вычислить значения функции в этих точках и на краях отрезка, чтобы определить наибольшее и наименьшее значения: \[ {f\left( {\frac{\pi }{2}} \right) } = {{\cos ^2}\frac{\pi }{2} - 2\sin \frac{\pi }{2} } = {0 - 2 = - 2;} \] \[ {f\left( {\frac{{3\pi }}{2}} \right) } = {{\cos ^2}\left( {\frac{{3\pi }}{2}} \right) - 2\sin \frac{{3\pi }}{2} } = {0 + 2 = 2;} \] \[f\left( 0 \right) = {\cos ^2}0 - 2\sin 0 = 1 - 0 = 1.\] Функция имеет период \(2\pi.\) Поэтому \(f\left( {2\pi } \right) = f\left( 0 \right) = 1.\)

Таким образом наибольшее значение функции на отрезке \(\left[ {0,2\pi } \right]\) равно \(2\) при \(x = \large\frac{{3\pi }}{2}\normalsize,\) а наименьшее − равно \(-2\) при \(x = \large\frac{{\pi }}{2}\normalsize.\)

   Пример 9

\[f\left( x \right) = \arctan \frac{{1 - x}}{{1 + x}},\;\;x \in \left[ {0,1} \right].\] Очевидно, функция определена всюду на числовой оси, кроме точки \(x = -1,\) которая не попадает в заданный интервал. Находим производную: \[ {f'\left( x \right) = {\left( {\arctan \frac{{1 - x}}{{1 + x}}} \right)^\prime } } = {\frac{1}{{1 + {{\left( {\frac{{1 - x}}{{1 + x}}} \right)}^2}}} \cdot {\left( {\frac{{1 - x}}{{1 + x}}} \right)^\prime } } = {\frac{{{{\left( {1 + x} \right)}^2}}}{{{{\left( {1 + x} \right)}^2} + {{\left( {1 - x} \right)}^2}}} } {\cdot \frac{{{{\left( {1 - x} \right)}^\prime }\left( {1 + x} \right) - \left( {1 - x} \right){{\left( {1 + x} \right)}^\prime }}}{{{{\left( {1 + x} \right)}^2}}} } = {\frac{{ - \left( {1 + x} \right) - \left( {1 - x} \right)}}{{\color{maroon}{1} + \cancel{\color{red}{2x}} + \color{blue}{x^2} + \color{maroon}{1} - \cancel{\color{red}{2x}} + \color{blue}{x^2}}} } = {\frac{{ - \color{green}{1} - \cancel{\color{red}{x}} - \color{green}{1} + \cancel{\color{red}{x}}}}{{2\left( {1 + {x^2}} \right)}} } = { - \frac{1}{{1 + {x^2}}}.} \] Как видно, производная нигде не равна нулю. Поэтому других критических точек, кроме \(x = -1,\) у функции не существует. Следовательно, функция является монотонно убывающей (учитывая, что производная отрицательна всюду в области определения). В таком случае наибольшее и наименьшее значения функции достигаются на границах отрезка: \[ {f\left( 0 \right) = \arctan \frac{{1 - 0}}{{1 + 0}} = \arctan 1 = \frac{\pi }{4};}\;\;\; {f\left( 1 \right) = \arctan \frac{{1 - 1}}{{1 + 1}} = \arctan 0 = 0.} \] Наименьшее значение равно \(f\left( 1 \right) = 0,\) а наибольшее значение составляет \(f\left( 0 \right) = \large\frac{\pi }{4}\normalsize.\)

   Пример 10

\[f\left( x \right) = \left| {\sin x - \frac{{\sqrt 3 }}{2}} \right|,\;\;x \in \left[ {0,\pi } \right].\] Функция \(f\left( x \right)\) всюду неотрицательна. Ее наименьшее значение равно \(0\) и достигается на отрезке \(\left[ {0,\pi } \right]\) в следующих критических точках: \[ {\sin x - \frac{{\sqrt 3 }}{2} = 0,}\;\; {\Rightarrow \sin x = \frac{{\sqrt 3 }}{2},}\;\; {\Rightarrow {x_1} = \frac{\pi }{3},\;\;{x_2} = \frac{{2\pi }}{3}.} \] Чтобы определить наибольшее значение, вычислим производную данной функции: \[ {f'\left( x \right) = {\left( {\left| {\sin x - \frac{{\sqrt 3 }}{2}} \right|} \right)^\prime } } = {\frac{{\left| {\sin x - \frac{{\sqrt 3 }}{2}} \right|}}{{\sin x - \frac{{\sqrt 3 }}{2}}} \cdot {\left( {\sin x - \frac{{\sqrt 3 }}{2}} \right)^\prime } } = {\frac{{\left| {\sin x - \frac{{\sqrt 3 }}{2}} \right|}}{{\sin x - \frac{{\sqrt 3 }}{2}}} \cdot \cos x.} \] Критические точки \(x = \large\frac{\pi }{3}\normalsize,\) \(x = \large\frac{2\pi }{3}\normalsize,\) в которых выполняется равенство \({\sin x = \large\frac{{\sqrt 3 }}{2}}\normalsize,\) уже найдены выше. Поэтому рассмотрим лишь решение \[\cos x = 0,\;\; \Rightarrow x = \frac{\pi }{2}.\] Итак, наибольшее значение достигается либо в точке \(x = \large\frac{\pi }{2}\normalsize,\) либо на границах отрезка, т.е. в точках \(x = 0\) или \(x = \pi.\) Вычисления приводят к следующим результатам: \[ {f\left( {\frac{\pi }{2}} \right) = \left| {\sin \frac{\pi }{2} - \frac{{\sqrt 3 }}{2}} \right| } = {\left| {1 - \frac{{\sqrt 3 }}{2}} \right| \approx 0,732;} \] \[ {f\left( 0 \right) = \left| {\sin 0 - \frac{{\sqrt 3 }}{2}} \right| } = {\frac{{\sqrt 3 }}{2} \approx 1,732;} \] \[ {f\left( \pi \right) = \left| {\sin \pi - \frac{{\sqrt 3 }}{2}} \right| } = {\frac{{\sqrt 3 }}{2} \approx 1,732.} \] Таким образом, наибольшее значение равно \(\large\frac{{\sqrt 3 }}{2}\normalsize \approx 1,732\) и оно достигается в двух точках: \(x = 0,\) \(x = \pi.\)