Моделирование рекламной кампании

Дифференциальные уравнения широко используются для описания различных динамических процессов в экономике, логистике и маркетинге. Ниже мы рассмотрим как с помощью обыкновенных дифференциальных уравнений можно смоделировать рекламную кампанию.

Представим, что некоторая компания разработала новый продукт или сервис. Маркетинговая стратегия компании предполагает агрессивное рекламирование. Чтобы перейти к простой математической модели, введем две переменных:

• Величина \(q\left( t \right)\) представляет собой рекламную активность, которая описывается темпом расхода рекламного бюджета, например, суммой в рублях (или в любой другой валюте), которую компания тратит на рекламу за неделю;

• Величина \(A\left( t \right)\) описывает осведомленность целевой группы потенциальных покупателей нового товара или услуги.

Таким образом, мы рассматриваем рыночную нишу как черный ящик (рисунок \(1\)). Рекламная активность \(q\left( t \right)\) здесь играет роль входного параметра, а осведомленность потребителей \(A\left( t \right)\) является выходной переменной - она измеряет отклик системы на воздействие рекламы. Простая модель такого типа была предложена в \(1962\) году. Она называется моделью Нерлова-Эрроу (кратко \(N-A\) модель). Данная модель связывает между собой две введенные переменные: рекламную активность \(q\left( t \right)\) и осведомленность потребителей \(A\left( t \right)\) и описывается следующим дифференциальным уравнением: \[\frac{{dA}}{{dt}} = bq\left( t \right) - kA,\] где \(b\) − некоторая постоянная, описываюшая эффективность рекламы, \(k\) − константа, соответствующая скорости "забывания".

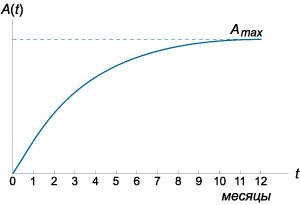
Данное уравнение содержит два члена в правой части. Первое слагаемое \(bq\left( t \right)\) обеспечивает линейный рост осведомленности потребителей в результате воздействия рекламы. Второй член \(-kA\) описывает противоположный процесс − забывание о рекламируемом продукте. Мы можем принять в первом приближении, что скорость забывания пропорциональна текущему уровню осведомленности \(A.\)

Полученное уравнение является линейным дифференциальным уравнением первого порядка. Его удобнее записать в стандартной форме: \[\frac{{dA}}{{dt}} + kA = bq\left( t \right).\] Интегрирующий множитель представляет собой экспоненциальную функцию: \[u\left( t \right) = {e^{\int {kdt} }} = {e^{kt}}.\] Следовательно, общее решение данного дифференциального уравнения выражается формулой \[A\left( t \right) = \frac{{b\int {{e^{kt}}q\left( t \right)dt} + C}}{{{e^{kt}}}}.\] Постоянную интегрирования \(C,\) как обычно, определяется из начального условия \(A\left( {{t_0}} \right) = {A_0}.\)

В приведенных ниже примерах мы исследуем как осведомленность потребителей \(A\left( t \right)\) зависит от режима рекламирования.

   Пример 1

Менеджмент компании принял решение о постоянном рекламировании нового продукта в течение года. Рекламный бюджет составляет \($12,000.\) Коэффициенты \(k\) и \(b\) равны: \(k = {\large\frac{1}{4}\normalsize},\;b = 25.\) Записать и решить дифференциальное уравнение, описывающее количество людей \(A\left( t \right),\) ознакомившихся с данным продуктом. Уравнение динамики \(A\left( t \right)\) записывается в виде: \[\frac{{dA}}{{dt}} + kA = bq\left( t \right).\] Будем считать, что время \(t\) измеряется в месяцах. По условию задачи, расходы на рекламу постоянны в течение всего года. Тогда ежемесячные рекламные расходы составляют: \[{q_0} = \frac{{12000}}{{12}} = 1000\,\frac{$}{\text{месяц}}.\] Подставляя известные значения, получаем следующее дифференциальное уравнение: \[\frac{{dA}}{{dt}} + \frac{A}{4} = 25000.\] В данном случае интегрирующий множитель имеет вид: \[u\left( t \right) = {e^{\int {{\large\frac{1}{4}\normalsize}dt} }} = {e^{\large\frac{t}{4}\normalsize}}.\] Следовательно, общее решение уравнения записывается в виде: \[ {A\left( t \right) = \frac{{25000\int {{e^{\large\frac{t}{4}\normalsize}}dt} + C}}{{{e^{\large\frac{t}{4}\normalsize}}}} } = {\frac{{\frac{{25000}}{{\frac{1}{4}}}{e^{\large\frac{t}{4}\normalsize}} + C}}{{{e^{\large\frac{t}{4}\normalsize}}}} } = {100000 + C{e^{ - \large\frac{t}{4}\normalsize}}.} \] Константу \(C\) определим из начального условия \(A\left( {t = 0} \right) = 0.\) Следовательно, \(C = -100000.\) В результате частное решение выражается формулой \[A\left( t \right) = 100000\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right).\] График этой функции показан выше на рисунке \(2,\) Таким образом, в случае постоянной рекламы число потенциальных покупателей растет нелинейно, приближаясь к максимальному значению \[{A_{\max }} = \frac{{b{q_0}}}{k} = 100000.\]

   Пример 2

Используя условия предыдущей задачи \(1,\) выяснить как изменится число потенциальных покупателей к концу года, если весь рекламный бюджет израсходовать равномерно в течение первых \(6\) месяцев? В данном случае режим рекламирования имеет ступенчатый характер. Схематически расходы на рекламу показаны ниже на рисунке \(3.\) Исследуем как изменится осведомленность потребителей \(A\left( t \right)\) по сравнению со случаем, рассмотренным в задаче \(1,\) когда рекламные расходы одинаковы в течение всего года.

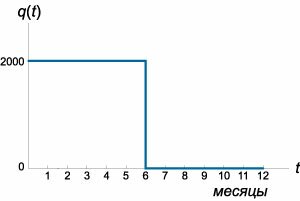
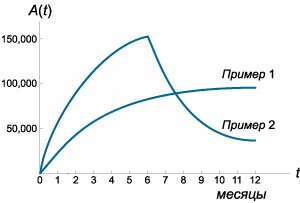
Задача разбивается на две стадии. К концу \(6\)-го месяца величина \(A\) легко вычисляется по формуле \[A\left( t \right) = \frac{{b{q_0}}}{k}\left( {1 - {e^{ - kt}}} \right),\] выведенной в примере \(1.\) Коэффициенты будут иметь следующие значения: \(k = \large\frac{1}{4}\normalsize,\) \(b = 25,\) \({q_0} = 2000.\) Тогда \[A\left( t \right) = 200000\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right).\] В момент \(t = 6\) количество покупателей, ознакомленных с продуктом, составляет: \[ {A\left( {t = 6} \right) } = {200000\left( {1 - {e^{ - \large\frac{6}{4}\normalsize}}} \right) } = {155374.} \] Во второй фазе − с \(7\)-го по \(12\)-й месяц включительно − реклама полностью отсутствует. В результате уровень осведомленности \(A\left( t \right)\) будет уменьшаться в соответствии с уравнением: \[\frac{{dA}}{{dt}} + kA = 0.\] Решение однородного уравнения определяется экспоненциальной функцией: \[A\left( t \right) = C{e^{ - k\left( {t - 6} \right)}},\] где \(t > 6\) месяцев. Константа \(C\) находится из начального условия для второй фазы: \[ {A\left( {t = 6} \right) = C{e^0} = C } = {155374 \approx 155400.} \] Таким образом, закон изменения \(A\left( t \right)\) во втором полугодии имеет вид: \[A\left( t \right) = 155400\,{e^{ - \large\frac{{t - 6}}{4}\normalsize}}.\] Итак, полное решение задачи записывается в виде: \[ A\left( {t} \right) = \begin{cases} 200000\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right), & 0 \le t \le 6 \\ 155400\,{e^{ - \large\frac{{t - 6}}{4}\normalsize}}, & 6 \lt t \le 12 \end{cases}. \] График функции \(A\left( t \right)\) представлен на рисунке \(4.\) На рисунке для сравнения показана также кривая \(A\left( t \right)\) из предыдущей задачи. Видно, что во втором случае осведомленность покупателей к концу года будет ниже, чем в режиме постоянного однородного рекламирования. Точные значения \(A\) для обоих случаев равны \[ {\text{Конец года:}}\;\;\; {A\left( {\text{пример}\,1} \right) = 95021;}\;\;\; {A\left( {\text{пример}\,2} \right) = 34669.} \] Интересно, что среднее значение \(A\) в течение года больше во втором случае: \[ {\text{Среднее значение:}}\;\;\; {\overline A\left( {\text{пример}\,1} \right) = 72117;}\;\;\; {\overline A\left( {\text{пример}\,2} \right) = 89825.} \] Можно грубо предположить, что объем продаж пропорционален осведомленности покупателей о новом продукте, так что режим ступенчатого рекламирования (при одинаковом рекламном бюджете!) является более выгодным с этой точки зрения.

   Пример 3

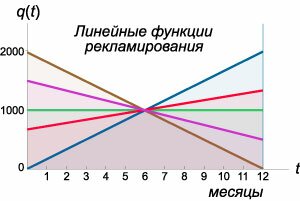
Исследовать динамику осведомленности \(A\left( t \right)\) для случая линейно изменяющейся рекламной активности \(q\left( t \right).\) Использовать те же данные, что и в примерах \(1,2.\) В данной задаче мы еще несколько усложним нашу маркетинговую модель. Будем предполагать, что рекламный бюджет расходуется в течение года по линейному закону: \[q\left( t \right) = {q_0} + \alpha t.\] Функция \(q\left( t \right)\) может быть как возрастающей, так и убывающей (рисунок \(5\)). В любом случае, общий годовой рекламный бюджет остается неизменным (Пусть он будет равен \(U\)). Графически это означает, что площади всех трапеций (или треугольников в предельном случае), показанных на рисунке \(6,\) равны.

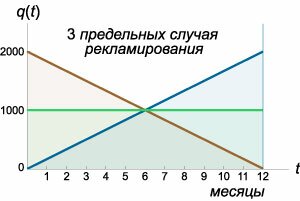
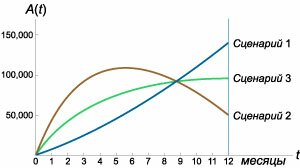
Ясно, что параметры \({q_0}\) и \(\alpha\) будут связаны следующим соотношением: \[12\left( {{q_0} + 6\alpha } \right) = U.\] Левая часть этой формулы соответствует площади трапеции. Поэтому коэффициент \(\alpha\) выражается через \({q_0}\) следующим образом: \[\alpha = \frac{1}{{72}}\left( {U - 12{q_0}} \right).\] Зависимость рекламных расходов от времени будет описываться формулой: \[q\left( t \right) = {q_0} + \frac{{\left( {U - 12{q_0}} \right)t}}{{72}}.\] Подставим последнее выражение в формулу общего решения \(A\left( t \right)\) и затем проинтегрируем: \[ {A\left( t \right) = \frac{{b\int {{e^{kt}}q\left( t \right)dt} + C}}{{{e^{kt}}}} } = {\frac{{b\int {{e^{kt}}\left( {{q_0} + \frac{{\left( {U - 12{q_0}} \right)t}}{{72}}} \right)dt} + C}}{{{e^{kt}}}} } = {\frac{{b{q_0}\int {{e^{kt}}dt} + \frac{{b\left( {U - 12{q_0}} \right)}}{{72}}\int {{e^{kt}}tdt} + C}}{{{e^{kt}}}}.} \] Интеграл \({\int {{e^{kt}}tdt} }\) в числителе можно найти, интегрируя по частям. Полагаем: \[ {u' = {e^{kt}},\;\;v = t,}\;\; {\Rightarrow u = \int {{e^{kt}}dt} = \frac{1}{k}{e^{kt}},\;\;v' = 1.} \] Следовательно, \[ {\int {{e^{kt}}tdt} = \frac{1}{k}{e^{kt}}t - \frac{1}{k}\int {{e^{kt}} \cdot 1dt} } = {\frac{1}{k}{e^{kt}}t - \frac{1}{{{k^2}}}{e^{kt}} } = {\frac{1}{k}{e^{kt}}\left( {t - \frac{1}{k}} \right).} \] В результате мы получаем следующее выражение для \(A\left( t \right):\) \[ {A\left( t \right) } = {\frac{{\frac{{b{q_0}}}{k}{e^{kt}} + \frac{{b\left( {U - 12{q_0}} \right)}}{{72}}\frac{1}{k}{e^{kt}}\left( {t - \frac{1}{k}} \right) + C}}{{{e^{kt}}}} } = {\frac{b}{k}\left[ {{q_0} + \frac{{U - 12{q_0}}}{{72}}\left( {t - \frac{1}{k}} \right)} \right] + C{e^{ - kt}}.} \] Константу \(C\) определим из начального условия \(A\left( {t = 0} \right) = 0:\) \[ {0 = \frac{b}{k}\left[ {{q_0} - \frac{{U - 12{q_0}}}{{72k}}} \right] + C,}\;\; {\Rightarrow C = - \frac{b}{k}\left[ {{q_0} - \frac{{U - 12{q_0}}}{{72k}}} \right].} \] Подставляя \(C\) в формулу для \(A\left( t \right),\) находим: \[ {A\left( t \right) } = {\frac{b}{k}\left[ {{q_0} - \frac{{U - 12{q_0}}}{{72k}} + \frac{{U - 12{q_0}}}{{72}}t} \right] } - {\frac{b}{k}\left[ {{q_0} - \frac{{U - 12{q_0}}}{{72k}}} \right]{e^{ - kt}} } = {\frac{b}{k}\left[ {{q_0} - \frac{{U - 12{q_0}}}{{72k}}} \right]\left( {1 - {e^{ - kt}}} \right) } + {\frac{{b\left( {U - 12{q_0}} \right)}}{{72k}}t.} \] Наконец, подставим известные величины: \(k = \large\frac{1}{4}\normalsize,\) \(b = 25,\) \(U = 12,000:\) \[ {A\left( t \right) } = {\frac{{25}}{{\frac{1}{4}}}\left[ {{q_0} - \frac{{12000 - 12{q_0}}}{{72 \cdot \frac{1}{4}}}} \right]\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right) } + {\frac{{25\left( {12000 - 12{q_0}} \right)}}{{72 \cdot \frac{1}{4}}}t } = {100\left[ {{q_0} - \frac{2}{3}\left( {1000 - {q_0}} \right)} \right]\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right) } + {100 \cdot \frac{{1000 - {q_0}}}{6}t.} \] Если положить \({q_0} = 1000\) (режим постоянного однородного рекламирования, рассмотренный в примере \(1\)), то мы получим уже найденную выше формулу: \[ {A\left( t \right) = 100 \cdot 1000\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right) + 0 } = {100,000\left( {1 - {e^{ - \large\frac{t}{4}\normalsize}}} \right).} \] Используя общее решение \(A\left( t \right),\) сравним динамику осведомленности для следующих предельных случаев: (смотрите рисунок \(6\) выше).

• Сценарий 1: Рекламные расходы линейно возрастают от 0 до 2000;

• Сценарий 2: Рекламные расходы линейно уменьшаются от 2000 до 0;

• Сценарий 3: Рекламные расходы постоянны в течение года.

Результаты расчетов представлены на рисунке \(7.\) Средние значения \(A\left( t \right)\) в течение года для указанных сценариев приведены в таблице (рисунок \(8\)). Как видно, наиболее агрессивный сценарий 2 может привести к росту продаж, хотя сценарий \(1\) имеет преимущество благодаря долговременному эффекту. Конечно, эти выводы ограничены точностью модели. В реальном бизнесе динамика \(A\left( t \right)\) может иметь более сложный характер.