Криволинейные интегралы второго рода

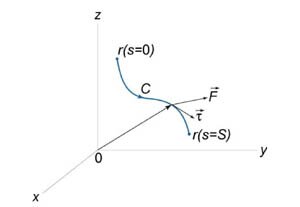
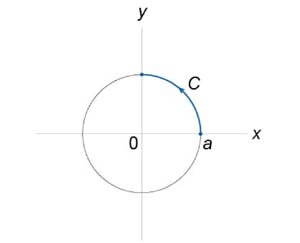
Предположим, что кривая \(C\) задана векторной функцией \(\mathbf{r} = \mathbf{r}\left( s \right),\) \(0 \le s \le S,\) где переменная \(s\) − длина дуги кривой. Тогда производная векторной функции \[ {\frac{{d\mathbf{r}}}{{dt}} = \boldsymbol{\tau} } = {\left( {\cos \alpha ,\cos \beta ,\cos \gamma } \right)} \] представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок \(1\)).

В приведенной выше формуле \(\alpha, \beta\) и \(\gamma\) − углы между касательной и положительными направлениями осей \(Ox, Oy\) и \(Oz,\) соответственно. Введем векторную функцию \(\mathbf{F}\left( {P,Q,R} \right),\) определенную на кривой \(C,\) так, чтобы для скалярной функции \[\mathbf{F} \cdot \boldsymbol{\tau} = P\cos \alpha + Q\cos \beta + R\cos \gamma \] существовал криволинейный интеграл \(\int\limits_C {\left( {\mathbf{F} \cdot \boldsymbol{\tau}} \right)ds} .\) Такой интеграл \(\int\limits_C {\left( {\mathbf{F} \cdot \boldsymbol{\tau}} \right)ds}\) называется криволинейным интегралом второго рода от векторной функции \(\mathbf{F}\) вдоль кривой \(C\) и обозначается как \[\int\limits_C {Pdx + Qdy + Rdz} .\] Таким образом, по определению, \[ {\int\limits_C {Pdx + Qdy + Rdz} } = {\int\limits_0^S {\left( {P\cos \alpha + Q\cos \beta + R\cos \gamma } \right)ds} ,} \] где \(\boldsymbol{\tau} \left( {\cos \alpha ,\cos \beta ,\cos \gamma } \right)\) − единичный вектор касательной к кривой \(C.\)

Последнюю формулу можно переписать также в векторной форме: \[ {\int\limits_C {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} } = {\int\limits_0^S {\left( {\mathbf{F}\left( {\mathbf{r}\left( s \right)} \right) \cdot \boldsymbol{\tau} } \right)ds} ,} \] где \(d\mathbf{r} = \left( {dx,dy,dz} \right).\)

Если кривая \(C\) лежит в плоскости \(Oxy,\) то полагая \(R = 0\) получаем \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_0^S {\left( {P\cos \alpha + Q\cos \beta } \right)ds} .} \]
Криволинейный интеграл \(II\) рода обладает следующими свойствами:

1. Пусть \(C\) обозначает кривую с началом в точке \(A\) и конечной точкой \(B.\) Обозначим через \(-C\) кривую противоположного направления − от \(B\) к \(A.\) Тогда \[\int\limits_{ - C} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} = - \int\limits_C {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} ;\]

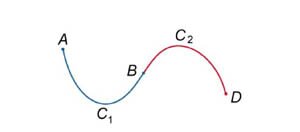
2. Если \(C\) − объединение кривых \({C_1}\) и \({C_2}\) (рисунок \(2\) выше), то \[ {\int\limits_C {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} } = {\int\limits_{{C_1} \cup {C_2}} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} } = {\int\limits_{{C_1}} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} + \int\limits_{{C_2}} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} ;} \]

3. Если кривая \(C\) задана параметрически в виде \(\mathbf{r}\left( t \right) = \left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right),\) \(\alpha \le t \le \beta ,\) то \[ {\int\limits_C {Pdx + Qdy + Rdz} } = {\int\limits_\alpha ^\beta {\left[ {P\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dx}}{{dt}} + Q\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dy}}{{dt}} + R\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dz}}{{dt}}} \right]dt} .} \]

4. Если кривая \(C\) лежит в плоскости \(Oxy\) и задана уравнением \(y = f\left( x \right)\) (предполагается, что \(R = 0\) и \(t = x\)), то последняя формула записывается в виде \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_a^b {\left[ {P\left( {x,f\left( x \right)} \right) + Q\left( {x,f\left( x \right)} \right)\frac{{df}}{{dx}}} \right]dx} .} \]

   Пример 1

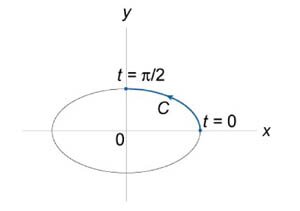
Вычислить интеграл \(\int\limits_C {ydx - xdy},\) где кривая \(C\) задана параметрически в виде \(\mathbf{r}\left( t \right) = \left( {\cos t,\sin t} \right),\;0 \le t \le \large\frac{\pi }{2}\normalsize.\) Используя формулу \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_\alpha ^\beta {\left[ {P\left( {x\left( t \right),y\left( t \right)} \right)\frac{{dx}}{{dt}} + Q\left( {x\left( t \right),y\left( t \right)} \right)\frac{{dy}}{{dt}}} \right]dt} ,} \] находим ответ: \[ {\int\limits_C {ydx - xdy} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {y\frac{{dx}}{{dt}} - x\frac{{dy}}{{dt}}} \right)dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\sin t\frac{{d\left( {\cos t} \right)}}{{dt}} - \cos t\frac{{d\left( {\sin t} \right)}}{{dt}}} \right)dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\sin t\left( { - \sin t} \right) - \cos t\cos t} \right)dt} } = { - \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {{{\sin }^2}t + {{\cos }^2}t} \right)dt} } = { - \int\limits_0^{\large\frac{\pi }{2}\normalsize} {dt} } = { - \frac{\pi }{2}.} \]

   Пример 2

Найти интеграл \(\int\limits_C {xdy - ydx} \) вдоль кривой \(C,\) заданной уравнением \(y = {x^3},\) от точки \(\left( {0,0} \right)\) до \(\left( {2,8} \right).\) Для вычисления данного криволинейного интеграла воспользуемся формулой \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_a^b {\left[ {P\left( {x,f\left( x \right)} \right) + Q\left( {x,f\left( x \right)} \right)\frac{{df}}{{dx}}} \right]dx} .} \] Подставляя \(y = {x^3}\) и \(dy = 3{x^2}dx\) в подынтегральное выражение, получаем \[ {\int\limits_C {xdy - ydx} } = {\int\limits_0^2 {x \cdot 3{x^2}dx - {x^3}dx} } = {\int\limits_0^2 {2{x^3}dx} } = {2\left[ {\left. {\left( {\frac{{{x^4}}}{4}} \right)} \right|_0^8} \right] = 8.} \]

   Пример 3

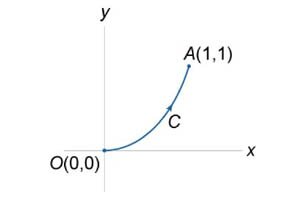
Вычислить \(\int\limits_C {\sqrt x dx + \sqrt y dy} \) вдоль кривой \(y = {x^2}\) от точки \(O\left( {0,0} \right)\) до \(A\left( {1,1} \right)\) (рисунок \(3\)). Используем формулу \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_a^b {\left[ {P\left( {x,f\left( x \right)} \right) + Q\left( {x,f\left( x \right)} \right)\frac{{df}}{{dx}}} \right]dx} .} \] Подставляя \(y = {x^2}\) и \(dy = 2xdx\) в подынтегральное выражение, находим ответ: \[ {\int\limits_C {\sqrt x dx + \sqrt y dy} } = {\int\limits_0^1 {\sqrt x dx + x \cdot 2xdx} } = {\int\limits_0^1 {\left( {{x^{\large\frac{1}{2}\normalsize}} + 2{x^2}} \right)dx} } = {\left. {\left( {\frac{{{x^{\large\frac{3}{2}\normalsize}}}}{{\frac{3}{2}}} + \frac{{2{x^3}}}{3}} \right)} \right|_0^1 } = {\frac{2}{3} + \frac{2}{3} = \frac{4}{3}.} \]

   Пример 4

Вычислить \(\int\limits_C {ydx + xdy} \) вдоль кривой \(y = {x^2}\) от точки \(O\left( {0,0} \right)\) до \(A\left( {1,1} \right)\) (рисунок \(3\)). Если \(y = f\left( x \right) = {x^2},\) то по формуле \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_a^b {\left[ {P\left( {x,f\left( x \right)} \right) + Q\left( {x,f\left( x \right)} \right)\frac{{df}}{{dx}}} \right]dx} .} \] получаем \[ {\int\limits_C {ydx + xdy} } = {\int\limits_0^1 {\left( {{x^2} + x \cdot 2x} \right)dx} } = {\int\limits_0^1 {3{x^2}dx} } = {3 \cdot \left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^1 = 1.} \]

   Пример 5

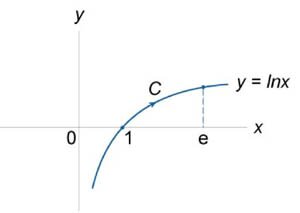
Вычислить криволинейный интеграл \(\int\limits_C {{\large\frac{y}{x}\normalsize} dx + dy} \) вдоль кривой \(y = \ln x\) в интервале \(1 \le x \le e\) (рисунок \(4\)). Поскольку \(y = \ln x,\) то дифференциал равен \(dy = \large\frac{{dx}}{x}\normalsize.\) В соответствии с формулой \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_a^b {\left[ {P\left( {x,f\left( x \right)} \right) + Q\left( {x,f\left( x \right)} \right)\frac{{df}}{{dx}}} \right]dx},} \] находим решение: \[ {\int\limits_C {\frac{y}{x}dx + dy} } = {\int\limits_1^e {\left( {\frac{{\ln x}}{x} + \frac{1}{x}} \right)dx} } = {\int\limits_1^e {\frac{{\ln x}}{x}dx} + \int\limits_1^e {\frac{{dx}}{x}} } = {\int\limits_1^e {\ln xd\left( {\ln x} \right)} + \int\limits_1^e {\frac{{dx}}{x}} } = {\left. {\left[ {\frac{{{{\left( {\ln x} \right)}^2}}}{2} + \ln x} \right]} \right|_1^e } = {\left( {\frac{{{{\left( {\ln e} \right)}^2}}}{2} + \ln e} \right) - \left( {\frac{{{{\left( {\ln 1} \right)}^2}}}{2} + \ln 1} \right) } = {\frac{1}{2} + 1 - 0 = \frac{3}{2}.} \]

   Пример 6

Вычислить криволинейный интеграл \(\int\limits_C {{x^2}dx - xydy},\) где \(C\) − дуга окружности, лежащая в первом квадранте, обход которой осуществляется против часовой стрелки (рисунок \(5\)). Очевидно, что дуга окружности описывается функцией \(y = \sqrt {{a^2} - {x^2}},\) \(a\) − радиус окружности. (Мы взяли положительное значение корня, поскольку \(y > 0\) в первом квадранте.) Тогда дифференциал равен \[ {dy = \frac{{dy}}{{dx}}dx } = {\frac{{d\sqrt {{a^2} - {x^2}} }}{{dx}}dx } = { - \frac{{xdx}}{{\sqrt {{a^2} - {x^2}} }}.} \] Поскольку мы обходим кривую в направлении против часовой стрелки, то нижний и верхний пределы интегрирования равны, соответственно, \(a\) и \(0.\) Следовательно, \[ {\int\limits_C {{x^2}dx - xydy} } = {\int\limits_a^0 {{x^2}dx - x\sqrt {{a^2} - {x^2}} \left( { - \frac{{xdx}}{{\sqrt {{a^2} - {x^2}} }}} \right)dx} } = {\int\limits_a^0 {2{x^2}dx} } = {2\left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_a^0} \right] } = { - \frac{{2{a^3}}}{3}.} \]

   Пример 7

Вычислить криволинейный интеграл \(\int\limits_C {{y^2}dx + xydy},\) где \(C\) − дуга эллипса (рисунок \(6\)), заданного параметрически в виде \(\mathbf{r}\left( t \right) = \left( {a\cos t,b\sin t} \right),\;0 \le t \le \large\frac{\pi }{2}\normalsize .\) Запишем все выражения через параметр \(t:\) \[ {{y^2} = {b^2}{\sin ^2}t,}\;\; {\frac{{dx}}{{dt}} = - a\sin t,}\;\; {xy = ab\cos t\sin t,}\;\; {\frac{{dy}}{{dt}} = b\cos t.} \] Далее, используя формулу \[ {\int\limits_C {Pdx + Qdy} } = {\int\limits_\alpha ^\beta {\left[ {P\left( {x\left( t \right),y\left( t \right)} \right)\frac{{dx}}{{dt}} + Q\left( {x\left( t \right),y\left( t \right)} \right)\frac{{dy}}{{dt}}} \right]dt} ,} \] можно записать \[ {\int\limits_C {{y^2}dx + xydy} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left[ {{b^2}{{\sin }^2}t \cdot \left( { - a\sin t} \right) + ab\cos t\sin t \cdot b\cos t} \right]dt} } = {\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left[ { - a{b^2}{{\sin }^3}t + a{b^2}{{\cos }^2}t\sin t} \right]dt} } = {a{b^2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left[ {\sin t\left( {{{\cos }^2}t - {{\sin }^2}t} \right)} \right]dt} } = {a{b^2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin t\cos 2tdt} } = {a{b^2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left[ {\frac{1}{2}\left( {\sin 3t + \sin \left( { - t} \right)} \right)} \right]dt} } = {\frac{{a{b^2}}}{2}\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {\sin 3t - \sin t} \right)dt} } = {\frac{{a{b^2}}}{2}\left[ {\left. {\left( { - \frac{{\cos 3t}}{3} + \cos t} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {\frac{{a{b^2}}}{2}\left[ {0 - \left( { - \frac{1}{3} + 1} \right)} \right] } = { - \frac{{a{b^2}}}{3}.} \]

   Пример 8

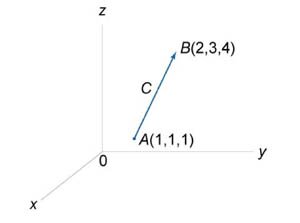
Найти интеграл \(\int\limits_C {xdx + ydy + \left( {x + y - 1} \right)dz} \) вдоль линии \(C,\) представляющей собой отрезок прямой от точки \(A\left( {1,1,1} \right)\) до точки \(B\left( {2,3,4} \right)\) (рисунок \(7\)). Сначала составим уравнение прямой \(AB:\) \[ {\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}},}\;\; {\Rightarrow \frac{{x - 1}}{{2 - 1}} = \frac{{y - 1}}{{3 - 1}} = \frac{{z - 1}}{{4 - 1}},}\;\; {\Rightarrow \frac{{x - 1}}{1} = \frac{{y - 1}}{2} = \frac{{z - 1}}{3}.} \] Введем параметр \(t:\) \[\frac{{x - 1}}{1} = \frac{{y - 1}}{2} = \frac{{z - 1}}{3} = t,\] и перепишем уравнение прямой в параметрической форме: \[ {\left\{ \begin{array}{l} x - 1 = t\\ y - 1 = 2t\\ z - 1 = 3t \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} x = t + 1\\ y = 2t + 1\\ z = 3t + 1 \end{array} \right..} \] Далее применяем формулу \[ {\int\limits_C {Pdx + Qdy + Rdz} } = {\int\limits_\alpha ^\beta {\left[ {P\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dx}}{{dt}} + Q\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dy}}{{dt}} + R\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dz}}{{dt}}} \right]dt} .} \] Очевидно, что параметр \(t\) изменяется в интервале \(\left[ {0,1} \right].\) Тогда криволинейный интеграл равен \[ {\int\limits_C {xdx + ydy + \left( {x + y - 1} \right)dz} } = {\int\limits_0^1 {\left[ {\left( {t + 1} \right)\frac{{d\left( {t + 1} \right)}}{{dt}} + \left( {2t + 1} \right)\frac{{d\left( {2t + 1} \right)}}{{dt}} + \left( {t + 1 + 2t + 1 - 1} \right)\frac{{d\left( {3t + 1} \right)}}{{dt}}} \right]dt} } = {\int\limits_0^1 {\left[ {t + 1 + \left( {2t + 1} \right) \cdot 2 + \left( {3t + 1} \right) \cdot 3} \right]dt} } = {\int\limits_0^1 {\left( {14t + 6} \right)dt} } = {\left. {\left( {7{t^2} + 6t} \right)} \right|_0^1 = 13.} \]