Кривизна плоских кривых

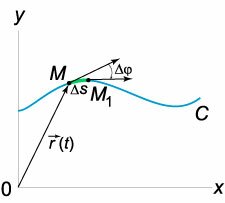
Пусть плоская кривая \(C\) задана параметрически радиус-вектором \(\mathbf{r}\left( t \right).\) При движении произвольной точки \(M\) вдоль кривой \(C\) ее касательная меняет направление (рисунок \(1\)). Кривизну кривой можно определить как отношение угла поворота касательной \(\Delta \varphi \) к длине пройденной дуги \(\Delta s = M{M_1}.\) Такое отношение \(\large\frac{{\Delta \varphi }}{{\Delta s}}\normalsize\) называется средней кривизной дуги кривой. Когда точка \({M_1}\) приближается к точке \(M,\) мы получаем кривизну кривой в точке \(M:\) \[k = \lim\limits_{\Delta s \to 0} \frac{{\Delta \varphi }}{{\Delta s}} = \frac{{d\varphi }}{{ds}}.\] Ясно, что кривизна \(k\) в общем случае может быть как положительной, так и отрицательной, в зависимости от направления вращения касательной.

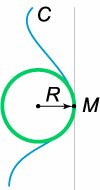
Если кривая задана своим радиусом вектором \(\mathbf{r}\left( t \right),\) ее кривизна определяется формулой \[k = \frac{{\mathbf{r'} \times \mathbf{r''}}}{{{{\left| {\mathbf{r'}} \right|}^3}}},\] где \(\mathbf{r}',\) \(\mathbf{r}''\) − первая и вторая производные радиус-вектора. В этой формуле в числителе записано векторное произведение векторов \(\mathbf{r}'\) и \(\mathbf{r}''.\)

При параметрическом задании координат кривой \(x\left( t \right)\) и \(y\left( t \right)\) формула для расчета кривизны принимает вид \[k = \frac{{x'y'' - y'x''}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}.\] Если плоская кривая задана явной функцией \(y = f\left( x \right),\) кривизна кривой вычисляется по формуле \[k = \frac{{y''}}{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}.\] В случае, когда кривая задана в полярных координатах в виде \(\rho = \rho \left( \varphi \right),\) ее кривизна \(k\) будет определяться выражением \[k\left( \varphi \right) = \frac{{{\rho ^2} + 2{{\left( {\rho '} \right)}^2} - \rho \rho ''}}{{{{\left[ {{\rho ^2} + {{\left( {\rho '} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}.\] Под кривизной кривой часто понимается абсолютное значение кривизны, без учета направления вращения касательной. В таком случае приведенные выше формулы остаются верными, но в числителе появляется модуль. Например, формула кривизны при параметрическом задании координат кривой \(x\left( t \right)\) и \(y\left( t \right)\) будет выглядеть так : \[k = \frac{{\left| {x'y'' - y'x'} \right|}}{{{{\left[ {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}\] Величина, обратная кривизне, называется радиусом кривизны: \[R = \frac{1}{{\left| k \right|}}.\] Окружность с таким радиусом и центром, расположенном на главной нормали, будет наилучшим образом аппроксимировать плоскую кривую в данной точке (рисунок \(2\)).

   Пример 1

Определить радиус кривизны прямой.
Пусть прямая задана явным уравнением \(y = ax + b,\) где \(a, b\) − некоторые коэффициенты. Вычислим кривизну \(k\) и радиус кривизны \(R\) данной прямой.

Абсолютное значение кривизны вычисляется по формуле \[k = \frac{{\left| {y''} \right|}}{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}.\] В нашем случае: \[y' = \left( {ax + b} \right) = a,\;\;y'' = a' = 0.\] Отсюда сразу следует, что кривизна прямой равна нулю, а радиус кривизны, соответственно, равен бесконечности.

   Пример 2

Определить уравнение переходной кривой железнодорожного пути. Как известно, при движении тела массой \(m\) со скоростью \(v\) вдоль кривой возникает центробежная сила, величина которой зависит от радиуса кривизны \(R:\) \[F = \frac{{m{v^2}}}{R}.\] Центробежная сил будет оставаться постоянной в случае, когда тело (например, поезд) движется по дуге окружности. Чтобы исключить резкие толчки при переходе от прямолинейного движения к круговому, используют специальные переходные участки, где кривизна постепенно и равномерно нарастает от \(0\) до конечного значения \(\large\frac{1}{R}\normalsize.\) На таких переходных кривых центробежная сила также будет изменяться равномерно.

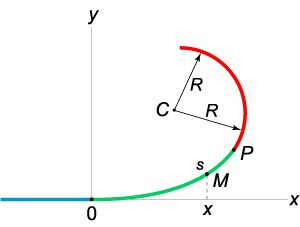
Пусть переходная кривая соответствует дуге \(OP\) (рисунок \(3\)), длина которой равна \(L.\) При движении точки \(M\) вдоль этой кривой радиус кривизны изменяется пропорционально пройденному пути \(s:\) \[\frac{1}{r} = ms,\] где \(m\) − коэффициент пропорциональности. Данный коэффициент легко найти из граничного условия: при \(s = OP = L\) кривизна станет равной \(\large\frac{1}{R}\normalsize:\) \[\frac{1}{R} = mL,\;\; \Rightarrow m = \frac{1}{{LR}}.\] Тогда условие для переходной кривой можно записать в виде следующего уравнения: \[ {k = \frac{1}{r} = \frac{s}{{LR}},}\;\; {\Rightarrow \frac{{y''}}{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}} = \frac{s}{{LR}}.} \] Решение задачи упрощается, если приблизительно положить \(s = x,\) где \(x\) − проекция точки \(M\) на ось \(Ox.\) При этом производная \(y'\) также будет мала и мы можем пренебречь ей в формуле для расчета кривизны. В результате получаем следующее дифференциальное уравнение переходной кривой: \[y'' = \frac{x}{{LR}}.\] Дважды интегрируя, находим общее решение уравнения: \[ {y' = \frac{{{x^2}}}{{2LR}} + {C_1},}\;\; {y = \frac{{{x^3}}}{{6LR}} + {C_1}x + {C_2}.} \] Учитывая начальные условия \(y\left( {x = 0} \right) = 0\) и \(y'\left( {x = 0} \right) = 0,\) получаем окончательное уравнение переходной кривой: \[y = \frac{{{x^3}}}{{6LR}},\] которая, как видно, является кубической параболой.

   Пример 3

Найти кривую, у которой радиус кривизны является постоянной величиной.
Пусть кривая задана уравнением \(y = y\left( x \right).\) Ее радиус кривизны определяется формулой \[R = \frac{1}{{\left| k \right|}} = \frac{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}}{{\left| {y''} \right|}}.\] Поскольку по условию задачи радиус является постоянной величиной \(R = \text{const},\) получаем следующее дифференциальное уравнение: \[\frac{{\left| {y''} \right|}}{{{{\left[ {1 + {{\left( {y'} \right)}^2}} \right]}^{\large\frac{3}{2}\normalsize}}}} = \frac{1}{R}.\] Сделаем замену \(y' = p\) и понизим порядок уравнения: \[\frac{{\left| {p'} \right|}}{{{{\left[ {1 + {p^2}} \right]}^{\large\frac{3}{2}\normalsize}}}} = \frac{1}{R}.\] Разделяя переменные и раскрывая модуль, получаем \[\int {\frac{{dp}}{{{{\left( {1 + {p^2}} \right)}^{\large\frac{3}{2}\normalsize}}}}} = \pm \int {\frac{{dx}}{R}} .\] Применим еще одну подстановку: \[ {p = \tan z,}\;\; {\Rightarrow z = \arctan p,}\;\; {dz = \frac{{dp}}{{1 + {p^2}}}.} \] Следовательно, уравнение принимает вид \[\int {\frac{{dz}}{{\sqrt {1 + {{\tan }^2}z} }}} = \pm \int {\frac{{dx}}{R}} .\] Вспоминая тригонометрическое тождество \[1 + {\tan ^2}z = \frac{1}{{{{\cos }^2}z}},\] данное уравнение можно упростить и затем проинтегрировать: \[ {\int {\cos zdz} = \pm \int {\frac{{dx}}{R}} ,}\;\; {\Rightarrow \sin z = \pm \frac{1}{R}\left( {x + {C_1}} \right),} \] где \({C_1}\) − постоянная интегрирования.

Перейдем обратно к переменной \(p,\) учитывая соотношение \[\sin z = \sqrt {\frac{{{{\tan }^2}z}}{{{{\tan }^2}z + 1}}} .\] Здесь мы рассматриваем лишь положительное значение квадратного корня, поскольку оба знака уже фигурируют в правой части дифференциального уравнения. Тогда уравнение записывается в виде \[ {{\left[ {\frac{{{{\tan }^2}\left( {\arctan p} \right)}}{{{{\tan }^2}\left( {\arctan p} \right) + 1}}} \right]^{\large\frac{1}{2}\normalsize}} = \pm \frac{1}{R}\left( {x + {C_1}} \right),}\;\; {\Rightarrow \frac{{{p^2}}}{{{p^2} + 1}} = \frac{1}{{{R^2}}}{\left( {x + {C_1}} \right)^2}.} \] Вернемся к исходной переменной \(y:\) \[ {\frac{{{{\left( {y'} \right)}^2}}}{{{{\left( {y'} \right)}^2} + 1}} = \frac{1}{{{R^2}}}{\left( {x + {C_1}} \right)^2},}\;\; {\Rightarrow {\left( {y'} \right)^2} = \frac{1}{{{R^2}}}{\left( {x + {C_1}} \right)^2}\left( {{{\left( {y'} \right)}^2} + 1} \right),}\;\; {\Rightarrow {\left( {y'} \right)^2}\left[ {{R^2} - {{\left( {x + {C_1}} \right)}^2}} \right] = {\left( {x + {C_1}} \right)^2},}\;\; {\Rightarrow {\left( {y'} \right)^2} = \frac{{{{\left( {x + {C_1}} \right)}^2}}}{{{R^2} - {{\left( {x + {C_1}} \right)}^2}}},}\;\; {\Rightarrow y' = \pm \sqrt {\frac{{{{\left( {x + {C_1}} \right)}^2}}}{{{R^2} - {{\left( {x + {C_1}} \right)}^2}}}} ,}\;\; {\Rightarrow y = \pm \int {\sqrt {\frac{{{{\left( {x + {C_1}} \right)}^2}}}{{{R^2} - {{\left( {x + {C_1}} \right)}^2}}}} dx} .} \] Чтобы вычислить полученный интеграл сделаем замену переменной (надеемся, что она будет последней в этой задаче): \[x + {C_1} = R\sin t,\;\; \Rightarrow dx = R\cos tdt.\] Интеграл будет равен \[ {y = \pm \int {\sqrt {\frac{{{{\left( {x + {C_1}} \right)}^2}}}{{{R^2} - {{\left( {x + {C_1}} \right)}^2}}}} dx} } = { \pm \int {\sqrt {\frac{{{R^2}\,{{\sin }^2}t}}{{{R^2} - {R^2}\,{{\sin }^2}t}}} R\cos tdt} } = { \pm R\int {\tan t\cos tdt} } = { \pm R\int {\sin t dt} } = { \mp R\cos t + {C_2}.} \] Полученное выражение перепишем как \[y + {C_2} = \pm R\cos t.\] Исключим промежуточную переменную \(t:\) \[ {{\sin ^2}t + {\cos ^2}t = 1,}\;\; {\Rightarrow \frac{1}{{{R^2}}}{\left( {x + {C_1}} \right)^2} + \frac{1}{{{R^2}}}{\left( {y + {C_2}} \right)^2} = 1,}\;\; {\Rightarrow {\left( {x + {C_1}} \right)^2} + {\left( {y + {C_2}} \right)^2} = {R^2}.} \] Отсюда видно, что кривые с постоянным радиусом кривизны \(R\) представляют собой множество окружностей с произвольным центром и таким же радиусом \(R.\)