Кривая обучения

Освоение новой темы и приобретение новых навыков всегда требует времени. В данном разделе мы попробуем смоделировать процесс обучения, используя дифференциальные уравнения.

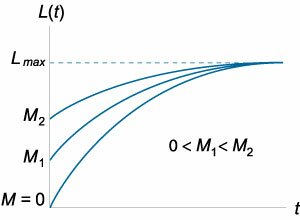
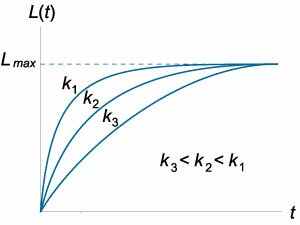
Прежде всего, введем некоторую измеряемую функцию обучения \(L\left( t \right).\) Эта функция может описывать, например, текущую производительность труда работника. Пусть \({L_{\max }}\) будет являться максимально возможным значением \(L\left( t \right).\) Во многих случая справедливо следующее эмпирическое правило: скорость обучения пропорциональна объему оставшегося (еще невыученного) материала. Математически это представляется уравнением вида \[\frac{{dL}}{{dt}} = k\left( {{L_{\max }} - L} \right),\] где \(k\) − коэффициент пропорциональности. Данное дифференциальное уравнение является уравнением с разделяющимися переменными, и его легко можно решить в общем виде: \[ {\frac{{dL}}{{dt}} = k\left( {{L_{\max }} - L} \right),}\;\; {\Rightarrow \frac{{dL}}{{{L_{\max }} - L}} = kdt,}\;\; {\Rightarrow \int {\frac{{dL}}{{{L_{\max }} - L}}} = \int {kdt} ,}\;\; {\Rightarrow - \int {\frac{{d\left( {{L_{\max }} - L} \right)}}{{{L_{\max }} - L}}} = \int {kdt} ,}\;\; {\Rightarrow - \ln \left( {{L_{\max }} - L} \right) = kt + \ln C,}\;\; {\Rightarrow \ln \left( {{L_{\max }} - L} \right) = - kt + \ln C,}\;\; {\Rightarrow \ln \left( {{L_{\max }} - L} \right) = \ln {e^{ - kt}} + \ln C.} \] Избавляясь от логарифмов, получаем общее решение в форме: \[{L_{\max }} - L = C{e^{ - kt}}.\] Постоянную \(C\) можно определить из начального условия: \(L\left( {t = 0} \right) = M.\) Следовательно, \(C = {L_{\max }} - M.\) В результате кривая обучения описывается формулой \[L\left( t \right) = {L_{\max }} - \left( {{L_{\max }} - M} \right){e^{ - kt}}.\] В последнем выражении параметр \(M\) означает начальный уровень знаний или навыков. В простейшем случае можно предположить, что \(M = 0.\) Другой параметр \(k\) "контролирует" скорость обучения. Вид кривых обучения при различных значениях \(M\) и \(k\) показан на рисунках \(1\) и \(2,\) соответственно. Как видно, кривая обучения \(L\) во всех случаях быстрее возрастает в начале процесса, а затем по мере снижения скорости обучения кривая приближается к максимальному значению \({L_{\max }}.\)

   Пример 1

Фармацевт в некоторой аптеке должен проверять \(1000\) рецептов в день. Новый фармацевт после найма на работу через \(1\) неделю смог проверить \(100\) рецептов в день. Оценить число рецептов, которые фармацевт сможет проверить в течение дня еще через одну неделю. Для простоты положим начальный уровень навыка равным нулю: \(M = 0.\) Процесс обучения можно описать следующим законом: \[L\left( t \right) = {L_{\max }}\left( {1 - {e^{ - kt}}} \right).\] Определим параметр \(k,\) зная количество рецептов, которые проверяются через \(1\) неделю: \[ {100 = 1000\left( {1 - {e^{ - kt}}} \right),}\;\; {\Rightarrow 1 - {e^{ - kt}} = 0.1,}\;\; {\Rightarrow {e^{ - kt}} = 0.9,}\;\; {\Rightarrow - kt = \ln 0.9,}\;\; {\Rightarrow k = - \frac{{\ln 0.9}}{t}.} \] Подставляя \(t = 1\,\text{неделя},\) находим: \[k = - \frac{{\ln 0.9}}{1} \approx - 0.105\] Теперь можно вычислить производительность нового фармацевта спустя две недели после начала работы: \[ {L\left( {t = 2} \right) = 1000\left( {1 - {e^{ - 0.105 \cdot 2}}} \right) } = {1000\left( {1 - {e^{ - 0.21}}} \right) } \approx {1000\left( {1 - 0.811} \right) } = {189\left[ {\frac{\text{рецептов}}{\text{день}}} \right].} \]

   Пример 2

Предположим, что новость распространяется в средствах массовой информации по закону, описываемому кривой обучения. Каков должен быть первоначальный процент "популяции", осведомленных об этой новости, так чтобы через \(1\) неделю это уровень достигнул \(50\%,\) а через \(4\) недели − \(90\%?\) Новость распространяется по закону: \[L\left( t \right) = {L_{\max }} - M{e^{ - kt}}.\] Мы знаем две точки на этой кривой: в моменты времени \(t = 1\,\text{неделя}\) и \(t = 4\,\text{недели}.\) Поэтому, можно записать следующие два уравнения: \[\left\{ \begin{array}{l} L\left( {t = 1} \right) = 0.5{L_{\max }} = {L_{\max }} - r{L_{\max }}{e^{ - k \cdot 1}}\\ L\left( {t = 4} \right) = 0.9{L_{\max }} = {L_{\max }} - r{L_{\max }}{e^{ - k \cdot 4}} \end{array} \right..\] Здесь параметр \(M\) представлен как \(r{L_{\max }},\) где \(r\) лежит в интервале \(0 \le r \le 1,\) а время \(t\) выражено в неделях.

Разделив на \({L_{\max }},\) получаем систему уравнений с двумя неизвестными: \(r\) и \(k:\) \[\left\{ \begin{array}{l} 0.5 = 1 - r{e^{ - k}}\\ 0.9 = 1 - r{e^{ - 4k}} \end{array} \right.,\;\; \Rightarrow \left\{ \begin{array}{l} r{e^{ - k}} = 0.5\\ r{e^{ - 4k}} = 0.1 \end{array} \right..\] Возьмем логарифмы от обеих частей каждого уравнения: \[\left\{ \begin{array}{l} \ln r - k = \ln 0.5\\ \ln r - 4k = \ln 0.1 \end{array} \right..\] Исключим параметр \(k\) из системы, умножая первое уравнение на \(\left( { - 4} \right)\) и затем складывая оба уравнения: \[ {\left. {\left\{ \begin{array}{l} - 4\ln r + 4k = - 4\ln 0.5\\ \ln r - 4k = \ln 0.1 \end{array} \right.} \right| + ,}\;\; {\Rightarrow - 3\ln r = \ln 0.1 - 4\ln 0.5,}\;\; {\Rightarrow \ln r = \frac{1}{3}\left( {4\ln 0.5 - \ln 0.1} \right).} \] В результате простых вычислений получаем ответ: \[ {\ln r = \frac{1}{3}\left( {4\ln 0.5 - \ln 0.1} \right) } \approx {\frac{1}{3}\left[ {4 \cdot \left( { - 0.693} \right) - \left( { - 2.302} \right)} \right] } = {\frac{1}{3}\left( { - 0.469} \right) } = { - 0.156} \] Отсюда следует, что параметр \(r\) равен \[r = {e^{ - 0.156}} \approx 0.855\] Таким образом, в данном случае начальный уровень "проникновения" новости должен составлять \[ {L\left( {t = 0} \right) = {L_{\max }} - r{L_{\max }} } = {{L_{\max }} - 0.855{L_{\max }} } = {0.145{L_{\max }} } \approx {15\% {L_{\max }}.} \]