Колебания в электрических цепях

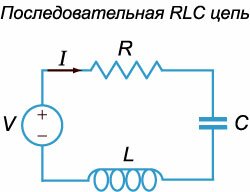
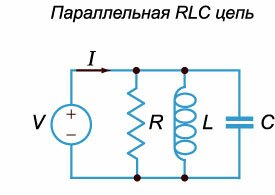
В электрической цепи, содержащей сопротивление \(R\), индуктивность \(L\) и емкость \(C\), могут возбуждаться электрические колебания. С точки зрения топологии чаще всего рассматриваются два вида электрических цепей: последовательная \(RLC\)-цепь (рисунок \(1\)) и параллельная \(RLC\)-цепь (рисунок \(2\)). Выведем дифференциальное уравнение, описывающее закон изменения тока в последовательной \(RLC\)-цепи.

Напряжения \({V_R},{V_C},{V_L},\) соответственно, на резисторе \(R,\) конденсаторе \(C\) и катушке индуктивности \(L\) выражаются формулами \[ {{V_R}\left( t \right) = RI\left( t \right),}\;\; {{V_C}\left( t \right) = \frac{1}{C}\int\limits_0^t {I\left( \tau \right)d\tau } ,}\;\; {{V_L}\left( t \right) = L\frac{{dI}}{{dt}}.} \] Из второго закона Кирхгофа следует, что \[{V_R}\left( t \right) + {V_C}\left( t \right) + {V_L}\left( t \right) = E\left( t \right),\] где \(E\left( t \right)\) − электродвижущая сила (э.д.с.) источника питания.

В случае постоянной э.д.с. \(E\) после подстановки выражений для \({V_R},{V_C}\) и \({V_L},\) и последующего дифференцирования получаем следующее дифференциальное уравнение: \[\frac{{{d^2}I\left( t \right)}}{{d{t^2}}} + \frac{R}{L}\frac{{dI\left( t \right)}}{{dt}} + \frac{1}{{LC}}I\left( t \right) = 0.\] Если ввести обозначения \(2\beta = {\large\frac{R}{L}\normalsize},\;\omega _0^2 = {\large\frac{1}{{LC}}\normalsize},\) то уравнение записывается в виде \[\frac{{{d^2}I}}{{d{t^2}}} + 2\beta \frac{{dI}}{{dt}} + \omega _0^2I = 0.\] Данное дифференциальное уравнение совпадает с уравнением, описывающим затухающие колебания грузика на пружинке. Следовательно, в последовательной \(RLC\)-цепи при определенных значениях параметров также могут возникать затухающие колебания.

Теперь рассмотрим параллельную \(RLC\)-цепь и выведем для нее аналогичное дифференциальное уравнение.

По первому закону Кирхгофа полный ток будет равен сумме токов через сопротивление \(R,\) катушку индуктивности \(L\) и конденсатор \(C\) (рисунок \(2\)): \[{I_R}\left( t \right) + {I_L}\left( t \right) + {I_C}\left( t \right) = I\left( t \right).\] Учитывая, что \[ {{I_R} = \frac{V}{R},}\;\;\; {{I_L} = \frac{1}{L}\int\limits_0^t {Vd\tau } ,}\;\;\; {{I_C} = C\frac{{dV}}{{dt}},} \] для случая постоянного полного тока \(I\left( t \right) = {I_0}\) получаем следующее дифференциальное уравнение \(2\)-го порядка относительно переменной \(V:\) \[ {\frac{V}{R} + \frac{1}{L}\int\limits_0^t {Vd\tau } + C\frac{{dV}}{{dt}} = {I_0},}\;\; {\Rightarrow C\frac{{{d^2}V}}{{d{t^2}}} + \frac{1}{R}\frac{{dV}}{{dt}} + \frac{1}{L}V = 0.} \] Как видно, мы снова приходим к уравнению, описывающему затухающие колебания. Таким образом, колебательный режим может возникать и в параллельных \(RLC\)-цепях. В простейшем случае, когда омическое сопротивление равно нулю (\(R = 0\)) и источник э.д.с. отсутствует (\(E = 0\)), колебательный контур состоит лишь из конденсатора \(C\) и катушки индуктивности \(L\) и описывается дифференциальным уравнением \[\frac{{{d^2}I}}{{d{t^2}}} + \omega _0^2I = 0,\;\; \text{где}\;\;\omega _0^2 = \frac{1}{{LC}}.\] В таком контуре будут происходить незатухающие электрические колебания с периодом \[{T_0} = \frac{{2\pi }}{{{\omega _0}}} = 2\pi \sqrt {LC} .\] Данная формула называется формулой Томсона в честь английского физика Уильяма Томсона (\(1824-1907\)), который теоретически вывел ее в \(1853\) году. Выше мы получили дифференциальное уравнение второго порядка, описывающее затухающие колебания в последовательном \(RLC\)-контуре, которое записывается как \[\frac{{{d^2}I}}{{d{t^2}}} + \frac{R}{L}\frac{{dI}}{{dt}} + \frac{1}{{LC}}I = 0.\] Соответствующее характеристическое уравнение имеет вид \[{\lambda ^2} + \frac{R}{L}\lambda + \frac{1}{{LC}} = 0.\] Его корни вычисляются по формулам: \[ {{\lambda _{1,2}} = \frac{{ - \frac{R}{L} \pm \sqrt {\frac{{{R^2}}}{{{L^2}}} - \frac{4}{{LC}}} }}{2} } = { - \frac{R}{{2L}} \pm \sqrt {{{\left( {\frac{R}{{2L}}} \right)}^2} - \frac{1}{{LC}}} } = { - \beta \pm \sqrt {{\beta ^2} - \omega _0^2} ,} \] где величина \(\beta = \large\frac{R}{{2L}}\normalsize\) называется коэффициентом затухания, а \({\omega_0}\) − резонансной частотой колебательного контура.

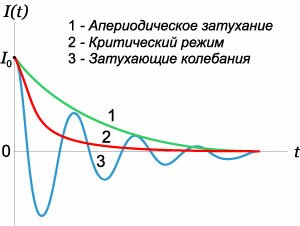
В зависимости от значений параметров \(R, L, C\) могут возникнуть три режима. В этом случае оба корня характеристического уравнения \({\lambda_1}\) и \({\lambda_2}\) действительны, различны и отрицательны. Общее решение дифференциального уравнения определяется формулой \[I\left( t \right) = {C_1}{e^{{\lambda _1}t}} + {C_2}{e^{{\lambda _2}t}}.\] В этом режиме ток монотонно уменьшается, приближаясь к нулю (рисунок \(3\)). Данный режим можно назвать граничным или критическим. Здесь оба корня характеристического уравнения совпадают, но при этом являются действительными и отрицательными. Общее решение уравнения выражается функцией \[ {I\left( t \right) = \left( {{C_1}t + {C_2}} \right){e^{ - \beta t}} } = {\left( {{C_1}t + {C_2}} \right){e^{ - {\large\frac{R}{{2L}}\normalsize} t}}.} \] В начале процесса ток может даже возрастать, но в дальнейшем он быстро уменьшается по экспоненциальному закону. В этом случае корни характеристического уравнения являются комплексно-сопряженными. В электрической цепи возникают затухающие колебания. Закон изменения тока имеет вид \[I\left( t \right) = {e^{ - \beta t}}\left( {A\cos \omega t + B\sin \omega t} \right),\] где величина \(\beta = \large\frac{R}{{2L}}\normalsize\) − как и выше, коэффициент затухания, \(\omega = \sqrt {{\large\frac{1}{{LC}}\normalsize} - {{\left( {\large\frac{R}{{2L}}\normalsize} \right)}^2}} \) − частота колебаний, \(A, B\) − постоянные интегрирования, зависящие от начальных условий. Заметим, что частота затухающих колебаний \(\omega\) меньше резонансной частоты \({\omega_0}\) колебательного контура. 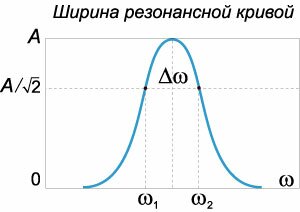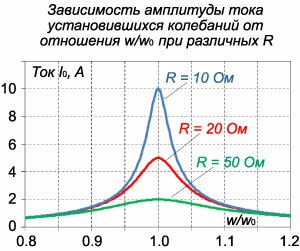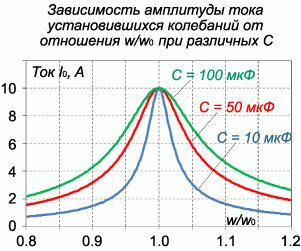Типичный вид кривой \(I\left( t \right)\) в этом режиме также представлен на рисунке \(3.\) Если колебательный контур содержит генератор с периодически изменяющейся э.д.с., то в нем устанавливаются вынужденные колебания. Если э.д.с. \(E\) источника тока изменяется по закону \[E\left( t \right) = {E_0}\cos \omega t,\] то дифференциальное уравнение вынужденных колебаний в последовательной \(RLC\)-цепи записывается в виде \[ {\frac{{{d^2}q\left( t \right)}}{{d{t^2}}} + \frac{R}{L}\frac{{dq\left( t \right)}}{{dt}} + \frac{1}{{LC}}q\left( t \right) = \frac{1}{L}{E_0}\cos \omega t}\;\; {\text{или}\;\;\frac{{{d^2}q}}{{d{t^2}}} + 2\beta \frac{{dq}}{{dt}} + \omega _0^2q = \frac{{{E_0}}}{L}\cos \omega t,} \] где \(q\) − заряд конденсатора, \(2\beta = \frac{R}{L},\;\omega _0^2 = \frac{1}{{LC}}.\)

Данное уравнение аналогично уравнению вынужденных колебаний пружинного маятника, рассмотренного на странице Механические колебания. Его общее решение представляет собой сумму двух слагаемых − общего решения однородного уравнения и частного решения неоднородного уравнения. При этом общее решение однородного уравнения описывает затухающий переходный процесс, по истечении которого в системе устанавливаются вынужденные колебания. Эти вынужденные колебания будут происходить по закону \[ {q\left( t \right) } = {\frac{{{E_0}}}{{L\sqrt {{{\left( {\omega _0^2 - {\omega ^2}} \right)}^2} + 4{\beta ^2}{\omega ^2}} }}\cos \left( {\omega t + \varphi } \right) } = {\frac{{{E_0}}}{{\omega \sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}\cos \left( {\omega t + \varphi } \right),} \] где фаза \(\varphi\) определяется формулой \[ {\varphi = \arctan \left( { - \frac{{2\beta \omega }}{{\omega _0^2 - {\omega ^2}}}} \right) } = {\arctan \frac{R}{{\omega L - \frac{1}{{\omega C}}}}.} \] Зная закон изменения заряда \(q\left( t \right),\) легко найти закон изменения тока \(I\left( t \right):\) \[ {I\left( t \right) = \frac{{dq\left( t \right)}}{{dt}} } = { - \frac{{{E_0}}}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}\sin\left( {\omega t + \varphi } \right) } = {\frac{{{E_0}}}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}\cos\left( {\omega t - \theta } \right),} \] где введен угол \(\theta,\) равный \(\theta = - \left( {\varphi + \frac{\pi }{2}} \right).\) Угол \(\theta\) показывает отставание колебаний тока \(I\left( t \right)\) по отношению к колебаниям напряжения источника питания \(E\left( t \right) = {E_0}\cos \omega t.\)

Амплитуда тока \({I_0}\) и сдвиг фаз \(\theta\) определяются формулами \[ {{I_0} = \frac{{{E_0}}}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }} = \frac{{{E_0}}}{Z},}\;\;\; {\theta = \arctan \frac{{\omega L - \frac{1}{{\omega C}}}}{R}.} \] Величина \(Z = \sqrt {{R^2} + {{\left( {\omega L - \large\frac{1}{{\omega C}}\normalsize} \right)}^2}} \) называется полным сопротивлением или импедансом контура. Она состоит из омического сопротивления \(R\) и реактивного сопротивления \({\omega L - \large\frac{1}{{\omega C}}}\normalsize\) Импеданс колебательного контура в комплексной форме записывается как \[Z = R + i\left( {\omega L - \frac{1}{{\omega C}}} \right).\] Из полученных формул видно, что амплитуда установившихся колебаний тока будет максимальной когда \[\omega L = \frac{1}{{\omega C}}\;\;\text{или}\;\;\omega = {\omega _0} = \frac{1}{{\sqrt {LC} }}.\] При этом условии в колебательном контуре наступает резонанс. Резонансная частота \({\omega_0}\) равна частоте свободных колебаний в контуре и не зависит от сопротивления \(R.\)

Формулу для амплитуды тока вынужденных колебаний можно преобразовать, выделив в явном виде зависимость от отношения частот \(\large\frac{\omega }{{{\omega _0}}}\normalsize,\) где \({\omega_0}\) − резонансная частота. В результате получаем \[\require{cancel} {{I_0} = \frac{{{E_0}}}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }} } = {\frac{{\frac{{{E_0}}}{{{\omega _0}}}}}{{\frac{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}{{{\omega _0}}}}} } = {\frac{{\frac{{{E_0}}}{{{\omega _0}}}}}{{\sqrt {\frac{{{R^2}}}{{\omega _0^2}} + {{\left( {\frac{\omega }{{{\omega _0}}}L - \frac{1}{{\omega {\omega _0}C}}} \right)}^2}} }} } = {\frac{{{E_0}\sqrt {LC} }}{{\sqrt {{R^2}LC + {{\left( {\frac{\omega }{{{\omega _0}}}L - \frac{1}{{\frac{\omega }{{{\omega _0}}}\frac{\cancel{C}}{{L\cancel{C}}}}}} \right)}^2}} }} } = {\frac{{{E_0}\sqrt {LC} }}{{\sqrt {{R^2}LC + {{\left( {\frac{\omega }{{{\omega _0}}}L - \frac{L}{{\frac{\omega }{{{\omega _0}}}}}} \right)}^2}} }} } = {\frac{{{E_0}\sqrt C }}{{\sqrt {{R^2}C + {{\left( {\frac{\omega }{{{\omega _0}}} - \frac{1}{{\frac{\omega }{{{\omega _0}}}}}} \right)}^2}} }}.} \] Типичные зависимости амплитуды тока от отношения частот \(\large\frac{\omega }{{{\omega _0}}}\normalsize\) при различных значениях \(R\) и \(C\) показаны на рисунках \(5\) и \(6.\) Данные графики построены при \(E = 100\;\text{В},\) \(L = 1\;\text{мГн},\) \(C = 10\;\text{мкФ}\) (на рисунке \(5\)), \(R = 10\;\text{Ом}\) (на рисунке \(6\)). Резонансные свойства колебательного контура характеризуются добротностью \(Q,\) которая численно равна отношению резонансной частоты \({\omega_0}\) к ширине резонансной кривой \(\Delta\omega\) на уровне убывания амплитуды в \(\sqrt 2\) раз (см. выше рисунок \(4\)).

В последовательном колебательном контуре добротность вычисляется по формуле \[Q = \frac{1}{R}\sqrt {\frac{L}{C}} .\] Для параллельной \(RLC\)-цепи добротность определяется обратным выражением: \[Q = R\sqrt {\frac{C}{L}} .\]

   Пример 1

Электрическая цепь состоит из последовательно соединенных резистора сопротивлением \(R = 100\;\text{Ом}\) и катушки с индуктивностью \(L = 50\;\text{Гн}.\) В момент \(t = 0\) подключается источник постоянного напряжения \({V_0} = 200\;\text{В}.\) Найти:

• Закон изменения тока в цепи \(I\left( t \right)\);

• Закон изменения напряжения на резисторе \({V_R}\left( t \right)\) и на катушке индуктивности \({V_L}\left( t \right)\).

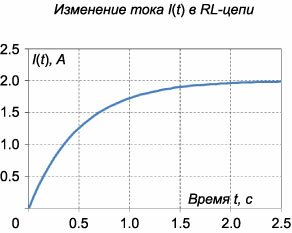
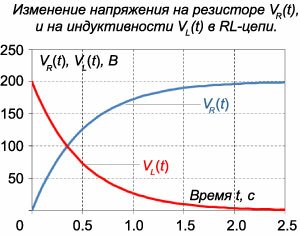
Последовательная \(RL\)-цепь описывается дифференциальным уравнением \[L\frac{{dI}}{{dt}} + RI = {V_0}.\] В соответствии с общей теорией, решением данного уравнения является сумма общего решения однородного уравнения \({I_0}\) и частного решения неоднородного уравнения \({I_1}:\) \(I = {I_0} + {I_1}.\) Общее решение однородного уравнения \[L\frac{{dI}}{{dt}} + RI = 0\] выражается функцией \[{I_0}\left( t \right) = A{e^{ - \frac{R}{L}t}},\] где \(A\) − постоянная интегрирования.

Решение неоднородного уравнения \({I_1}\) соответствует установившемуся режиму, при котором ток в цепи определяется лишь омическим сопротивлением \(R:\) \({I_1} = \frac{{{V_0}}}{R}.\) Тогда полный ток будет изменяться по закону \[I\left( t \right) = {I_0} + {I_1} = A{e^{ - \frac{R}{L}t}} + \frac{{{V_0}}}{R}.\] Постоянная \(A\) определяется из начального условия \(I\left( {t = 0} \right) = 0.\) Следовательно, \[ {0 = A{e^{ - \frac{R}{L} \cdot 0}} + \frac{{{V_0}}}{R},}\;\; {\Rightarrow A = - \frac{{{V_0}}}{R}.} \] Итак, после замыкания цепи ток будет изменяться по закону \[ {I\left( t \right) = - \frac{{{V_0}}}{R}{e^{ - \frac{R}{L}t}} + \frac{{{V_0}}}{R} } = {\frac{{{V_0}}}{R}\left( {1 - {e^{ - \frac{R}{L}t}}} \right) } = {\frac{{200}}{{100}}\left( {1 - {e^{ - \frac{{100}}{{50}}t}}} \right) } = {2\left( {1 - {e^{ - 2t}}} \right)\;\left[ \text{A} \right].} \] График \(I\left( t \right)\) показан на рисунке \(7.\)

Напряжения на резисторе \({V_R}\) и на катушке индуктивности \({V_L}\) определяются следующими формулами: \[ {{V_R}\left( t \right) = I\left( t \right)R = {V_0}\left( {1 - {e^{ - \frac{R}{L}t}}} \right) } = {200\left( {1 - {e^{ - 2t}}} \right)\;\left[ \text{В} \right],} \] \[ {{V_L}\left( t \right) = L\frac{{dI\left( t \right)}}{{dt}} } = {\frac{{L{V_0}}}{R}\frac{d}{{dt}}\left( {1 - {e^{ - \frac{R}{L}t}}} \right) } = {\frac{{\cancel{L}{V_0}}}{\cancel{R}} \cdot \frac{\cancel{R}}{\cancel{L}}{e^{ - \frac{R}{L}t}} } = {{V_0}{e^{ - \frac{R}{L}t}} } = {200{e^{ - 2t}}\;\left[ \text{В} \right].} \] Графики функций \({V_R}\left( t \right)\) и \({V_L}\left( t \right)\) приведены на рисунке \(8.\)

   Пример 2

Электрическая цепь состоит из последовательно соединенных резистора сопротивлением \(R = 100\;\text{Ом}\) и конденсатора \(C = 0.01\;\text{мкФ}.\) В начальный момент подключается источник постоянного напряжения \({V_0} = 200\;\text{В}.\) Найти:

• Закон изменения тока в цепи \(I\left( t \right)\);

• Закон изменения напряжения на резисторе \({V_R}\left( t \right)\) и конденсаторе \({V_C}\left( t \right)\).

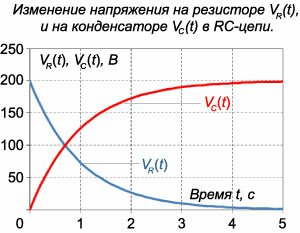
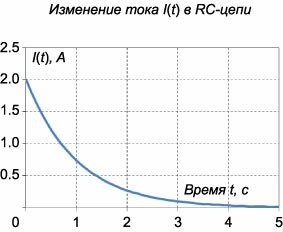
Эта задача похожа на предыдущую и отличается от нее лишь типом электрической цепи. В данной задаче рассматривается \(RC\)-цепь.

Согласно \(2\)-му закону Кирхгофа \[{V_R}\left( t \right) + {V_C}\left( t \right) = {V_0},\] где напряжение на резисторе равно \[{V_R}\left( t \right) = I\left( t \right)R = RC\frac{{d{V_C}}}{{dt}}.\] В результате получаем следующее дифференциальное уравнение для описания переходного процесса в \(RC\)-цепи: \[RC\frac{{d{V_C}}}{{dt}} + {V_C} = {V_0}.\] Решение этого уравнения представляется в виде суммы общего решения однородного уравнения \(V_\text{одн}\) и частного решения неоднородного уравнения \({V_1}.\) Однородное уравнение имеет общее решение в виде \[ {RC\frac{{d{V_C}}}{{dt}} + {V_C} = 0,}\;\; {\Rightarrow \frac{{d{V_C}}}{{dt}} = - \frac{1}{{RC}}{V_C},}\;\; {\Rightarrow \int {\frac{{d{V_C}}}{{{V_C}}}} = - \frac{1}{{RC}}\int {dt} ,}\;\; {\Rightarrow \ln {V_C} = - \frac{t}{{RC}},}\;\; {\Rightarrow {V_\text{одн}} = A{e^{ - \large\frac{t}{{RC}}\normalsize}},} \] где \(A\) − постоянная интегрирования, зависящая от начального условия.

Частное решение неоднородного уравнения соответствует установившемуся режиму, при котором \({\large\frac{{d{V_C}}}{{dt}}\normalsize} = 0.\) Тогда напряжение на резисторе будет равно нулю и все напряжение будет приложено к конденсатору, то есть \({V_C} = {V_0}.\) Таким образом, изменение напряжения на конденсаторе описывается выражением \[{V_C}\left( t \right) = A{e^{ - \large\frac{t}{{RC}}\normalsize}} + {V_0}.\] С учетом начального условия \({V_C}\left( {t = 0} \right) = 0\) находим постоянную \(A:\) \[0 = A \cdot 1 + {V_0},\;\; \Rightarrow A = - {V_0}.\] Следовательно, закон изменения напряжения на конденсаторе будет выглядеть так: \[ {{V_C}\left( t \right) = - {V_0}{e^{ - \large\frac{t}{{RC}}\normalsize}} + {V_0} } = {{V_0}\left( {1 - {e^{ - \large\frac{t}{{RC}}\normalsize}}} \right) } = {200\left( {1 - {e^{ - t}}} \right)\;\left[ \text{В} \right].} \] Напряжение на резисторе определяется формулой \[ {{V_R}\left( t \right) = RC\frac{{d{V_C}}}{{dt}} } = {RC{V_0}\frac{d}{{dt}}\left( {1 - {e^{ - \large\frac{t}{{RC}}\normalsize}}} \right) } = {\cancel{RC}{V_0} \cdot \frac{1}{\cancel{RC}}{e^{ - \large\frac{t}{{RC}}\normalsize}} } = {{V_0}{e^{ - \large\frac{t}{{RC}}\normalsize}} = 200{e^{ - t}}\;\left[ \text{В} \right].} \] Ток в \(RC\)-цепи будет изменяться по закону \[ I\left( t \right) = \frac{{{V_R}\left( t \right)}}{R} = \frac{{{V_0}}}{R}{e^{ - \large\frac{t}{{RC}}\normalsize}} = \frac{{200}}{{100}}{e^{ - t}} = 2{e^{ - t}}\;\left[ \text{A} \right]. \] Графики изменения напряжений \({V_C}\left( t \right),\) \({V_R}\left( t \right)\) и тока \(I\left( t \right)\) показаны на рисунках \(9\) и \(10.\)

   Пример 3

Электрическая цепь состоит из последовательно соединенных резистора сопротивлением \(R = 1\;\text{Ом},\) катушки с индуктивностью \(L = 0.25\;\text{Гн}\) и конденсатора емкостью \(C = 1\;\text{мкФ}.\) Через сколько колебаний амплитуда тока в этом контуре уменьшится в \(e\) раз? В контуре будут происходить затухающие колебания с частотой \[\omega = \sqrt {\frac{1}{{LC}} - \frac{{{R^2}}}{{4{L^2}}}} .\] Амплитуда колебаний будет при этом уменьшаться по закону \[A\left( t \right) = {A_0}{e^{ - {\large\frac{R}{{2L}}\normalsize} t}}.\] Пусть за время \(t\) произошло \(N\) полных колебаний: \[ {t = NT = \frac{{2\pi N}}{\omega } } = {\frac{{2\pi N}}{{\sqrt {\frac{1}{{LC}} - \frac{{{R^2}}}{{4{L^2}}}} }}.} \] Если за это время амплитуда колебаний уменьшилась в \(e\) раз, то справедливо соотношение \[ - \frac{R}{{2L}}t = \frac{R}{{2L}} \cdot \frac{{2\pi N}}{{\sqrt {\frac{1}{{LC}} - \frac{{{R^2}}}{{4{L^2}}}} }} = - 1.\] Отсюда находим число колебаний \(N:\) \[ {N = \frac{L}{{\pi R}}\sqrt {\frac{1}{{LC}} - \frac{{{R^2}}}{{4{L^2}}}} } = {\frac{1}{\pi }\sqrt {\frac{{{L^\cancel{2}}}}{{{R^2}\cancel{L}C}} - \frac{{\cancel{L^2}\cancel{R^2}}}{{4\cancel{R^2}\cancel{L^2}}}} } = {\frac{1}{\pi }\sqrt {\frac{L}{{{R^2}C}} - \frac{1}{4}} } = {\frac{1}{{2\pi }}\sqrt {\frac{{4L}}{{{R^2}C}} - 1} } = {\frac{1}{{2\pi }}\sqrt {\frac{{4 \cdot 0.25}}{{{1^2} \cdot {{10}^{ - 6}}}} - 1} } \approx {\frac{{1000}}{{2\pi }} \approx 159.} \]

   Пример 4

К последовательной цепи, состоящей из сопротивления \(R = 100\;\text{Ом},\) катушки с индуктивностью \(L = 0.4\;\text{Гн}\) и конденсатора емкостью \(C = 200\;\text{мкФ},\) подключен переменный источник напряжения с амплитудой \({E_0} = 128\;\text{В}\) и круговой частотой \(\omega = 250\;\text{Гц}.\) Найти:

• Амплитуду тока в цепи;

• Амплитуду напряжения на конденсаторе.

Вынужденные колебания тока в установившемся режиме происходят с амплитудой \[ {I_0} = \frac{{{E_0}}}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }} = \frac{{128}}{{\sqrt {{{10}^4} + {{\left( {250 \cdot 0.4 - \frac{1}{{250 \cdot 0.2 \cdot {{10}^{ - 3}}}}} \right)}^2}} }} = \frac{{128}}{{\sqrt {{{10}^4} + {{\left( {100 - 20} \right)}^2}} }} = \frac{{128}}{{\sqrt {16400} }} \approx 1\;\left[ \text{A} \right]. \] Амплитуда колебаний напряжения на конденсаторе будет составлять \[{V_C} = \frac{{{q_0}}}{C} = \frac{{{I_0}}}{{\omega C}} = \frac{1}{{250 \cdot 0,2 \cdot {{10}^{ - 3}}}} = 20\;\left[ \text{В} \right].\]