Закон охлаждения Ньютона

В конце \(17\) века британский ученый Исаак Ньютон изучал охлаждение тел. Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать в виде дифференциального уравнения: \[\frac{{dQ}}{{dt}} = \alpha A\left( {{T_S} - T} \right),\] где \(Q\) − количество теплоты, \(A\) − площадь поверхности тела, через которую передается тепло, \(T\) − температура тела, \({{T_S}}\) − температура окружающей среды, \(\alpha\) − коэффициент теплопередачи, зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов.

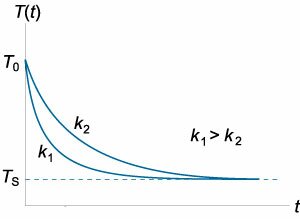
Поскольку \(Q = CT,\) где \(C\) − теплоемкость тела, то дифференциальное уравнение можно записать как \[\frac{{dT}}{{dt}} = \frac{{\alpha A}}{C}\left( {{T_S} - T} \right) = k\left( {{T_S} - T} \right).\] Решение данного уравнение имеет вид: \[T\left( t \right) = {T_S} + \left( {{T_0} - {T_S}} \right){e^{ - kt}},\] где \({T_0}\) обозначает начальную температуру тела.

Таким образом, температура тела уменьшается экспоненциально по мере охлаждения, приближаясь к температуре окружающей среды. Скорость охлаждения зависит от параметра \(k = \large\frac{{\alpha A}}{C}\normalsize\) (коэффициента теплопроводности). С увеличением коэффициента \(k\) (например, вследствие увеличения площади поверхности), тело будет охлаждаться быстрее (рисунок \(1\).)

   Пример 1

Температура тела уменьшилась с \(200^\circ\) до \(100^\circ\) за первый час. Определить на сколько градусов понизится температура еще через один час, если температура окружающей среды \(0^\circ?\) Мы решим задачу сначала для случая произвольной температуры окружающей среды, а затем вычислим конечную температуру тела при температуре среды \(0^\circ.\)

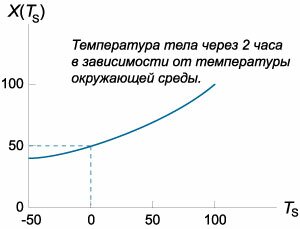
Пусть начальная температура нагретого тела составляет \({T_0} = 200^\circ.\) Последующее изменение температуры описывается формулой: \[ {T\left( t \right) = {T_S} + \left( {{T_0} - {T_S}} \right){e^{ - kt}} } = {{T_S} + \left( {200^\circ - {T_S}} \right){e^{ - kt}}.} \] В конце первого часа тело охладилось до \(100^\circ.\) Следовательно, можно записать следующее соотношение: \[ {T\left( {t = 1} \right) = 100^\circ = {T_S} + \left( {200^\circ - {T_S}} \right){e^{ - k \cdot 1}},}\;\; {\Rightarrow 100^\circ = {T_S} + \left( {200^\circ - {T_S}} \right){e^{ - k}}.} \] Спустя \(2\) часа температура тела становится равной \(X\) градусов: \[X = {T_S} + \left( {200^\circ - {T_S}} \right){e^{ - 2k}}.\] Таким образом, мы получили систему двух уравнений с тремя неизвестными: \({T_S},\) \(k\) и \(X:\) \[\left\{ \begin{array}{l} 100 = {T_S} + \left( {200 - {T_S}} \right){e^{ - k}}\\ X = {T_S} + \left( {200 - {T_S}} \right){e^{ - 2k}} \end{array} \right..\] Мы не можем однозначно определить температуру тела \(X\) через \(2\) часа из данной системы. Однако можно вывести зависимость \(X\) от температуры окружающей среды \({T_S}.\) Выразим функцию \({e^{ - k}}\) из первого уравнения: \[{e^{ - k}} = \frac{{100 - {T_S}}}{{200 - {T_S}}}.\] Тогда \[{e^{ - 2k}} = {\left( {{e^{ - k}}} \right)^2} = {\left( {\frac{{100 - {T_S}}}{{200 - {T_S}}}} \right)^2}.\] Следовательно, зависимость \(X\left( {{T_S}} \right)\) имеет вид: \[ {X\left( {{T_S}} \right) = {T_S} + \left( {200 - {T_S}} \right){\left( {\frac{{100 - {T_S}}}{{200 - {T_S}}}} \right)^2} } = {{T_S} + \frac{{{{\left( {100 - {T_S}} \right)}^2}}}{{200 - {T_S}}}.} \] Если, например, положить температуру окружающей среды равной нулю, то температура тела через два часа будет составлять \[ {X\left( {{T_S} = 0} \right) = 0 + \frac{{{{\left( {100 - 0} \right)}^2}}}{{200 - 0}} } = {\frac{{10000}}{{200}} = 50^\circ.} \] Зависимость температуры тела \(X\) от температуры окружающей среды в данной задаче показана выше на рисунке \(2.\)

   Пример 2

Тело с начальной температурой \({T_0}\) помещено в комнату с температурой \({T_{S0}}\) и начинает охлаждаться в соответствии с законом Ньютона с постоянной величиной \(k.\) При этом температура комнаты медленно растет по линейному закону \[{T_S} = {T_{S0}} + \beta t,\] где \(\beta\) − известный параметр. Определить момент времени \(\tau,\) когда температура тела и окружающей среды сравняются. Прежде всего, отметим разницу со случаем когда тело охлаждается в среде, температура которой постоянна. В этом случае температура тела формально будет бесконечно долго приближаться к температуре окружающей среды. В нашей же задаче температура среды линейно возрастает. Поэтому, рано или поздно температура тела станет равной температуре среды, то есть задача имеет решение. Будем считать также, что соблюдается квазистационарный режим, т.е. все переходные процессы в системе быстро затухают.

В таком случае процесс можно описать дифференциальным уравнением: \[\frac{{dT}}{{dt}} = k\left( {{T_S} - T} \right).\] По условию задачи, \({T_S} = {T_{S0}} + \beta t.\) Следовательно, последнее уравнение можно записать в виде: \[ {\frac{{dT}}{{dt}} = k\left( {{T_{S0}} + \beta t - T} \right)}\;\; {\text{или}\;\;T' + kT = k{T_{S0}} + k\beta t.} \] Мы получили линейное дифференциальное уравнение, которое можно решить, например, с помощью интегрирующего множителя: \[u\left( t \right) = {e^{\int {kdt} }} = {e^{kt}}.\] Общее решение уравнения записывается в форме \[ {T\left( t \right) = \frac{{\int {{e^{kt}}\left( {k{T_{S0}} + k\beta t} \right)dt} + C}}{{{e^{kt}}}} } = {\frac{{k{T_{S0}}\int {{e^{kt}}dt} + k\beta \int {{e^{kt}}tdt} + C}}{{{e^{kt}}}}.} \] Второй интеграл в числителе находится интегрированием по частям: \[ {\int {\underbrace {{e^{kt}}}_{u'}\underbrace t_vdt} } = {\left[ {\begin{array}{*{20}{l}} {u' = {e^{kt}}}\\ {u = \frac{1}{k}{e^{kt}}}\\ {v = t}\\ {v' = 1} \end{array}} \right] } = {\frac{1}{k}{e^{kt}}t - \int {\frac{1}{k}{e^{kt}}dt} } = {\frac{1}{k}{e^{kt}}t - \frac{1}{{{k^2}}}{e^{kt}} } = {\frac{1}{k}{e^{kt}}\left( {t - \frac{1}{k}} \right).} \] Таким образом, закон охлаждения тела имеет следующий вид: \[ {T\left( t \right) } = {\frac{{k{T_{S0}} \cdot \frac{1}{k}{e^{kt}} + k\beta \cdot \frac{1}{k}{e^{kt}}\left( {t - \frac{1}{k}} \right) + C}}{{{e^{kt}}}} } = {{T_{S0}} + \beta t - \frac{\beta }{k} + C{e^{ - kt}}.} \] Постоянная \(C\) определяется из начального условия \(T\left( {t = 0} \right) = {T_0}.\) Тогда \[C = {T_0} - {T_{S0}} + \frac{\beta }{k}.\] Итак, процесс охлаждения тела описывается формулой \[T\left( t \right) = {T_{S0}} + \beta t - \frac{\beta }{k} + \left( {{T_0} - {T_{S0}} + \frac{\beta }{k}} \right){e^{ - kt}}.\] В момент \(\tau,\) температуры тела и окружающей среды становятся равными друг другу: \[T\left( \tau \right) = {T_{S0}} + \beta \tau .\] Время \(\tau\) определяется из уравнения: \[\require{cancel} {\cancel{{T_{S0}} + \beta \tau} = \cancel{{T_{S0}} + \beta \tau} - \frac{\beta }{k} + \left( {{T_0} - {T_{S0}} + \frac{\beta }{k}} \right){e^{ - k\tau }},}\;\; {\Rightarrow \left( {{T_0} - {T_{S0}} + \frac{\beta }{k}} \right){e^{ - k\tau }} = \frac{\beta }{k},}\;\; {\Rightarrow \frac{k}{\beta }\left( {{T_0} - {T_{S0}} + \frac{\beta }{k}} \right) = {e^{k\tau }},}\;\; {\Rightarrow \frac{k}{\beta }\left( {{T_0} - {T_{S0}}} \right) + 1 = {e^{k\tau }},}\;\; {\Rightarrow \tau = \frac{1}{k}\ln \left[ {\frac{k}{\beta }\left( {{T_0} - {T_{S0}}} \right) + 1} \right].} \] Мы можем сделать оценку времени \(\tau\) для некоторых типичных значений параметров: \[ {{T_{S0}} = 20^{\circ}C,\;\;\;k = \frac{1}{5}\,\text{мин}^{-1},}\;\;\; {\beta = 2\,\frac{\text{град}}{\text{мин}},\;\;\;{T_0} = 200^{\circ}C.} \] В результате получаем: \[ {\tau = \frac{1}{k}\ln \left[ {\frac{k}{\beta }\left( {{T_0} - {T_{S0}}} \right) + 1} \right] } = {\frac{1}{{\frac{1}{5}}}\ln \left[ {\frac{{\frac{1}{5}}}{2}\left( {200 - 20} \right) + 1} \right] } = {5\ln \left[ {\frac{1}{{10}} \cdot 180 + 1} \right] } = {5\ln 19 } \approx {5 \cdot 2.944 } \approx {14.77\left[ {\text{мин}} \right].} \]