|
Закон всемирного тяготения
|
||||||||||||
|
Сила притяжения и гравитационный потенциал
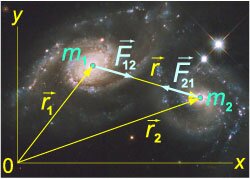
Закон всемирного тяготения был сформулирован Исааком Ньютоном (\(1643-1727\)) и опубликован в \(1687\) году. В соответствии с этим законом, два точечных тела притягиваются друг к другу с силой, которая прямо пропорциональна массам этих тел \({m_1}\) и \({m_2}\) и обратно пропорциональна квадрату расстояния между ними: \[F = G\frac{{{m_1}{m_2}}}{{{r^2}}}.\] Здесь \(r\) − расстояние между данными телами, \(G\) − гравитационная постоянная, значение которой, найденное экспериментальным путем, составляет \(G = 6,67 \times {10^{ - 11}}\;\large\frac{{{\text{м}^3}}}{{\text{кг} \cdot {\text{с}^2}}}\normalsize.\)Сила гравитационного притяжения является центральной силой, т.е. направлена вдоль прямой, проходящей через центры взаимодействующих тел.
При большом различии в массах тел можно пренебречь массой меньшего тела в правой части полученного уравнения. Так, например, масса Солнца в \(333000\) раз больше массы Земли. В этом случае дифференциальное уравнение можно записать в более простом виде: \[\frac{{{d^2}\mathbf{r}}}{{d{t^2}}} = - G\frac{{{M_\text{C}}}}{{{r^3}}}\mathbf{r},\] где \({M_\text{C}}\) − масса Солнца. Гравитационное взаимодействие тел осуществляется посредством гравитационного поля, которое можно описать с помощью скалярного потенциала \(\varphi.\) Сила, действующая на тело массой \(m,\) помещенное в поле с потенциалом \(\varphi,\) будет равна \[\mathbf{F} = m\mathbf{a} = - m\,\mathbf{\text{grad}}\,\varphi .\] В случае точечной массы \(M\) потенциал гравитационного поля определяется формулой \[\varphi = - \frac{{GM}}{r}.\] Последняя формула справедлива и для распределенных тел, обладающих центральной симметрией − таких, например, как планеты или звезды.
Законы Кеплера
Основные законы движения планет были установлены Иоганном Кеплером (\(1571-1630\)) на основе анализа астрономических наблюдений Тихо Браге (\(1546-1601\)). В \(1609\) году Кеплер сформулировал первые два закона. Третий закон был открыт в \(1619\) году. Позже, в конце \(17\) века, Исаак Ньютон математически доказал, что все три закона Кеплера являются следствием закона всемирного тяготения.
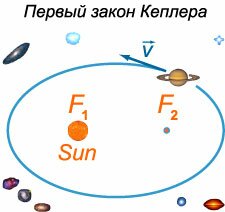
Первый закон Кеплера
Орбита каждой планеты в Солнечной системе представляет собой эллипс, в одном из фокусов которого находится Солнце (рисунок \(3\)).
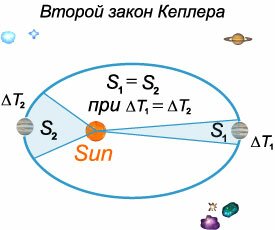
Второй закон Кеплера
Радиус-вектор, соединяющий Солнце и планету, за равные промежутки времени описывает равные площади. На рисунке \(4\) показаны два сектора эллипса, соответствующие одинаковым интервалам времени. Согласно второму закону Кеплера, площади этих секторов равны.
Третий закон Кеплера
Квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси ее орбиты: \[{T^2} \propto {a^3}.\] Коэффициент пропорциональности является одним и тем же для всех планет Солнечной системы. Поэтому для любых двух планет справедливо соотношение \[\frac{{T_2^2}}{{T_1^2}} = \frac{{a_2^3}}{{a_1^3}}.\]
|
||||||||||||
|
Пример
|
||||||||||||
|
Небольшое космическое тело под действием гравитационной силы начинает из состояния покоя падать на Землю. Начальное растояние до центра Земли равно \(L.\) Определить скорость в момент падения и время падения тела на Землю.
Решение. Это нелинейное уравнение относится к типу \(y'' = f\left( y \right)\) и допускает понижение порядка. Учитывая, что \[\frac{{{d^2}r}}{{d{t^2}}} = \frac{{dv}}{{dt}} = \frac{{dv}}{{dr}}\frac{{dr}}{{dt}} = v\frac{{dv}}{{dr}},\] уравнение принимает вид: \[v\frac{{dv}}{{dr}} = - G\frac{{{M_\text{З}}}}{{{r^2}}}.\] Интегрируем его, разделяя переменные, при начальном условии \(v\left( {r = L} \right) = 0:\) \[ {vdv = - G{M_\text{З}}\frac{{dr}}{{{r^2}}},}\;\; {\Rightarrow \int {vdv} = - G{M_\text{З}}\int {\frac{{dr}}{{{r^2}}}} ,}\;\; {\Rightarrow \frac{{{v^2}}}{2} = \frac{{G{M_\text{З}}}}{r} + {C_1},}\;\; {\Rightarrow v = \sqrt {\frac{{2G{M_\text{З}}}}{r} + {C_1}} .} \] Учитывая начальное условие, имеем: \[ {0 = \sqrt {\frac{{2G{M_\text{З}}}}{L} + {C_1}} ,}\;\; {\Rightarrow {C_1} = - \frac{{2G{M_\text{З}}}}{L},}\;\; {\Rightarrow v = \sqrt {2G{M_\text{З}}\left( {\frac{1}{r} - \frac{1}{L}} \right)} .} \] В предельном случае при \(L \to \infty\) формула для скорости упрощается: \[v = \sqrt {\frac{{2G{M_\text{З}}}}{r}} .\] Данное выражение можно переписать через ускорение свободного падения \(g = \large\frac{{G{M_\text{З}}}}{{R_\text{З}^2}}\normalsize,\) где \({R_\text{З}}\) − радиус Земли. Тогда \[v = \sqrt {\frac{{2G{M_\text{З}}}}{r}} = \sqrt {\frac{{2gR_\text{З}^2}}{r}} .\] Отсюда получаем, что при движении из бесконечности скорость тела в момент падения на землю будет составлять \[v\left( {r = {R_\text{З}}} \right) = \sqrt {\frac{{2gR_\text{З}^2}}{{{R_1}}}} = \sqrt {2g{R_\text{З}}} ,\] то есть будет равна второй космической скорости \(v \approx 10,2\,\large\frac{\text{км}}{\text{с}}\normalsize.\) При конечном значении \(L\) скорость тела в момент падения будет меньше второй космической скорости: \[ {v\left( {r = {R_\text{З}}} \right) = \sqrt {2G{M_\text{З}}\left( {\frac{1}{{{R_\text{З}}}} - \frac{1}{L}} \right)} } = {\sqrt {2gR_\text{З}^2\left( {\frac{1}{{{R_\text{З}}}} - \frac{1}{L}} \right)} } = {\sqrt {2g{R_\text{З}}\left( {1 - \frac{{{R_\text{З}}}}{L}} \right)} } = {\sqrt {2g{R_\text{З}}} \sqrt {1 - \frac{{{R_\text{З}}}}{L}} .} \] Определим теперь время падения тела на Землю, считая что начальное расстояние до центра Земли равно \(L.\) Поскольку \(\large\frac{{dr}}{{dt}}\normalsize = - v,\) получаем следующее дифференциальное уравнение, описывающее закон движения тела вдоль радиальной оси: \[ {\frac{{dr}}{{dt}} = - {R_\text{З}}\sqrt {2g} \sqrt {\frac{1}{r} - \frac{1}{L}} ,}\;\; {\Rightarrow \frac{{dr}}{{\sqrt {\frac{1}{r} - \frac{1}{L}} }} = - {R_\text{З}}\sqrt {2g} dt,} \] где расстояние \(r\) изменяется от \(L\) до \({R_\text{З}}.\) Чтобы проинтегрировать данное уравнение, сделаем замену переменной: \[ {\frac{1}{r} - \frac{1}{L} = {z^2},}\;\; {\Rightarrow \frac{1}{r} = {z^2} + \frac{1}{L},}\;\; {\Rightarrow - \frac{1}{{{r^2}}}dr = 2zdz,}\;\; {\Rightarrow \frac{1}{{{r^2}}}dr = - 2zdz,}\;\; {\Rightarrow {\left( {{z^2} + \frac{1}{L}} \right)^2}dr = - 2zdz,}\;\; {\Rightarrow dr = - \frac{{2zdz}}{{{{\left( {{z^2} + \frac{1}{L}} \right)}^2}}}.} \] Тогда уравнение переписывается в виде \[ {- \frac{{2zdz}}{{{{\left( {{z^2} + \frac{1}{L}} \right)}^2}z}} = - {R_\text{З}}\sqrt {2g} dt,}\;\; {\Rightarrow 2\int {\frac{{dz}}{{{{\left( {{z^2} + \frac{1}{L}} \right)}^2}}}} = {R_\text{З}}\sqrt {2g} t + C.} \] Полученный интеграл является табличным. Известно, что \[\int {\frac{{dx}}{{{{\left( {{x^2} + {a^2}} \right)}^2}}} = \frac{x}{{2{a^2}\left( {{x^2} + {a^2}} \right)}} + \frac{1}{{2{a^3}}}\arctan \frac{x}{a}.} \] Следовательно, в нашем случае мы имеем \[ {\int {\frac{{dz}}{{{{\left( {{z^2} + \frac{1}{L}} \right)}^2}}}} } = {\frac{z}{{\frac{2}{L}\left( {{z^2} + \frac{1}{L}} \right)}} + \frac{{{L^{\large\frac{3}{2}\normalsize}}}}{2}\arctan \left( {z\sqrt L } \right).} \] Подставляя найденный интеграл, запишем уравнение в виде \[ {2\left[ {\frac{z}{{\frac{2}{L}\left( {{z^2} + \frac{1}{L}} \right)}} + \frac{{{L^{\large\frac{3}{2}\normalsize}}}}{2}\arctan \left( {z\sqrt L } \right)} \right] = {R_\text{З}}\sqrt {2g} t + C,}\;\; {\Rightarrow \frac{{zL}}{{{z^2} + \frac{1}{L}}} + {L^{\large\frac{3}{2}\normalsize}}\arctan \left( {z\sqrt L } \right) = {R_\text{З}}\sqrt {2g} t + C.} \] Перейдем обратно от переменной \(z\) к переменной \(r:\) \[ {\frac{{L\sqrt {\frac{1}{r} - \frac{1}{L}} }}{{\frac{1}{r}}} + {L^{\large\frac{3}{2}\normalsize}}\arctan \left( {\sqrt L \sqrt {\frac{1}{r} - \frac{1}{L}} } \right) = {R_\text{З}}\sqrt {2g} t + C,}\;\; {\Rightarrow r\sqrt L \sqrt {\frac{L}{r} - 1} + {L^{\large\frac{3}{2}\normalsize}}\arctan \sqrt {\frac{L}{r} - 1} = {R_\text{З}}\sqrt {2g} t + C.} \] Учитывая начальное условие \(r\left( {t = 0} \right) = L,\) находим, что постоянная \(C\) равна нулю. Поскольку в момент падения тела \(r\left( {t = T} \right) = {R_\text{З}},\) то для времени падения \(T\) получаем следующее выражение: \[ {{R_\text{З}}\sqrt L \sqrt {\frac{L}{{{R_\text{З}}}} - 1} + {L^{\large\frac{3}{2}\normalsize}}\arctan \sqrt {\frac{L}{{{R_\text{З}}}} - 1} = {R_\text{З}}\sqrt {2g} T,}\;\; {\Rightarrow T = \frac{{{R_\text{З}}\sqrt L \sqrt {\frac{L}{{{R_\text{З}}}} - 1} + {L^{\large\frac{3}{2}\normalsize}}\arctan \sqrt {\frac{L}{{{R_\text{З}}}} - 1} }}{{{R_\text{З}}\sqrt {2g} }}.} \] После небольшого упрощения точная формула для времени падения записывается как \[T = \sqrt {\frac{L}{{2g}}} \left[ {\sqrt {\frac{L}{{{R_\text{З}}}} - 1} + \frac{L}{{{R_\text{З}}}}\arctan \sqrt {\frac{L}{{{R_\text{З}}}} - 1} } \right].\] При больших значениях отношения \({\large\frac{L}{{{R_\text{З}}}}\normalsize}\) (при этом функция \(\arctan\) стремится к \(\large\frac{\pi }{2}\normalsize\)) получаем более простое выражение: \[ {T \approx \sqrt {\frac{L}{{2g}}} \left[ {\sqrt {\frac{L}{{{R_\text{З}}}} - 1} + \frac{L}{{{R_\text{З}}}}\frac{\pi }{2}} \right] } \approx \frac{\pi }{2}{\sqrt {\frac{L}{{2g}}} \frac{L}{{{R_\text{З}}}}.} \] Для примера, оценим с помощью этой формулы время падения тела с расстояния \(100000\;\text{км}:\) \[ {T \approx \frac{\pi }{2}\sqrt {\frac{L}{{2g}}} \frac{L}{{{R_\text{З}}}} } = {\frac{\pi }{2} \cdot \sqrt {\frac{{{{10}^8}}}{{2 \cdot 10}}} \cdot \frac{{{{10}^8}}}{{6,4 \cdot {{10}^6}}} } \approx {54900\;\text{сек} = 15,2\;\text{часа}.} \] |
||||||||||||