Динамика цен и запасов

С помощью систем дифференциальных уравнений можно описывать реальные экономические процессы. Рассмотрим для примера одну из возможных моделей, в которой цены, объем продаж и запасы товара на складе определенным образом зависят друг от друга и могут изменяться во времени. В условиях эластичного рынка объем продаж зависит от цены товара или услуги. Такую зависимость можно представить, например, в виде \[\frac{{dS}}{{dt}} = \beta \left( {P - {P^*}} \right),\] где \(S\) − объем продаж за единицу времени, \(P\) − текущая цена, \({P^*}\) − некоторая равновесная цена, близкая к среднерыночной, \(\beta\) − коэффициент пропорциональности. Здесь функция \(S\left( t \right)\) имеет смысл текущей скорости продажи. То есть, объем продаж товара за промежуток времени \(\Delta t\) будет равен \(S\left( t \right)\Delta t.\) Размерность коэффициента \(\beta\) зависит от единиц \(S\) и \(P.\) Если рассматривать \(S\) и \(P\) как безразмерные величины, а время \(t\) измерять в днях, то размерность \(\beta\) будет составлять \(\left[ {\large\frac{1}{\text{день}}\normalsize} \right].\)

Данное дифференциальное уравнение "работает" следующим образом. Изменение скорости продажи \(\large\frac{{dS}}{{dt}}\normalsize\) зависит от величины отклонения текущей цены \(P\) от равновесного значения \({P^*}.\) Пусть коэффициент \(\beta\) отрицателен: \(\beta < 0.\) Тогда в интервале значений \({P < {P^*}}\) при понижении цены скорость продажи будет возрастать, и наоборот. Такая агрессивная маркетинговая стратегия часто применяется, например, в сезон распродаж (рисунок \(1\)). При реализации описанного подхода бизнес может преследовать еще одну цель − поддерживать уровень запасов товара на некотором достаточно низком уровне \({I^*}\) с помощью изменения цены товара. Такой режим управления можно описать похожим дифференциальным уравнением \[\frac{{dP}}{{dt}} = \alpha \left( {I - {I^*}} \right),\] где \(\alpha\) − коэффициент пропорциональности, который является отрицательным. В этом случае при дефиците товара на складе (при \({I < {I^*}}\)) цена будет возрастать, а при его избытке (\({I > {I^*}}\)) − уменьшаться. Размерность коэффициента \(\alpha,\) также как и коэффициента \(\beta,\) составляет \(\left[ {\large\frac{1}{\text{день}}\normalsize} \right].\)

К записанным уравнениям необходимо добавить еще одно уравнение, описывающее баланс товаров на складе: \[\frac{{dI}}{{dt}} = Q - S,\] где \(Q\) − скорость поступления товаров от производителя или поставщика, \(S\) − уже рассмотренная выше скорость продажи товара.

В результате мы получаем систему \(3\) дифференциальных уравнений: \[ {\frac{{dI}}{{dt}} = Q - S,}\;\; {\frac{{dP}}{{dt}} = \alpha \left( {I - {I^*}} \right),}\;\; {\frac{{dS}}{{dt}} = \beta \left( {P - {P^*}} \right).} \] Построим далее ее общее решение и исследуем поведение функций \(I\left( t \right),\) \(P\left( t \right),\) \(S\left( t \right).\) Записанная система относится к классу линейных неоднородных систем с постоянными коэффициентами. Ее можно записать в матричной форме: \[\mathbf{Z'}\left( t \right) = A\mathbf{Z}\left( t \right) + \mathbf{F},\] где \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right),}\;\; {A = \left( {\begin{array}{*{20}{c}} 0&0&{ - 1}\\ \alpha &0&0\\ 0&\beta &0 \end{array}} \right),}\;\; {\mathbf{F} = \left( {\begin{array}{*{20}{c}} Q\\ { - \alpha {I^*}}\\ { - \beta {P^*}} \end{array}} \right).} \] Построим сначала решение однородной системы. Найдем собственные значения матрицы \(A:\) \[ {\det \left( {A - \lambda I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - \lambda }&0&{ - 1}\\ \alpha &{ - \lambda }&0\\ 0&\beta &{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow \left( { - \lambda } \right)\left| {\begin{array}{*{20}{c}} { - \lambda }&0\\ \beta &{ - \lambda } \end{array}} \right| - \alpha \left| {\begin{array}{*{20}{c}} 0&{ - 1}\\ \beta &{ - \lambda } \end{array}} \right| = 0,}\;\; {\Rightarrow - \lambda \cdot {\lambda ^2} - \alpha \cdot \beta = 0,}\;\; {\Rightarrow - {\lambda ^3} - \alpha \beta ,}\;\; {\Rightarrow {\lambda ^3} = - \alpha \beta ,}\;\; {\Rightarrow {\lambda _1} = - \sqrt[\large 3\normalsize]{{\alpha \beta }}.} \] Как видно, характеристическое уравнение имеет один корень с алгебраической кратностью \(k = 3.\) Вычислим ранг матрицы \({A - {\lambda _1}I}:\) \[ {\left( {\begin{array}{*{20}{c}} {\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0&{ - 1}\\ \alpha &{\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) \cdot \begin{array}{*{20}{l}} {}\\ \small{\left( { - \frac{{\sqrt[3]{\beta }}}{{\sqrt[3]{{{\alpha ^2}}}}}} \right)}\normalsize\\ {} \end{array} } \sim {\left( {\begin{array}{*{20}{c}} {\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0&{ - 1}\\ { - \sqrt[\large 3\normalsize]{{\alpha \beta }}}&{ - \frac{{\sqrt[\large 3\normalsize]{{{\beta ^2}}}}}{{\sqrt[\large 3\normalsize]{\alpha }}}}&0\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right)\begin{array}{*{20}{l}} {}\\ \small{{R_2} + {R_1}}\normalsize\\ {} \end{array} } \sim {\left( {\begin{array}{*{20}{c}} {\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0&{ - 1}\\ 0&{ - \frac{{\sqrt[\large 3\normalsize]{{{\beta ^2}}}}}{{\sqrt[\large 3\normalsize]{\alpha }}}}&{ - 1}\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) \cdot \begin{array}{*{20}{l}} {}\\ \small{\left( { - \sqrt[3]{{\alpha \beta }}} \right)}\normalsize\\ {} \end{array} } \sim {\left( {\begin{array}{*{20}{c}} {\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0&{ - 1}\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}}\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) } \sim {\left( {\begin{array}{*{20}{c}} {\sqrt[\large 3\normalsize]{{\alpha \beta }}}&0&{ - 1}\\ 0&\beta &{\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right).} \] Ранг равен \(2.\) Тогда геометрическая кратность будет равна \[s = n - \text{rank}\left( {A - {\lambda _1}I} \right) = 3 - 2 = 1.\] Такой матрице соответствует жорданова клетка размером \(3 \times 3\) (случай \(8\) на странице Построение общего решения системы уравнений с помощью жордановой формы), т.е. матрица \(A\) будет иметь один собственный вектор и два присоединенных вектора.

Для построения общего решения мы воспользуемся методом неопределенных коэффициентов. Будем искать решение в виде \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{\mathbf{M}_{k - s}}\left( t \right){e^{{\lambda _1}t}} } = {{\mathbf{M}_{3 - 1}}\left( t \right){e^{{\lambda _1}t}} } = {{\mathbf{M}_2}\left( t \right){e^{{\lambda _1}t}},} \] где \({\mathbf{M}_{k - s}}\left( t \right)\) − векторный многочлен, который в нашем случае является квадратичной функцией: \[{\mathbf{M}_2}\left( t \right) = {\mathbf{A}_0} + {\mathbf{A}_1}t + {\mathbf{A}_2}{t^2}.\] Определим значения коэффициентов в векторном многочлене. Пусть векторы \({\mathbf{A}_0},\) \({\mathbf{A}_1},\) \({\mathbf{A}_2}\) имеют координаты: \[ {{\mathbf{A}_0} = \left( {\begin{array}{*{20}{c}} {{a_0}}\\ {{b_0}}\\ {{c_0}} \end{array}} \right),}\;\; {{\mathbf{A}_1} = \left( {\begin{array}{*{20}{c}} {{a_1}}\\ {{b_1}}\\ {{c_1}} \end{array}} \right),}\;\; {{\mathbf{A}_2} = \left( {\begin{array}{*{20}{c}} {{a_2}}\\ {{b_2}}\\ {{c_2}} \end{array}} \right),}\;\; {\Rightarrow \mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {\left( {\begin{array}{*{20}{c}} {\left( {{a_0} + {a_1}t + {a_2}{t^2}} \right){e^{{\lambda _1}t}}}\\ {\left( {{b_0} + {b_1}t + {b_2}{t^2}} \right){e^{{\lambda _1}t}}}\\ {\left( {{c_0} + {c_1}t + {c_2}{t^2}} \right){e^{{\lambda _1}t}}} \end{array}} \right).} \] Найдем производные: \[ {\frac{{dI}}{{dt}} = \left( {{a_1} + 2{a_2}t} \right){e^{{\lambda _1}t}} } + {{\lambda _1}\left( {{a_0} + {a_1}t + {a_2}{t^2}} \right){e^{{\lambda _1}t}},} \] \[ {\frac{{dP}}{{dt}} = \left( {{b_1} + 2{b_2}t} \right){e^{{\lambda _1}t}} } + {{\lambda _1}\left( {{b_0} + {b_1}t + {b_2}{t^2}} \right){e^{{\lambda _1}t}},} \] \[ {\frac{{dS}}{{dt}} = \left( {{c_1} + 2{c_2}t} \right){e^{{\lambda _1}t}} } + {{\lambda _1}\left( {{c_0} + {c_1}t + {c_2}{t^2}} \right){e^{{\lambda _1}t}}.} \] Подставляя функции \(I\left( t \right),\) \(P\left( t \right),\) \(S\left( t \right)\) и их производные в исходную однородную систему и сокращая на \({e^{{\lambda _1}t}},\) получаем: \[ {\left\{ \begin{array}{l} \frac{{dI}}{{dt}} = - S\\ \frac{{dP}}{{dt}} = \alpha I\\ \frac{{dS}}{{dt}} = \beta P \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{a_1} + 2{a_2}t + {\lambda _1}\left( {{a_0} + {a_1}t + {a_2}{t^2}} \right) = - \left( {{c_0} + {c_1}t + {c_2}{t^2}} \right)}\\ {{b_1} + 2{b_2}t + {\lambda _1}\left( {{b_0} + {b_1}t + {b_2}{t^2}} \right) = \alpha \left( {{a_0} + {a_1}t + {a_2}{t^2}} \right)}\\ {{c_1} + 2{c_2}t + {\lambda _1}\left( {{c_0} + {c_1}t + {c_2}{t^2}} \right) = \beta \left( {{b_0} + {b_1}t + {b_2}{t^2}} \right)} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{a_1} + 2{a_2}t + {\lambda _1}{a_0} + {\lambda _1}{a_1}t + {\lambda _1}{a_2}{t^2} = - {c_0} - {c_1}t - {c_2}{t^2}}\\ {{b_1} + 2{b_2}t + {\lambda _1}{b_0} + {\lambda _1}{b_1}t + {\lambda _1}{b_2}{t^2} = \alpha {a_0} + \alpha {a_1}t + \alpha {a_2}{t^2}}\\ {{c_1} + 2{c_2}t + {\lambda _1}{c_0} + {\lambda _1}{c_1}t + {\lambda _1}{c_2}{t^2} = \beta {b_0} + \beta {b_1}t + \beta {b_2}{t^2}} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{a_1} + {\lambda _1}{a_0} = - {c_0}}\\ {2{a_2} + {\lambda _1}{a_1} = - {c_1}}\\ {{\lambda _1}{a_2} = - {c_2}}\\ {{b_1} + {\lambda _1}{b_0} = \alpha {a_0}}\\ {2{b_2} + {\lambda _1}{b_1} = \alpha {a_1}}\\ {{\lambda _1}{b_2} = \alpha {a_2}}\\ {{c_1} + {\lambda _1}{c_0} = \beta {b_0}}\\ {2{c_2} + {\lambda _1}{c_1} = \beta {b_1}}\\ {{\lambda _1}{c_2} = \beta {b_2}} \end{array}} \right..} \] Пусть \({a_0} = {C_1},\) \({a_1} = {C_2},\) \({a_2} = {C_3}.\) Выразим остальные коэффициенты через \({C_1},\) \({C_2},\) \({C_3},\) учитывая, что собственное значение равно \({\lambda _1} = - \sqrt[\large 3\normalsize]{{\alpha \beta }}:\) \[ {{c_0} = - \left( {{a_1} + {\lambda _1}{a_0}} \right) } = { - {C_2} - {\lambda _1}{C_1} } = { - {C_2} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_1},} \] \[ {{c_1} = - \left( {2{a_2} + {\lambda _1}{a_1}} \right) } = { - 2{C_3} - {\lambda _1}{C_2} } = { - 2{C_3} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_2},} \] \[{c_2} = - {\lambda _1}{a_2} = - {\lambda _1}{C_3} = \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_3},\] \[ {{b_2} = \frac{\alpha }{{{\lambda _1}}}{a_2} = \frac{\alpha }{{{\lambda _1}}}{C_3} } = {\frac{\alpha }{{\left( { - \sqrt[\large 3\normalsize]{{\alpha \beta }}} \right)}}{C_3} } = { - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_3},} \] \[ {{b_0} = \frac{1}{\beta }\left( {{c_1} + {\lambda _1}{c_0}} \right) } = {\frac{1}{\beta }\left( { - 2{C_3} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_2}} \right) + \frac{{\left( { - \sqrt[\large 3\normalsize]{{\alpha \beta }}} \right)}}{\beta }\left( {-{C_2} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_1}} \right) } = { - \frac{2}{\beta }{C_3} + \sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_2} + \sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_2} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_1} } = { - \frac{2}{\beta }{C_3} + 2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_2} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_1},} \] \[ {{b_1} = \frac{1}{\beta }\left( {2{c_2} + {\lambda _1}{c_1}} \right) } = {\frac{2}{\beta }{c_2} + \frac{{{\lambda _1}}}{\beta }{c_1} } = {\frac{2}{\beta }{c_2} - \sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{c_1} } = {\frac{2}{\beta }\sqrt[\large 3\normalsize]{{\alpha \beta }}{C_3} - \sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}\left( { - 2{C_3} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_2}} \right) } = {2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_3} + 2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_3} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_2} } = {4\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_3} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_2}.} \] В результате получаем решение однородной системы в виде \[ {I\left( t \right) = \left( {{a_0} + {a_1}t + {a_2}{t^2}} \right){e^{{\lambda _1}t}} } = {\left( {{C_1} + {C_2}t + {C_3}{t^2}} \right){e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}},} \] \[ {P\left( t \right) = \left( {{b_0} + {b_1}t + {b_2}{t^2}} \right){e^{{\lambda _1}t}} } = {\left[ {\left( { - \frac{2}{\beta }{C_3} + 2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_2} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_1}} \right)} \right. } + {\left( {4\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_3} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_2}} \right)t } - {\left. {\sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_3}{t^2}} \right]{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}},} \] \[ {S\left( t \right) = \left( {{c_0} + {c_1}t + {c_2}{t^2}} \right){e^{{\lambda _1}t}} } = {\left[ {\left( { - {C_2} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_1}} \right) + \left( { - 2{C_3} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_2}} \right)t} \right. } + {\left. {\sqrt[\large 3\normalsize]{{\alpha \beta }}{C_3}{t^2}} \right]{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}},} \] или в векторной записи: \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} {{C_1} + {C_2}t + {C_3}{t^2}}\\ { - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_1} + 2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_2} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_2}t - \frac{2}{\beta }{C_3} + 4\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}{C_3}t - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{C_3}{t^2}}\\ {\sqrt[\large 3\normalsize]{{\alpha \beta }}{C_1} - {C_2} + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_2}t - 2{C_3}t + \sqrt[\large 3\normalsize]{{\alpha \beta }}{C_3}{t^2}} \end{array}} \right) } = {{C_1}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} 1\\ { - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}}\\ {\sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) } + {{C_2}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} t\\ {2\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}} - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}t}\\ { - 1 + \sqrt[\large 3\normalsize]{{\alpha \beta }}t} \end{array}} \right) } + {{C_3}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} {{t^2}}\\ { - \frac{2}{\beta } + 4\sqrt[\large 3\normalsize]{{\frac{\alpha }{{{\beta ^2}}}}}t - \sqrt[\large 3\normalsize]{{\frac{{{\alpha ^2}}}{\beta }}}{t^2}}\\ { - 2t + \sqrt[\large 3\normalsize]{{\alpha \beta }}{t^2}} \end{array}} \right).} \] Выполним некоторые упрощения. Каждое слагаемое умножим на \({\large\frac{1}{\beta }\normalsize} \cdot \beta = 1,\) при этом параметр \(\beta\) внесем в координаты каждого вектора: \[ {\mathbf{Z}\left( t \right) = \frac{{{C_1}}}{\beta }{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} \beta \\ { - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}}\\ {\beta \sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) } + {\frac{{{C_2}}}{\beta }{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} {\beta t}\\ {2\sqrt[\large 3\normalsize]{{\alpha \beta }} - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}t}\\ { - \beta + \beta \sqrt[\large 3\normalsize]{{\alpha \beta }}t} \end{array}} \right) } + {\frac{{{C_3}}}{\beta }{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} {\beta {t^2}}\\ { - 2 + 4\sqrt[\large 3\normalsize]{{\alpha \beta }}t - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}{t^2}}\\ { - 2\beta t + \beta \sqrt[\large 3\normalsize]{{\alpha \beta }}{t^2}} \end{array}} \right).} \] Переобозначим произвольные коэффициенты \({C_1},\) \({C_2},\) \({C_3}\) следующим образом: \[\frac{{{C_1}}}{\beta } \to {C_1},\;\;\frac{{{C_2}}}{\beta } \to {C_2},\;\;\frac{{{C_3}}}{\beta } \to {C_3}.\] Тогда решение принимает вид: \[ {\mathbf{Z}\left( t \right) = {C_1}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left( {\begin{array}{*{20}{c}} \beta \\ { - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}}\\ {\beta \sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right) } + {{C_2}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left[ {\left( {\begin{array}{*{20}{c}} 0\\ {2\sqrt[\large 3\normalsize]{{\alpha \beta }}}\\ { - \beta } \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \beta \\ { - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}}\\ {\beta \sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right)t} \right] } + {{C_3}{e^{ - \sqrt[\large 3\normalsize]{{\alpha \beta }}t}}\left[ {\left( {\begin{array}{*{20}{r}} 0\\ { - 2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ {4\sqrt[\large 3\normalsize]{{\alpha \beta }}}\\ { - 2\beta } \end{array}} \right)t + \left( {\begin{array}{*{20}{c}} \beta \\ { - \sqrt[\large 3\normalsize]{{{{\left( {\alpha \beta } \right)}^2}}}}\\ {\beta \sqrt[\large 3\normalsize]{{\alpha \beta }}} \end{array}} \right){t^2}} \right].} \] Заметим, что полученное выражение содержит \(3\) линейно независимых вектора. Обозначив \({\sqrt[\large 3\normalsize]{{\alpha \beta }}} = k,\) запишем общее решение как \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{C_1}{e^{ - kt}}\left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right) } + {{C_2}{e^{ - kt}}\left[ {\left( {\begin{array}{*{20}{c}} 0\\ {2k}\\ { - \beta } \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right)t} \right] } + {{C_3}{e^{ - kt}}\left[ {\left( {\begin{array}{*{20}{r}} 0\\ { - 2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ {4k}\\ { - 2\beta } \end{array}} \right)t + \left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right){t^2}} \right].} \] Теперь построим частное решение неоднородной системы. Учитывая, что правая часть системы состоит из констант: \[\mathbf{F} = \left( {\begin{array}{*{20}{c}} q\\ { - \alpha {I^*}}\\ { - \beta {P^*}} \end{array}} \right),\] будем искать частное решение также в виде постоянных чисел: \[{\mathbf{Z}_1} = \left( {\begin{array}{*{20}{c}} {{I_1}}\\ {{P_1}}\\ {{S_1}} \end{array}} \right).\] Подставляем вместо \(I,\) \(P,\) \(S\) постоянные числа \({I_1},\) \({P_1},\) \({S_1}:\) \[ {\left\{ \begin{array}{l} \frac{{dI}}{{dt}} + S = q\\ \frac{{dP}}{{dt}} - \alpha I = - \alpha {I^*}\\ \frac{{dS}}{{dt}} - \beta P = - \beta {P^*} \end{array} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{S_1} = q}\\ { - \alpha {I_1} = - \alpha {I^*}}\\ { - \beta {P_1} = - \beta {P^*}} \end{array}} \right.,}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{S_1} = q}\\ {{I_1} = {I^*}}\\ {{P_1} = {P^*}} \end{array}} \right..} \] Получаем частное решение в виде \[{\mathbf{Z}_1} = \left( {\begin{array}{*{20}{c}} {{I_1}}\\ {{P_1}}\\ {{S_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right).\] Таким образом, мы построили общее решение исходной неоднородной системы, которое записывается как \[ {\mathbf{Z}\left( t \right) = {C_1}{e^{ - kt}}\left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right) } + {{C_2}{e^{ - kt}}\left[ {\left( {\begin{array}{*{20}{c}} 0\\ {2k}\\ { - \beta } \end{array}} \right) + \left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right)t} \right] } + {{C_3}{e^{ - kt}}\left[ {\left( {\begin{array}{*{20}{r}} 0\\ { - 2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ {4k}\\ { - 2\beta } \end{array}} \right)t + \left( {\begin{array}{*{20}{c}} \beta \\ { - {k^2}}\\ {\beta k} \end{array}} \right){t^2}} \right] } + {\left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right).} \] 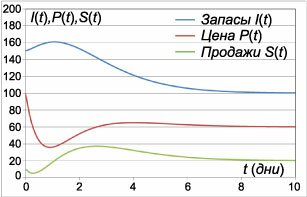Полученные выше формулы описывают поведение функций \(I\left( t \right),\) \(P\left( t \right),\) \(S\left( t \right)\) в зависимости от параметров задачи. Наша модель содержит пять параметров \(\alpha,\) \(\beta,\) \({{I^*}},\) \({{P^*}},\) \(q\) и три начальных значения переменных, которые обозначим как \({I_0},\) \({P_0},\) \({S_0}.\)

Далее рассмотрим случай, когда \(\alpha = \beta = -1.\) Тогда общее решение принимает такой вид: \[k = \sqrt[\large 3\normalsize]{{\alpha \beta }} = \sqrt[\large 3\normalsize]{1} = 1,\] \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{C_1}{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - 1}\\ { - 1}\\ { - 1} \end{array}} \right) } + {{C_2}{e^{ - t}}\left[ {\left( {\begin{array}{*{20}{c}} 0\\ 2\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - 1}\\ { - 1}\\ { - 1} \end{array}} \right)t} \right] } + {{C_3}{e^{ - t}}\left[ {\left( {\begin{array}{*{20}{r}} 0\\ { - 2}\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ 4\\ 2 \end{array}} \right)t + \left( {\begin{array}{*{20}{c}} { - 1}\\ { - 1}\\ { - 1} \end{array}} \right){t^2}} \right] + \left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right).} \] или \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - {C_1} - {C_2}t - {C_3}{t^2}}\\ { - {C_1} + {C_2}\left( {2 - t} \right) + {C_3}\left( { - 2 + 4t - {t^2}} \right)}\\ { - {C_1} + {C_2}\left( {1 - t} \right) + {C_3}\left( {2t - {t^2}} \right)} \end{array}} \right) } + {\left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right).} \] Константы \({C_1},\) \({C_2},\) \({C_3}\) определяются из начальных условий. В общем случае будем считать, что \[\mathbf{Z}\left( 0 \right) = \left( {\begin{array}{*{20}{c}} {I\left( 0 \right)}\\ {P\left( 0 \right)}\\ {S\left( 0 \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{I_0}}\\ {{P_0}}\\ {{S_0}} \end{array}} \right).\] Отсюда выразим постоянные \({C_1},\) \({C_2},\) \({C_3}:\) \[ {\left( {\begin{array}{*{20}{c}} { - {C_1}}\\ { - {C_1} + 2{C_2} - 2{C_3}}\\ { - {C_1} + {C_2}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{I_0}}\\ {{P_0}}\\ {{S_0}} \end{array}} \right),}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{C_1} = {I^*} - {I_0}}\\ {{C_2} = {S_0} - q + {I^*} - {I_0}}\\ {{C_3} = \frac{1}{2}\left( {{P^*} - {P_0} + {I^*} - {I_0}} \right) + {S_0} - q} \end{array}} \right..} \] Итак, решение для описанного случая выражается формулой \[ {\mathbf{Z}\left( t \right) = \left( {\begin{array}{*{20}{c}} {I\left( t \right)}\\ {P\left( t \right)}\\ {S\left( t \right)} \end{array}} \right) } = {{e^{ - t}}\left( {\begin{array}{*{20}{c}} { - {C_1} - {C_2}t - {C_3}{t^2}}\\ { - {C_1} + {C_2}\left( {2 - t} \right) + {C_3}\left( { - 2 + 4t - {t^2}} \right)}\\ { - {C_1} + {C_2}\left( {1 - t} \right) + {C_3}\left( {2t - {t^2}} \right)} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{I^*}}\\ {{P^*}}\\ q \end{array}} \right),}\;\; {\text{где}\;\;\left\{ {\begin{array}{*{20}{l}} {{C_1} = {I^*} - {I_0}}\\ {{C_2} = {S_0} - q + {I^*} - {I_0}}\\ {{C_3} = \frac{1}{2}\left( {{P^*} - {P_0} + {I^*} - {I_0}} \right) + {S_0} - q} \end{array}} \right..} \] Выше на рисунке \(2\) показаны типичные графики изменения запасов товара \({I\left( t \right)},\) цены \({P\left( t \right)}\) и объема продаж \({S\left( t \right)}.\) Данные кривые соответствуют следующей комбинации параметров: \(\alpha = \beta = 1,\) \({I^*} = 100,\) \({P^*} = 60,\) \(q = 20,\) \({I_0} = 150,\) \({P_0} = 100,\) \({S_0} = 10.\)

Из графиков видно, что после определенного переходного процесса все динамические величины приближаются к своим асимптотическим значениям, которые зависят от неоднородного компонента \(\mathbf{F}.\) Поскольку собственное значение \(\lambda\) отрицательно, то нулевое решение однородной системы является асимптотически устойчивым. Это приводит к тому, что однородная часть решения с течением времени "затухает", и функции \({I\left( t \right)},\) \({P\left( t \right)},\) \({S\left( t \right)}\) будут стремиться к асимптотическим значениям независимо от начальных условий. Таким образом, в рамках данной модели оказывается возможным поддерживать уровень запасов товара на определенном наперед заданном уровне, используя гибкий механизм изменения цены.