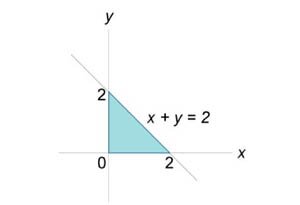Двойные интегралы в произвольной области

Пусть область интегрирования \(R\) типа \(I\) (элементарная относительно оси \(Oy\)) ограничена графиками функций \(x = a,\) \(x = b,\) \(y = p\left( x \right)\) и \(y = q\left( x \right).\) При этом выполняются неравенства \(a \lt b\) и \(p\left( x \right) \lt q\left( x \right)\) для всех \(x \in \left[ {a,b} \right].\) Тогда двойной интеграл по области \(R\) выражается через повторный по формуле \[ {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_{x = a}^{x = b} {\int\limits_{y = p\left( x \right)}^{y = q\left( x \right)} {f\left( {x,y} \right)dydx} } .} \] Аналогичное соотношение существует и для области типа \(II.\) Пусть область интегрирования \(R\) типа \(II\) (элементарная относительно оси \(Ox\)) ограничена графиками функций \(x = u\left( y \right),\) \(x = v\left( y \right),\) \(y = c,\) \(y = d\) при условии, что \(c \lt d\) и \(u\left( y \right) \lt v\left( y \right)\) для всех \(y \in \left[ {c,d} \right].\) Тогда двойной интеграл, заданный в области \(R,\) выражается через повторный интеграл по формуле \[ {\iint\limits_R {f\left( {x,y} \right)dxdy} } = {\int\limits_{y = c}^{y = d} {\int\limits_{x = u\left( y \right)}^{x = v\left( y \right)} {f\left( {x,y} \right)dxdy} } .} \] При решении задач иногда полезно разбить исходную область интегрирования \(R\) на две или более областей и вычислять двойной интеграл в каждой области отдельно.

   Пример 1

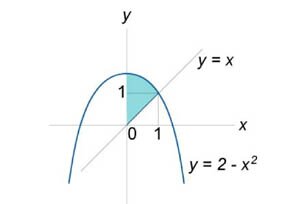
Вычислить интеграл \(\iint\limits_R {\left( {x - y} \right)dxdy}.\) Область интегрирования \(R\) ограничена графиками функций \(x = 0,\) \(x = 1,\) \(y = x,\) \(y = 2 - {x^2}.\) Область интегрирования \(R\) задана множеством \(R = \left\{ {\left( {x,y} \right)|\;0 \le x \le 1,x \le y \le 2 - {x^2}} \right\}\) и относится к типу \(I\) (рисунок \(1\)). Выразим двойной интеграл через повторный: \[ {\iint\limits_R {\left( {x - y} \right)dxdy} } = {\int\limits_0^1 {\int\limits_x^{2 - {x^2}} {\left( {x - y} \right)dydx} } } = {\int\limits_0^1 {\left[ {\int\limits_x^{2 - {x^2}} {\left( {x - y} \right)dy} } \right]dx} .} \] Вычислим сначала внутренний интеграл. \[ {\int\limits_x^{2 - {x^2}} {\left( {x - y} \right)dy} } = {\left. {\left( {xy - \frac{{{y^2}}}{2}} \right)} \right|_{y = x}^{2 - {x^2}} } = {\left[ {x\left( {2 - {x^2}} \right) - \frac{{{{\left( {2 - {x^2}} \right)}^2}}}{2}} \right] - \left[ {{x^2} - \frac{{{x^2}}}{2}} \right] } = { - \frac{{{x^4}}}{2} - {x^3} + \frac{{3{x^2}}}{2} + 2x - 2.} \] Теперь найдем внешний интеграл. \[ {\int\limits_0^1 {\left( { - \frac{{{x^4}}}{2} - {x^3} + \frac{{3{x^2}}}{2} + 2x - 2} \right)dx} } = {\left. {\left( { - \frac{{{x^5}}}{{10}} - \frac{{{x^4}}}{4} + \frac{{{x^3}}}{2} + {x^2} - 2x} \right)} \right|_0^1 } = { - \frac{{17}}{{20}}.} \]

   Пример 2

Вычислить интеграл \(\iint\limits_R {\left( {x + y} \right)dxdy} .\) Область интегрирования \(R\) ограничена прямыми \(x = 0,\) \(y = 0,\) \(x + y = 2.\) Область \(R\) представляется в виде множества \(R = \left\{ {\left( {x,y} \right)|\;0 \le x \le 2,0 \le y \le 2 - x} \right\}\) (рисунок \(2\)) и является областью \(I\) типа (элементарной относительно оси \(Oy\)). Преобразуя двойной интеграл в повторный, получаем: \[ {\iint\limits_R {\left( {x + y} \right)dxdy} } = {\int\limits_0^2 {\int\limits_0^{2 - x} {\left( {x + y} \right)dydx} } } = {\int\limits_0^2 {\left[ {\int\limits_0^{2 - x} {\left( {x + y} \right)dy} } \right]dx} } = {\int\limits_0^2 {\left[ {\left. {\left( {xy + \frac{{{y^2}}}{2}} \right)} \right|_{y = 0}^{2 - x}} \right]dx} } = {\int\limits_0^2 {\left[ {x\left( {2 - x} \right) + \frac{{{{\left( {2 - x} \right)}^2}}}{2}} \right]dx} } = {\int\limits_0^2 {\left( {2 - \frac{{{x^2}}}{2}} \right)dx} = \left. {\left( {2x - \frac{{{x^3}}}{6}} \right)} \right|_0^2 = \frac{8}{3}.} \]

   Пример 3

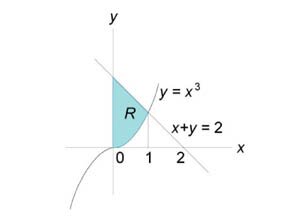
Вычислить интеграл \(\iint\limits_R {xdxdy},\) в котором область интегрирования \(R\) ограничена графиками функций \(y = {x^3},\) \(x + y = 2,\) \(x = 0.\) Область \(R\) показана ниже на рисунке \(3.\) Кривая \(y = {x^3}\) и линейная функция, заданная уравнением \(x + y = 2,\) пересекаются в точке \(\left( {1,1} \right).\) Следовательно, двойной интеграл равен \[ {\iint\limits_R {xdxdy} } = {\int\limits_0^1 {\int\limits_{{x^3}}^{2 - x} {xdydx} } } = {\int\limits_0^1 {\left[ {\int\limits_{{x^3}}^{2 - x} {xdy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left. {\left( {xy} \right)} \right|_{y = {x^3}}^{2 - x}} \right]dx} } = {\int\limits_0^1 {\left[ {x\left( {2 - x} \right) - {x^4}} \right]dx} } = {\left. {\left( {{x^2} - \frac{{{x^3}}}{3} - \frac{{{x^5}}}{5}} \right)} \right|_0^1 } = {1 - \frac{1}{3} - \frac{1}{5} = \frac{7}{{15}}.} \]

   Пример 4

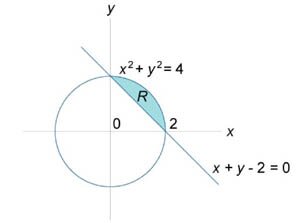
Найти интеграл \(\iint\limits_R {{x^2}ydxdy},\) где область \(R\) представляет собой сегмент окружности. Границы сегмента заданы уравнениями \({x^2} + {y^2} = 4,\) \(x + y - 2 = 0.\) Окружность \({x^2} + {y^2} = 4\) имеет радиус \(2\) и центр в начале координат. Область интегрирования показана на рисунке \(4.\) Поскольку верхняя полуокружность описывается уравнением \(y = \sqrt {4 - {x^2}},\) то двойной интеграл вычисляется следующим образом: \[ {\iint\limits_R {{x^2}ydxdy} } = {\int\limits_0^2 {\int\limits_{2 - x}^{\sqrt {4 - {x^2}} } {{x^2}ydxdy} } } = {\int\limits_0^2 {\left[ {\int\limits_{2 - x}^{\sqrt {4 - {x^2}} } {{x^2}ydy} } \right]dx} } = {\int\limits_0^2 {\left[ {\left. {\left( {\frac{{{x^2}{y^2}}}{2}} \right)} \right|_{y = 2 - x}^{\sqrt {4 - {x^2}} }} \right]dx} } = {\frac{1}{2}\int\limits_0^2 {\left[ {{x^2}\left( {4 - {x^2}} \right) - {x^2}{{\left( {2 - x} \right)}^2}} \right]dx} } = {\frac{1}{2}\int\limits_0^2 {\left[ {4{x^2} - {x^4} - {x^2}\left( {4 - 4x + {x^2}} \right)} \right]dx} } = {\frac{1}{2}\int\limits_0^2 {\left( {4{x^3} - 2{x^4}} \right)dx} } = {\frac{1}{2}\left. {\left( {{x^4} - \frac{{2{x^5}}}{5}} \right)} \right|_0^2 } = {\frac{1}{2}\left( {16 - \frac{{64}}{5}} \right) = \frac{8}{5}.} \]

   Пример 5

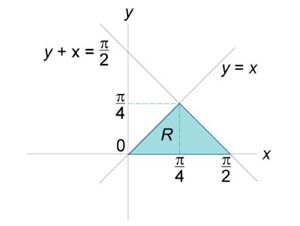
Найти интеграл \(\iint\limits_R {\sin \left( {x + y} \right)dxdy},\) заданный в области \(R,\) ограниченной прямыми \(y = x,\) \(x + y = \large\frac{\pi }{2}\normalsize,\) \(y = 0.\) Область интегрирования \(R\) показана ниже на рисунке \(5.\) Рассматривая ее как область типа \(II\) (элементарную относительно оси \(Ox,\) двойной интеграл можно преобразовать в повторный и вычислить следующим образом: \[ {\iint\limits_R {\sin \left( {x + y} \right)dxdy} } = {\int\limits_0^{\frac{\pi }{4}} {\left[ {\int\limits_0^{\frac{\pi }{2} - y} {\sin \left( {x + y} \right)dx} } \right]dy} } = {\int\limits_0^{\frac{\pi }{4}} {\left[ {\left. {\left( { - \cos \left( {x + y} \right)} \right)} \right|_{x = y}^{\frac{\pi }{2} - y}} \right]dy} } = { - \int\limits_0^{\frac{\pi }{4}} {\left[ {\cos \left( {\frac{\pi }{2} - y + y} \right) - \cos 2y} \right]dy} } = {\int\limits_0^{\frac{\pi }{4}} {\cos 2ydy} } = {\left. {\left( {\frac{{\sin 2y}}{2}} \right)} \right|_0^{\frac{\pi }{4}} } = {\frac{1}{2}\left( {\sin \frac{\pi }{2} - \sin 0} \right) = \frac{1}{2}.} \]

   Пример 6

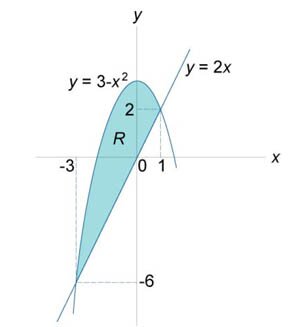
Найти интеграл \(\iint\limits_R {ydydx},\) где \(R\) ограничена прямой \(y = 2x\) и параболой \(y = 3 - {x^2}.\) Область интегрирования изображена выше на рисунке \(6.\) Найдем точки пересечения прямой и параболы. \[ {\left\{ \begin{array}{l} y = 2x\\ y = 3 - {x^2} \end{array} \right.,}\;\; {\Rightarrow 2x = 3 - {x^2},}\;\; {\Rightarrow {x^2} + 2x - 3 = 0,}\;\; {\Rightarrow {x_{1,2}} = \frac{{ - 2 \pm \sqrt {16} }}{2} = - 3;\;1.} \] Следовательно, линии, ограничивающие область \(R,\) пересекаются в точках \(\left( { - 3, - 6} \right)\) и \(\left( {1, 2} \right).\) Тогда исходный двойной интеграл равен \[ {\iint\limits_R {ydydx} } = {\int\limits_{ - 3}^1 {\left[ {\int\limits_{2x}^{3 - {x^2}} {ydy} } \right]dx} } = {\int\limits_{ - 3}^1 {\left[ {\left. {\left( {\frac{{{y^2}}}{2}} \right)} \right|_{y = 2x}^{3 - {x^2}}} \right]dx} } = {\frac{1}{2}\int\limits_{ - 3}^1 {\left[ {{{\left( {3 - {x^2}} \right)}^2} - {{\left( {2x} \right)}^2}} \right]dx} } = {\frac{1}{2}\int\limits_{ - 3}^1 {\left( {9 - 10{x^2} + {x^4}} \right)dx} } = {\frac{1}{2}\left. {\left( {9x - \frac{{10{x^3}}}{3} + \frac{{{x^5}}}{5}} \right)} \right|_{ - 3}^1 } = {\frac{1}{2}\left[ {\left( {9 - \frac{{10}}{3} + \frac{1}{5}} \right) - \left( { - 27 + \frac{{10 \cdot 27}}{3} - \frac{{243}}{5}} \right)} \right] } = { - \frac{{64}}{{15}}.} \]

   Пример 7

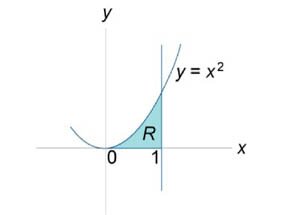
Найти интеграл \(\iint\limits_R {x\sin ydydx},\) где область \(R\) ограничена линиями \(y = 0,\) \(y = {x^2},\) \(x = 1.\) Область интегрирования описывается множеством \(R = \left\{ {\left( {x,y} \right)|\;0 \le x \le 1,0 \le y \le {x^2}} \right\}\) и показана ниже на рисунке \(7.\) Двойной интеграл равен \[ {I = \iint\limits_R {x\sin ydydx} } = {\int\limits_0^1 {\left[ {\int\limits_0^{{x^2}} {x\sin ydy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left. {\left( { - x\cos y} \right)} \right|_{y = 0}^{{x^2}}} \right]dx} } = {\int\limits_0^1 {\left( { - x\cos {x^2} + x\cos 0} \right)dx} } = {\int\limits_0^1 {\left( {1 - \cos {x^2}} \right)xdx} .} \] Для вычисления последнего интеграла сделаем замену \[ {z = {x^2},}\;\; {\Rightarrow dz = 2xdx,}\;\; {\Rightarrow xdx = \frac{{dz}}{2}.} \] Если \(x = 0,\) то \(x = 0.\) Соответственно, при \(x = 1\) имеем \(z = 1.\) Тогда интеграл легко вычисляется: \[ {I = \int\limits_0^1 {\left( {1 - \cos {x^2}} \right)xdx} } = {\int\limits_0^1 {\left( {1 - \cos z} \right)\frac{{dz}}{2}} } = {\frac{1}{2}\int\limits_0^1 {\left( {1 - \cos z} \right)dz} } = {\frac{1}{2}\left. {\left( {z - \sin z} \right)} \right|_0^1 } = {\frac{{1 - \sin 1}}{2} \approx 0,08.} \]

   Пример 8

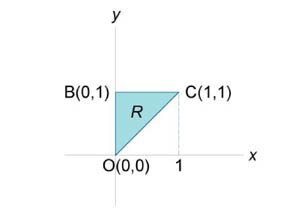
Вычислить интеграл \(\iint\limits_R {{e^x}dxdy}.\) Область интегрирования представляет собой треугольник с вершинами \(O\left( {0,0} \right),\) \(B\left( {0,1} \right),\) и \(C\left( {1,1} \right).\) Область \(R\) показана выше на рисунке \(8.\) Очевидно, уравнение стороны треугольника \(OC\) имеет вид \(y = x,\) а уравнение стороны \(BC\) равно \(y = 1.\) Рассматривая \(R\) как область типа \(I,\) получаем \[ {I = \iint\limits_R {{e^x}dxdy} } = {\int\limits_0^1 {\left[ {\int\limits_x^1 {{e^x}dy} } \right]dx} } = {\int\limits_0^1 {\left[ {\left. {\left( {{e^x}y} \right)} \right|_{y = x}^1} \right]dx} } = {\int\limits_0^1 {\left( {{e^x} - x{e^x}} \right)dx} } = {\int\limits_0^1 {{e^x}\left( {1 - x} \right)dx} .} \] Полученный внешний интеграл вычислим с помощью интегрирования по частям. Пусть \(u = 1 - x,\) \(dv = {e^x}dx.\) Тогда \(du = -dx,\) \(v = \int {{e^x}dx} = {e^x}.\) Следовательно, \[ {I = \int\limits_0^1 {{e^x}\left( {1 - x} \right)dx} } = {\left. {\left[ {{e^x}\left( {1 - x} \right)} \right]} \right|_0^1 + \int\limits_0^1 {{e^x}dx} } = {\left. {\left[ {{e^x}\left( {1 - x} \right)} \right]} \right|_0^1 + \left. {\left[ {{e^x}} \right]} \right|_0^1 } = {\left. {\left[ {2{e^x} - x{e^x}} \right]} \right|_0^1 } = {2e - e - 2 = e - 2.} \]

   Пример 9

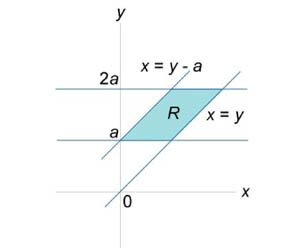
Вычислить интеграл \(\iint\limits_R {\left( {x + y} \right)dxdy},\) где область \(R\) представляет собой параллелограмм со сторонами \(y = x,\) \(y = x + a,\) \(y = a,\) \(y = 2a,\) \(a\) − некоторый параметр. Будем рассматривать \(R\) как область типа \(II\) (элементарную относительно оси \(Ox\)). Схематически она изображена внизу на рисунке \(9.\) При изменении координаты \(y\) от \(a\) до \(2a\) координата \(x\) принимает значения между \(x = y - a\) и \(x = y.\) Поэтому двойной интеграл равен \[ {\iint\limits_R {\left( {x + y} \right)dxdy} } = {\int\limits_a^{2a} {\left[ {\int\limits_{y - a}^y {\left( {x + y} \right)dx} } \right]dy} } = {\int\limits_a^{2a} {\left[ {\left. {\left( {\frac{{{x^2}}}{2} + yx} \right)} \right|_{x = y - a}^y} \right]dy} } = {\int\limits_a^{2a} {\left[ {\left( {\frac{{{y^2}}}{2} + {y^2}} \right) - \left( {\frac{{{{\left( {y - a} \right)}^2}}}{2} + y\left( {y - a} \right)} \right)} \right]dy} } = {\int\limits_a^{2a} {\left( {\frac{{3{y^2}}}{2} - \frac{{{y^2} - 2ay + {a^2}}}{2} - {y^2} + ay} \right)dy} } = {\int\limits_a^{2a} {\left( {2ay - \frac{{{a^2}}}{2}} \right)dy} } = {\left. {\left( {\frac{{2a{y^2}}}{2} - \frac{{{a^2}y}}{2}} \right)} \right|_a^{2a} } = {\left. {\left( {a{y^2} - \frac{{{a^2}y}}{2}} \right)} \right|_a^{2a} } = {\left( {a \cdot {{\left( {2a} \right)}^2} - \frac{{{a^2}}}{2} \cdot 2a} \right) - \left( {a \cdot {a^2} - \frac{{{a^2}}}{2} \cdot a} \right) } = {4{a^3} - {a^3} - {a^3} + \frac{{{a^3}}}{2} = \frac{{5{a^3}}}{2}.} \]