Геометрические приложения поверхностных интегралов

С помощью поверхностных интегралов вычисляются

• Площадь поверхности;

• Объем тела, ограниченного замкнутой поверхностью.

Пусть \(S\) является гладкой, кусочно-непрерывной поверхностью. Площадь поверхности определяется интегралом \[A = \iint\limits_S {dS} .\] Если поверхность \(S\) задана параметрически с помощью вектора \[ {\mathbf{r}\left( {u,v} \right) } = {x\left( {u,v} \right)\mathbf{i} + y\left( {u,v} \right)\mathbf{j} + z\left( {u,v} \right)\mathbf{k},} \] то площадь поверхности будет равна \[A = \iint\limits_{D\left( {u,v} \right)} {\left| {\frac{{\partial \mathbf{r}}}{{\partial u}} \times \frac{{\partial \mathbf{r}}}{{\partial v}}} \right|dudv} ,\] где \({D\left( {u,v} \right)}\) − это область, в которой задана поверхность.

Если поверхность \(S\) задана в явном виде функцией \({z\left( {x,y} \right)},\) то площадь поверхности выражается формулой \[A = \iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} ,\] где \({D\left( {x,y} \right)}\) − проекция поверхности \(S\) на плоскость \(Oxy.\) Предположим, что тело ограничено некоторой гладкой, замкнутой поверхностью \(S.\) Тогда объем тела определяется по формуле \[V = \frac{1}{3}\left| {\iint\limits_S {xdydz + ydxdz + zdxdy} } \right|.\]

   Пример 1

Вычислить площадь поверхности части параболоида \(z = 25 - {x^2} - {y^2},\) лежащей выше плоскости \(Oxy.\) Площадь заданной поверхности равна \[ {A = \iint\limits_S {dS} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial y}}} \right)}^2}} dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {1 + {{\left( {\frac{{ - x}}{{\sqrt {25 - {x^2} - {y^2}} }}} \right)}^2} + {{\left( {\frac{{ - y}}{{\sqrt {25 - {x^2} - {y^2}} }}} \right)}^2}} dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {\frac{{5dxdy}}{{\sqrt {25 - {x^2} - {y^2}} }}} .} \] Переходя к полярным координатам, находим ответ: \[ {A = \int\limits_0^{2\pi } {d\varphi } \int\limits_0^5 {\frac{{5rdr}}{{\sqrt {25 - {r^2}} }}} } = {10\pi \int\limits_0^5 {\frac{{rdr}}{{\sqrt {25 - {r^2}} }}} } = { - 5\pi \int\limits_0^5 {\frac{{d\left( {25 - {r^2}} \right)}}{{\sqrt {25 - {r^2}} }}} } = { - 5\pi \left[ {\left. {\left( {\frac{{\sqrt {25 - {r^2}} }}{{\frac{1}{2}}}} \right)} \right|_0^5} \right] } = {50\pi .} \]

   Пример 2

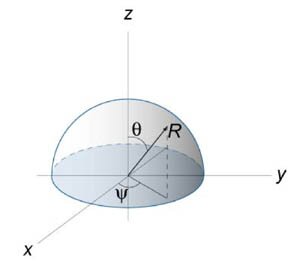
Найти площадь полусферы радиуса \(R.\) В сферических координатах поверхность верхней полусферы описывается в виде \[ {\mathbf{r}\left( {\psi ,\theta } \right) } = {R\cos \psi \sin \theta \cdot \mathbf{i} + R\sin \psi \sin \theta \cdot \mathbf{j} + R\cos \theta \cdot \mathbf{k},} \] где \(0 \le \psi \le 2\pi ,\) \(0 \le \theta \le \large\frac{\pi }{2}\normalsize\) (рисунок \(1\)).
Вычислим дифференциальный элемент площади. \[ {\frac{{\partial \mathbf{r}}}{{\partial \psi }} } = {\frac{\partial }{{\partial \psi }}\left( {R\cos \psi \sin \theta ,R\sin \psi \sin \theta ,R\cos \theta } \right) } = {\left( { - R\sin \psi \sin \theta ,R\cos \psi \sin \theta ,0} \right);} \] \[ {\frac{{\partial \mathbf{r}}}{{\partial \theta }} } = {\frac{\partial }{{\partial \theta }}\left( {R\cos \psi \sin \theta ,R\sin \psi \sin \theta ,R\cos \theta } \right) } = {\left( {R\cos \psi \cos \theta ,R\sin \psi \cos \theta , - R\sin \theta } \right).} \] Найдем векторное произведение данных векторов: \[ {\frac{{\partial \mathbf{r}}}{{\partial \psi }} \times \frac{{\partial \mathbf{r}}}{{\partial \theta }} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ { - R\sin \psi \sin \theta } & {R\cos \psi \sin \theta } & 0\\ {R\cos \psi \cos \theta }&{R\sin \psi \cos \theta }&{ - R\sin \theta } \end{array}} \right| } = { - {R^2}\cos \psi \,{\sin ^2}\theta \cdot \mathbf{i} } - {{R^2}\sin\psi \,{\sin ^2}\theta \cdot \mathbf{j} } - {{R^2}\left( {{\sin^2}\psi \sin \theta \cos \theta + {{\cos }^2}\psi \sin \theta \cos \theta } \right) \cdot \mathbf{k} } = { - {R^2}\cos \psi \,{\sin ^2}\theta \cdot \mathbf{i} } - {{R^2}\sin\psi \,{\sin ^2}\theta \cdot \mathbf{j} } - {{R^2}\sin \theta \cos \theta \cdot \mathbf{k}.} \] Следовательно, элемент площади будет равен \[ {dS = \left| {\frac{{\partial \mathbf{r}}}{{\partial \psi }} \times \frac{{\partial \mathbf{r}}}{{\partial \theta }}} \right|d\psi d\theta } = {\sqrt {{{\left( { - {R^2}\cos \psi \,{{\sin }^2}\theta } \right)}^2} + {{\left( { - {R^2}\sin\psi \,{{\sin }^2}\theta } \right)}^2} + {{\left( { - {R^2}\sin \theta \cos \theta } \right)}^2}} d\psi d\theta } = {{R^2}\sqrt {{{\sin }^4}\theta \left( {{{\cos }^2}\psi + {{\sin }^2}\psi } \right) + {{\sin }^2}\theta \,{{\cos }^2}\theta } d\psi d\theta } = {{R^2}\sin \theta \sqrt {{{\sin }^2}\theta + {{\cos }^2}\theta } d\psi d\theta } = {{R^2}\sin \theta d\psi d\theta .} \] Отсюда вычисляем площадь полусферы: \[ {A = \iint\limits_S {dS} } = {\int\limits_{D\left( {\psi ,\theta } \right)} {{R^2}\sin \theta d\psi d\theta } } = {{R^2}\int\limits_0^{2\pi } {d\psi } \int\limits_0^{\large\frac{\pi }{2}\normalsize} {\sin \theta d\theta } } = {2\pi {R^2} \cdot \left[ {\left. {\left( { - \cos \theta } \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } = {2\pi {R^2}\left( { - \cos \frac{\pi }{2} + \cos 0} \right) } = {2\pi {R^2}.} \]

   Пример 3

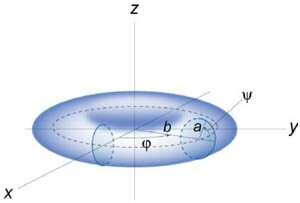
Вычислить площадь поверхности тора, заданного уравнением \({z^2} + {\left( {r - b} \right)^2} = {a^2}\;\;\left( {0 \le a \le b} \right)\) в цилиндрических координатах. Параметрические уравнения тора имеют вид (рисунок \(2\)): \[\left\{ \begin{array}{l} x = \left( {b + a\cos \psi } \right)\cos \varphi \\ y = \left( {b + a\cos \psi } \right)\sin\varphi \\ z = a\sin \psi \end{array} \right..\] Убедимся, что эти уравнения правильно описывают окружность в сечении тора. Действительно, поскольку \({x^2} + {y^2} = {r^2},\) то после подстановки получаем \[ {{\left( {b + a\cos \psi } \right)^2}{\cos ^2}\varphi + {\left( {b + a\cos \psi } \right)^2}{\sin^2}\varphi = {r^2},}\;\; {\Rightarrow {\left( {b + a\cos \psi } \right)^2} = {r^2},}\;\; {\Rightarrow r = b + a\cos \psi ,}\;\; {\Rightarrow r - b = a\cos \psi ,}\;\; {\Rightarrow {\left( {r - b} \right)^2} + {z^2} = {\left( {a\cos \psi } \right)^2} + {\left( {a\sin \psi } \right)^2},}\;\; {\Rightarrow {\left( {r - b} \right)^2} + {z^2} = {a^2}.} \] Таким образом, поверхность тора описывается следующим вектором: \[ \mathbf{r}\left( {\varphi ,\psi } \right) = \left( {b + a\cos \psi } \right)\cos \varphi \cdot \mathbf{i} + \left( {b + a\cos \psi } \right)\sin\varphi \cdot \mathbf{j} + a\sin \psi \cdot \mathbf{k}. \] Для вычисления площади поверхности воспользуемся формулой \[ {A = \iint\limits_S {dS} } = {\iint\limits_{D\left( {\varphi ,\psi } \right)} {\left| {\frac{{\partial \mathbf{r}}}{{\partial \varphi }} \times \frac{{\partial \mathbf{r}}}{{\partial \psi }}} \right|d\varphi d\psi } .} \] Входящее в эту формулу векторное произведение имеет вид \[ \frac{{\partial \mathbf{r}}}{{\partial \varphi }} \times \frac{{\partial \mathbf{r}}}{{\partial \psi }} = \left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ { - \left( {b + a\cos \psi } \right)\sin \varphi } & {\left( {b + a\cos \psi } \right)\cos\varphi } & 0\\ { - a\sin \psi \cos \varphi } & { - a\sin \psi \sin \varphi } & {a\cos\psi } \end{array}} \right| = a\cos\psi \left( {b + a\cos \psi } \right)\cos\varphi \cdot \mathbf{i} + a\cos\psi \left( {b + a\cos \psi } \right)\sin\varphi \cdot \mathbf{j} + \left[ {a\sin \psi \,{{\sin }^2}\varphi \left( {b + a\cos \psi } \right) + a\sin \psi \,{{\cos }^2}\varphi \left( {b + a\cos \psi } \right)} \right] \cdot \mathbf{k} = a\cos\varphi \cos \psi \left( {b + a\cos \psi } \right) \cdot \mathbf{i} + a\sin\varphi \cos \psi \left( {b + a\cos \psi } \right) \cdot \mathbf{j} + a\sin\psi \left( {b + a\cos \psi } \right) \cdot \mathbf{k}. \] Тогда модуль векторного произведения равен \[ {\left| {\frac{{\partial \mathbf{r}}}{{\partial \varphi }} \times \frac{{\partial \mathbf{r}}}{{\partial \psi }}} \right| } = {\left[ {{a^2}{\cos^2}\varphi \,{{\cos }^2}\psi {{\left( {b + a\cos \psi } \right)}^2}} \right. } + {{a^2}{\sin^2}\varphi \,{\cos ^2}\psi {\left( {b + a\cos \psi } \right)^2} } + {{\left. {{a^2}{{\sin }^2}\psi {{\left( {b + a\cos \psi } \right)}^2}} \right]^{\large\frac{1}{2}\normalsize}} } = {a{\left[ {{{\cos }^2}\psi {{\left( {b + a\cos \psi } \right)}^2} + {{\sin }^2}\psi {{\left( {b + a\cos \psi } \right)}^2}} \right]^{\large\frac{1}{2}\normalsize}} } = {a\left( {b + a\cos \psi } \right).} \] Отсюда находим площадь поверхности тора: \[ {A = \iint\limits_S {dS} } = {\iint\limits_{D\left( {\varphi ,\psi } \right)} {a\left( {b + a\cos \psi } \right)d\varphi d\psi } } = {a\int\limits_0^{2\pi } {d\varphi } \int\limits_0^{2\pi } {\left( {b + a\cos \psi } \right)d\psi } } = {2\pi a\int\limits_0^{2\pi } {\left( {b + a\cos \psi } \right)d\psi } } = {2\pi a\left[ {\left. {\left( {b\psi + a\sin \psi } \right)} \right|_0^{2\pi }} \right] } = {2\pi a \cdot 2\pi b } = {4{\pi ^2}ab.} \]

   Пример 4

Вычислить объем эллипсоида \(\large\frac{{{x^2}}}{{{a^2}}}\normalsize + \large\frac{{{y^2}}}{{{b^2}}}\normalsize + \large\frac{{{z^2}}}{{{c^2}}}\normalsize = 1.\) Для нахождения объема используем формулу \[V = \frac{1}{3}\left| {\iint\limits_S {xdydz + ydxdz + zdxdy} } \right|.\] Поверхность эллипсоида можно представить в параметрической форме следующим образом: \[ {\mathbf{r}\left( {u,v} \right) } = {a\cos u\sin v \cdot \mathbf{i} + b\sin u\sin v \cdot \mathbf{j} + c\cos v \cdot \mathbf{k},\;\;\text{где} }\;\; {0 \le u \le 2\pi ,}\;\; {0 \le v \le \pi .} \] (Переменные \(u, v\) соответствуют сферическим координатам \(\psi\) и \(\theta\).)
В формуле для объема векторное поле имеет координаты \(\mathbf{F} = \left( {x,y,z} \right),\) поэтому \[ {P = x = a\cos u\sin v,}\;\; {Q = y = b\sin u\sin v,}\;\; {R = z = c\cos v.} \] Поскольку \[ {\iint\limits_S {Pdydz + Qdzdx + Rdxdy} } = {\iint\limits_{D\left( {u,v} \right)} {\left| {\begin{array}{*{20}{c}} P & Q & R\\ {\frac{{\partial x}}{{\partial u}}}&{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial z}}{{\partial u}}}\\ {\frac{{\partial x}}{{\partial v}}}&{\frac{{\partial y}}{{\partial v}}}&{\frac{{\partial z}}{{\partial v}}} \end{array}} \right|dudv} ,} \] то получаем следующее выражение для поверхностного интеграла: \[ {\iint\limits_S {xdydz + ydzdx + zdxdy} } = {\iint\limits_{D\left( {u,v} \right)} {\left| {\begin{array}{*{20}{c}} {a\cos u\sin v}&{b\sin u\sin v}&{c\cos v}\\ { - a\sin u\sin v}&{b\cos u\sin v}&0\\ {a\cos ucosv}&{b\sin u\cos v}&{ - c\sin v} \end{array}} \right|dudv} } = {\int\limits_{D\left( {u,v} \right)} {\left[ {a\cos u\sin v\left( { - bc\cos u\,{{\sin }^2}v} \right)} \right.} } - {b\sin u\sin v\left( {ac\sin u\,{{\sin }^2}v} \right) } + {\left. {c\cos v\left( { - ab\,{{\sin }^2}u\sin v\cos v - ab\,{{\cos }^2}u\sin v\cos v} \right)} \right]dudv } = {\iint\limits_{D\left( {u,v} \right)} {\left[ { - abc\,{{\cos }^2}u\,{{\sin }^3}v } - {abc\,{{\sin }^2}u\,{{\sin }^3}v} \right.} \left. { - abc\sin v\,{{\cos }^2}v\left( {{{\sin }^2}u } + {{{\cos }^2}u} \right)} \right]dudv } = { - abc\iint\limits_{D\left( {u,v} \right)} {\left[ {{{\sin }^3}v\left( {{{\cos }^2}u + {{\sin }^2}u} \right) + \sin v\,{{\cos }^2}v} \right]dudv} } = { - abc\iint\limits_{D\left( {u,v} \right)} {\sin v\left( {{{\sin }^2}v + {{\cos }^2}v} \right)dudv} } = { - abc\iint\limits_{D\left( {u,v} \right)} {\sin v dudv} } = { - abc\iint\limits_0^{2\pi } {du} \int\limits_0^\pi {\sin v dv} } = { - abc \cdot 2\pi \cdot \left. {\left( { - \cos v} \right)} \right|_0^\pi } = {2\pi abc \cdot \left( {\cos \pi - \cos 0} \right) } = { - 4\pi abc.} \] Следовательно, объем эллипсоида равен \[V = \left| {\frac{1}{3}\left( { - 4\pi abc} \right)} \right| = \frac{{4\pi abc}}{3}.\]